- 2021-04-16 发布 |
- 37.5 KB |
- 3页
申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2019七年级数学下册 7三角形的内角和
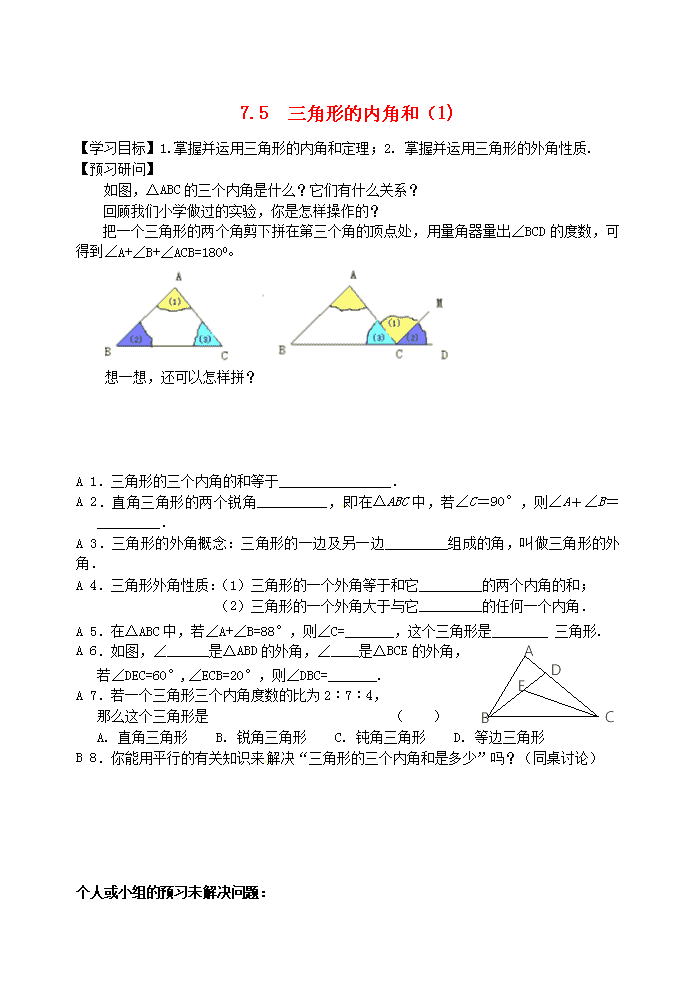
7.5 三角形的内角和(1) 【学习目标】1.掌握并运用三角形的内角和定理;2. 掌握并运用三角形的外角性质. 【预习研问】 如图,△ABC的三个内角是什么?它们有什么关系? 回顾我们小学做过的实验,你是怎样操作的? 把一个三角形的两个角剪下拼在第三个角的顶点处,用量角器量出∠BCD的度数,可得到∠A+∠B+∠ACB=1800。 想一想,还可以怎样拼? A 1.三角形的三个内角的和等于________________. A 2.直角三角形的两个锐角__________,即在△ABC中,若∠C=90°,则∠A+∠B=_________. A 3.三角形的外角概念:三角形的一边及另一边_________组成的角,叫做三角形的外角. A 4.三角形外角性质:(1)三角形的一个外角等于和它_________的两个内角的和; (2)三角形的一个外角大于与它_________的任何一个内角. A D C B E A 5.在△ABC中,若∠A+∠B=88°,则∠C=_______,这个三角形是________ 三角形. A 6.如图,∠______是△ABD的外角,∠____是△BCE的外角, 若∠DEC=60°,∠ECB=20°,则∠DBC=_______. A 7.若一个三角形三个内角度数的比为2︰7︰4, 那么这个三角形是 ( ) A. 直角三角形 B. 锐角三角形 C. 钝角三角形 D. 等边三角形 B 8.你能用平行的有关知识来解决“三角形的三个内角和是多少”吗?(同桌讨论) 个人或小组的预习未解决问题: 【课内解问】 A 1.在△ABC中,若∠A=2∠B=3∠C,则△ABC的形状为 ( ) A.锐角三角形 B.直角三角形 C.钝角三角形 D.等边三角形 B 2.如图1,在△ABC中,若∠C=90°,EF∥AB,∠1=50°,则∠B的度数为( ) A.30° B.40° C.50° D.60° 图1 图1 1 2 3 图2 图3 图4 30° 45° A 3.如图2,将三角尺的直角顶点放在直尺的一边上,∠1=30°,∠2=50°,则∠3的度数等于 ( ) A.50° B.30° C.20° D.15° A 4.如图3,△ABC中,∠A=70°,∠B=60°,点D在BC的延长线上,则∠ACD等于( ) A.100° B.120° C.130° D.150° B 5.数学活动课上,小周将一副三角板按图4方式叠放,则∠等于( ) A.30° B.45° C.60° D.75° B 6.如图5,在△ABC中,∠AOB=135°,∠C=65°,则∠OBC+∠OAC=______°. 图5 A B G F C D E 1 2 图6 B 7. 如图6,将△ABC沿着DE翻折,若∠1+∠2=80O,则∠B=_____________. C 8. 在△ABC中,∠B=∠C,有一个角为70°,求另外两个角的度数. B 9.如图7,BD是△ABC的角平分线,∠A=40°,∠ABD=35°,求∠C和∠CDB的度数. 图7 【课后答问】 A 1.在一个三角形,若,则是 ( ) A.直角三角形 B.锐角三角形 C.钝角三角形 D.以上都不对 A 2.一个三角形的三个内角中,至少有 ( ) A. 一个锐角 B. 两个锐角 C. 一个钝角 D .一个直角 A 3.在△ABC中,∠A=55°,∠B比∠C大25°,则∠B的度数为( ) A. 50° B.75° C. 100° D. 125° A 4.三角形的一个外角小于和它相邻的内角,则此三角形是 ( ) A.锐角三角形 B.直角三角形 C.钝角三角形 D.不能确定 B 5.将一副常规的三角尺按如图方式放置,则图中∠AOB的度数为( ) A.75° B.95° C.105° D.120° B 6.△ABC中,∠A = 60°,∠B︰∠C = 1︰5. 求∠B的度数. C 7.认真阅读下面关于三角形内外角平分线所夹角的探究片段,完成相关问题. 探究1:如图11-1,在△ABC中,O是∠ABC与∠ACB的平分线BO和CO的交点,通过分析发现 .(只写结论,不需证明) 探究2:如图11-2中,O是∠ABC与外角∠ACD的平分线BO和CO的交点,试分析∠BOC与∠A有怎样的关系?请说明理由. 探究3:如图11-3中,O是外角∠DBC与外角∠ECB的平分线BO和CO的交点,则∠BOC与∠A有怎样的关系?(只写结论,不需证明) 结论: .查看更多