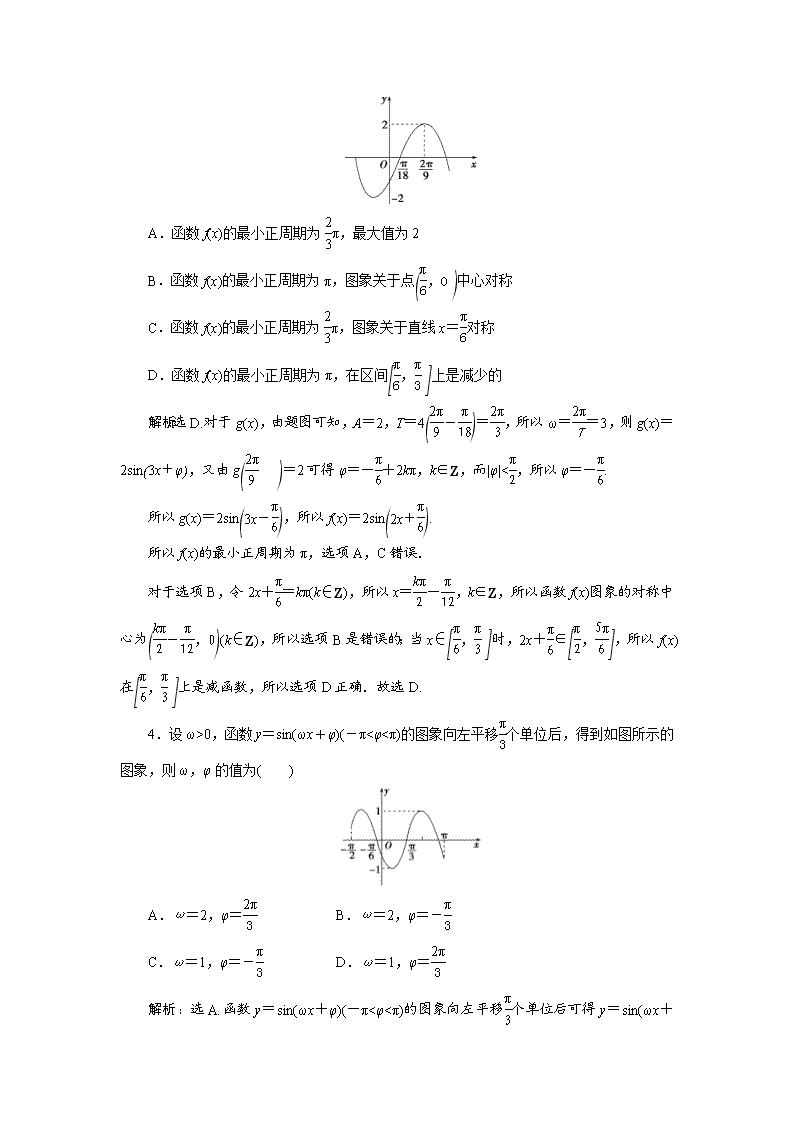高考理科数一轮复习高效演练分层突破:第四章 第5讲 函数y=Asin(ωx+φ)的图象及三角函数模型的简单应用
[基础题组练]
1.(2020·安徽蚌埠第二次数学质量检查)将函数f(x)=sin x+cos x的图象上各点的纵坐标不变,横坐标缩小为原来的,再将函数的图象向左平移个单位后,得到的函数g(x)的解析式为( )
A.g(x)=sin B.g(x)=sin
C.g(x)=sin D.g(x)=sin
解析:选B.f(x)=sin x+cos x=sin的图象y= sin的图象g(x)=sin=sin.故选B.
2.(2020·江西吉安期末教学质量检测)在平面直角坐标系xOy中,将函数f(x)=sin的图象向左平移φ(φ>0)个单位后得到的图象经过原点,则φ的最小值为( )
A. B.
C. D.
解析:选B.将函数f(x)=sin的图象向左平移φ(φ>0)个单位后得到的图象对应的解析式为y=sin[3(x+φ)+],因为其图象经过原点,所以sin=0,所以3φ+=kπ,k∈Z,解得φ=-,k∈Z,又φ>0,
所以φ的最小值为-=,故选B.
3.(2020·湖南衡阳高中毕业联考(二))将函数f(x)的图象向右平移个单位长度,再将所得函数图象上的所有点的横坐标缩短到原来的,得到函数g(x)=Asin(ωx+φ)的图象.已知函数g(x)的部分图象如图所示,则( )
A.函数f(x)的最小正周期为π,最大值为2
B.函数f(x)的最小正周期为π,图象关于点中心对称
C.函数f(x)的最小正周期为π,图象关于直线x=对称
D.函数f(x)的最小正周期为π,在区间上是减少的
解析:选D.对于g(x),由题图可知,A=2,T=4=,所以ω==3,则g(x)=2sin,又由g=2可得φ=-+2kπ,k∈Z,而|φ|<,所以φ=-.
所以g(x)=2sin,所以f(x)=2sin.
所以f(x)的最小正周期为π,选项A,C错误.
对于选项B,令2x+=kπ(k∈Z),所以x=-,k∈Z,所以函数f(x)图象的对称中心为(k∈Z),所以选项B是错误的;当x∈时,2x+∈,所以f(x)在上是减函数,所以选项D正确.故选D.
4.设ω>0,函数y=sin(ωx+φ)(-π<φ<π)的图象向左平移个单位后,得到如图所示的图象,则ω,φ的值为( )
A.ω=2,φ= B.ω=2,φ=-
C.ω=1,φ=- D.ω=1,φ=
解析:选A.函数y=sin(ωx+φ)(-π<φ<π)的图象向左平移个单位后可得y=sin(ωx+
eq f(πω,3)+φ).由函数的图象可知,=-(-)=,所以T=π.根据周期公式可得ω=2,所以y=sin(2x+φ+).由图知当y=-1时,x=×(-)=,所以函数的图象过(,-1),
所以sin(+φ)=-1.因为-π<φ<π,所以φ=.
故选A.
5.(2020·河南名校联盟联合调研)将函数g(x)=2sin x+1的图象向左平移个单位,再将所得图象上所有点的横坐标变为原来的(纵坐标不变),得到函数f(x)的图象,若f(x1)=f(x2)=3,且-π≤x2
0,ω>0,0<φ<π)的部分图象如图所示,已知x1,x2∈(,π),x1≠x2,且f(x1)=f(x2),则f(x1+x2)=________.
解析:由题意可得A=2,T=×=-=π,所以ω=2.
当x=时,f(x)=2,则ωx+φ=2×+φ=2kπ+,k∈Z,
据此可得φ=2kπ+(k∈Z),因为0<φ<π,令k=0可得φ=,则f(x)=2sin(2x+).当x∈(,π)时,<2x+<,所以f(x)在此区间上的对称轴方程为x=.由x1,x2∈(,π),x1≠x2,且f(x1)=f(x2),可得x1+x2=,
则f()=2sin(2×+)=2sin=2×=1.
答案:1
7.函数y=cos(2x+φ)(0<φ<π)的图象向右平移个单位后,与函数y=sin的图象重合,则φ=________.
解析:把函数y=cos (2x+φ)(0<φ<π)的图象向右平移个单位后,得到y=cos (2x-π+φ)的图象,
与函数y=sin的图象重合,则cos (2x-π+φ)=sin,即sin=sin,
所以-+φ=-,则φ=,
答案:
8.(2020·武汉调研)函数f(x)=Acos(ωx+φ)(ω>0)的部分图象如图所示,给出以下结论:
①f(x)的最小正周期为2;
②f(x)图象的一条对称轴为直线x=-;
③f(x)在(2k-,2k+),k∈Z上是减函数;
④f(x)的最大值为A.
则正确的结论为________.(填序号)
解析:由题图可知,函数f(x)的最小正周期T=2×(-)=2,故①正确;因为函数f(x)的图象过点(,0)和(,0),所以函数f(x)图象的对称轴为直线x=(+)+=+k(k∈Z),故直线x=-不是函数f(x)图象的对称轴,故②不正确;由图可知,当-+kT≤x≤++kT(k∈Z),即2k-≤x≤2k+(k∈Z)时,f(x)是减函数,故③正确;若A>0,则最大值是A,若A<0,则最大值是-A,故④不正确.
答案:①③
9.已知函数y=Asin(ωx+φ)(A>0,ω>0,|φ|<)的图象过点P(,0),图象上与点P
最近的一个最高点是Q(,5).
(1)求函数的解析式;
(2)求函数f(x)的增区间.
解:(1)依题意得A=5,
周期T=4(-)=π,
所以ω==2.
故y=5sin(2x+φ),
又图象过点P(,0),
所以5sin(+φ)=0,
由已知可得+φ=kπ,k∈Z,
因为|φ|<,所以φ=-,
所以y=5sin(2x-).
(2)由-+2kπ≤2x-≤+2kπ,k∈Z,得-+kπ≤x≤+kπ,k∈Z,
故函数f(x)的增区间为[kπ-,kπ+](k∈Z).
10.(2020·济南模拟)已知函数f(x)=sin ωxcos ωx+cos2ωx+b+1.
(1)若函数f(x)的图象关于直线x=对称,且ω∈[0,3],求函数f(x)的增区间;
(2)在(1)的条件下,当x∈[0,]时,函数f(x)有且只有一个零点,求实数b的取值范围.
解:(1)函数f(x)=sin ωxcos ωx+cos2ωx+b+1
=sin 2ωx++b+1=sin(2ωx+)++b.
因为函数f(x)的图象关于直线x=对称,所以2ω·+=kπ+,k∈Z,且ω∈[0,3],所以ω=1.
由2kπ-≤2x+≤2kπ+(k∈Z),解得kπ-≤x≤kπ+(k∈Z),所以函数f(x)的增区间为[kπ-,kπ+](k∈Z).
(2)由(1)知f(x)=sin(2x+)++b.
因为x∈[0,],所以2x+∈[,].
当2x+∈[,],即x∈[0,]时,函数f(x)是增加的;当2x+∈[,],即x∈[,]时,函数f(x)是减少的.
又f(0)=f(),所以当f()>0≥f()或f()=0时,函数f(x)有且只有一个零点,即sin≤-b-0)的部分图象如图所示,其中M(m,0),N(n,2),P(π,0),且mn<0,则f(x)在下列区间中具有单调性的是( )
A. B.
C. D.
解析:选B.因为mn<0,所以m、n异号,根据题意可得m<0,n>0,又P(π,0),所以T>π且<π,即π0)的图象向左平移个单位得到函数g(x)的图象,若函数g(x)的图象关于直线x=ω对称且在区间内是增加的,则ω的值为( )
A. B.
C. D.
解析:选A.由题意得g(x)=sin=sin,因为函数g(x)的图象关于直线x=ω对称且在区间(-ω,ω)内是增加的,所以ω2+=+kπ,k∈Z,-+2mπ≤-ω2+,m∈Z,ω2+≤+2mπ,m∈Z,因此k≥0,kπ≤-2mπ,kπ≤2mπ,k,m∈Z,从而0≤-2mπ,0≤2mπ,m∈Z,即0≤m≤,m∈Z,所以m=0,k=0,ω=,选A.
3.如图,将绘有函数f(x)=sin(ωx+)(ω>0)部分图象的纸片沿x轴折成直二面角,若A,B之间的空间距离为,则f(-1)=________.
解析:由题设并结合图形可知,
AB==
==,得=4,则ω=,
所以f(-1)=sin(-+)=sin =.
答案:
4.若在区间(n,m)上,函数f(x)=2cos 2x的图象总在函数g(x)=-7-4sin x的图象的上方,则m-n的最大值为________.
解析:根据题意,函数f(x)=2cos 2x的图象总在函数g(x)=-7-4sin x的图象的上方可以转化为2cos 2x>-7-4sin x恒成立,即2cos 2x+7+4sin x>0.根据二倍角公式化简为4sin2x-4sin x-9<0⇒-0)的图象与x轴相邻两个交点的距离为.
(1)求函数f(x)的解析式;
(2)若将f(x)的图象向左平移m(m>0)个单位长度得到函数g(x)的图象恰好经过点(-,0),求当m取得最小值时,g(x)在[-,]上的增区间.
解: (1)函数f(x)的图象与x轴相邻两个交点的距离为,
得函数f(x)的最小正周期为T=2×=,得ω=1,
故函数f(x)的解析式为f(x)=sin(2x+).
(2)将f(x)的图象向左平移m(m>0)个单位长度得到函数g(x)=sin[2(x+m)+]=sin(2x+2m+)的图象,根据g(x)的图象恰好经过点(-,0),
可得sin(-+2m+)=0,即sin(2m-)=0,
所以2m-=kπ(k∈Z),m=+(k∈Z),
因为m>0,
所以当k=0时,m取得最小值,且最小值为.
此时,g(x)=sin(2x+).
因为x∈[-,],所以2x+∈[,].
当2x+∈[,],即x∈[-,-]时,g(x)是增加的,
当2x+∈[,],即x∈[,]时,g(x)是增加的.
综上,g(x)在区间[-,]上的增区间是
[-,-]和[,].