2020年高中数学第四章定积分的概念

2020年高中数学第四章定积分的概念

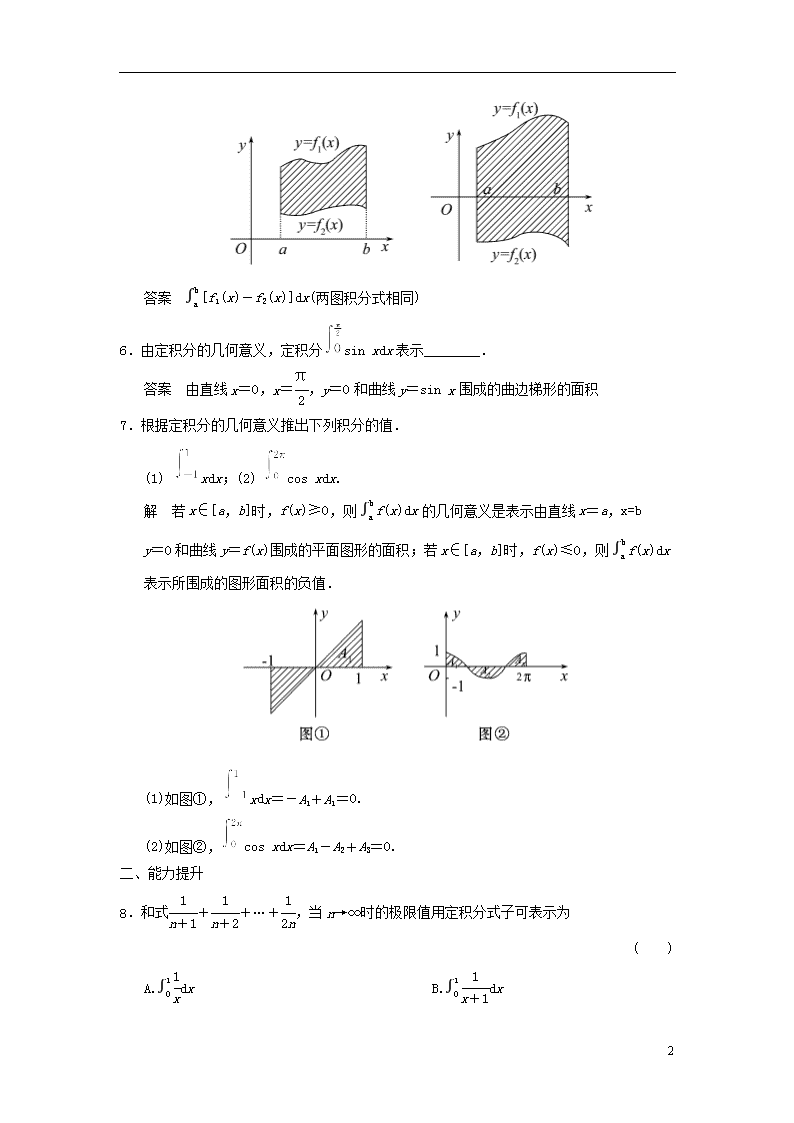
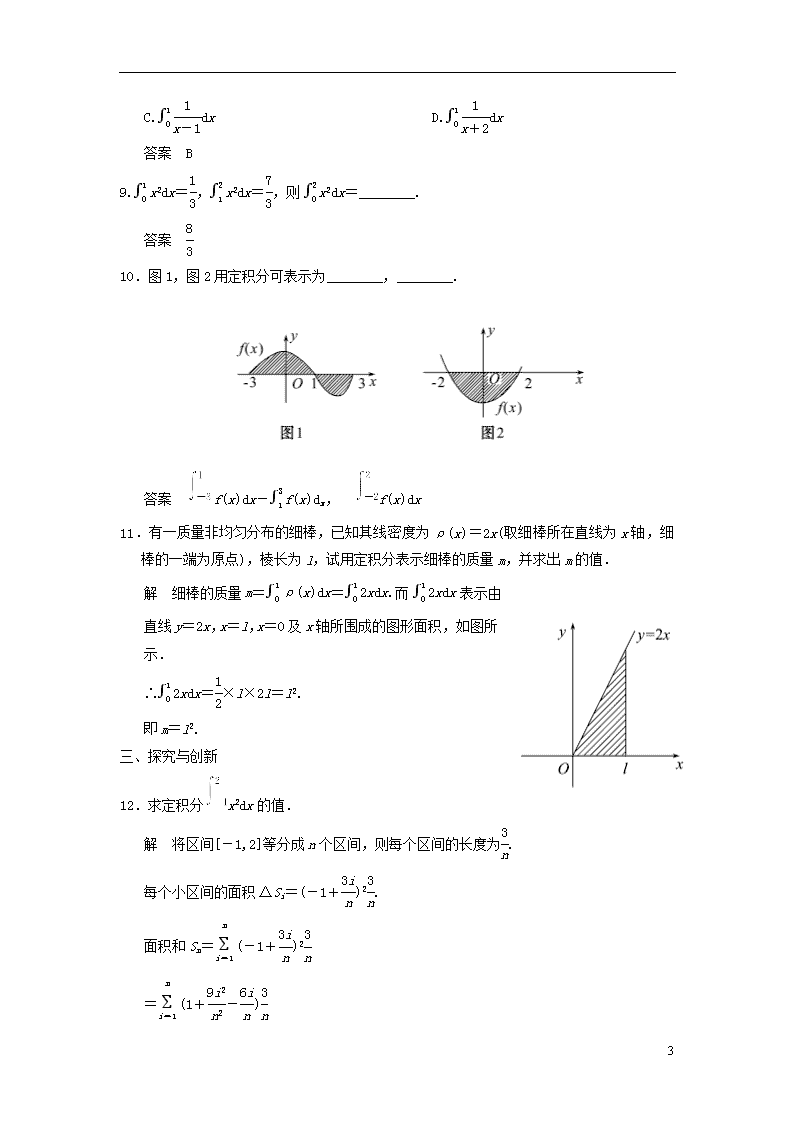
‎4．5.3　定积分的概念 一、基础达标 ‎1．下列命题不正确的是 ‎(　　)‎ A．若f(x)是连续的奇函数，则 ‎ B．若f(x)是连续的偶函数，则 C．若f(x)在[a，b]上连续且恒正，则f(x)dx>0‎ D．若f(x)在[a，b]上连续且f(x)dx>0，则f(x)在[a，b]上恒正 答案　D ‎2．直线x＝1，x＝－1，y＝0及曲线y＝x3＋sin x围成的平面图形的面积可表示为 ‎(　　)‎ A. B．2(x3＋sin x)dx C． D.(x3＋sin x)dx 答案　B ‎3．已知[f(x)＋g(x)]dx＝18，g(x)dx＝10，则f(x)dx等于 ‎(　　)‎ A．8 B．‎10 ‎‎ C．18 D．不确定 答案　A ‎4．已知定积分f(x)dx＝8，则f(x)为奇函数，则f(x)dx＝‎ ‎(　　)‎ A．0 B．‎16 ‎‎ C．12 D．8‎ 答案　A ‎5．根据定积分的几何意义，用积分表示如图所示各图的阴影部分的面积，‎ S＝________.‎ 4‎ 答案　[f1(x)－f2(x)]dx(两图积分式相同)‎ ‎6．由定积分的几何意义，定积分sin xdx表示________．‎ 答案　由直线x＝0，x＝，y＝0和曲线y＝sin x围成的曲边梯形的面积 ‎7．根据定积分的几何意义推出下列积分的值．‎ ‎(1) xdx；(2) cos xdx.‎ 解　若x∈[a，b]时，f(x)≥0，则f(x)dx的几何意义是表示由直线x＝a，x=b y＝0和曲线y＝f(x)围成的平面图形的面积；若x∈[a，b]时，f(x)≤0，则f(x)dx表示所围成的图形面积的负值．‎ ‎(1)如图①，xdx＝－A1＋A1＝0.‎ ‎(2)如图②，cos xdx＝A1－A2＋A3＝0.‎ 二、能力提升 ‎8．和式＋＋…＋，当n→∞时的极限值用定积分式子可表示为 ‎(　　)‎ A.dx B.dx C.dx D.dx 4‎ 答案　B ‎9.x2dx＝，x2dx＝，则x2dx＝________.‎ 答案　 ‎10．图1，图2用定积分可表示为________，________.‎ 答案　f(x)dx－f(x)dx，f(x)dx ‎11．有一质量非均匀分布的细棒，已知其线密度为ρ(x)＝2x(取细棒所在直线为x轴，细棒的一端为原点)，棱长为l，试用定积分表示细棒的质量m，并求出m的值．‎ 解　细棒的质量m＝ρ(x)dx＝2xdx.而2xdx表示由直线y＝2x，x＝l，x＝0及x轴所围成的图形面积，如图所示．‎ ‎∴2xdx＝×l×‎2l＝l2.‎ 即m＝l2.‎ 三、探究与创新 ‎12．求定积分x2dx的值．‎ 解　将区间[－1,2]等分成n个区间，则每个区间的长度为.‎ 每个小区间的面积ΔSi＝(－1＋)2.‎ 面积和Sn＝(－1＋)2 ‎＝(1＋－) ‎＝[n＋－×] ‎＝3＋(1＋)(2＋)－9(1＋)‎ 4‎ 当n→∞时，Sn→3＋×2－9＝3.‎ ‎∴x2dx＝3.‎ 4‎