2014浙江丽水中考数学(2)

2014浙江丽水中考数学(2)

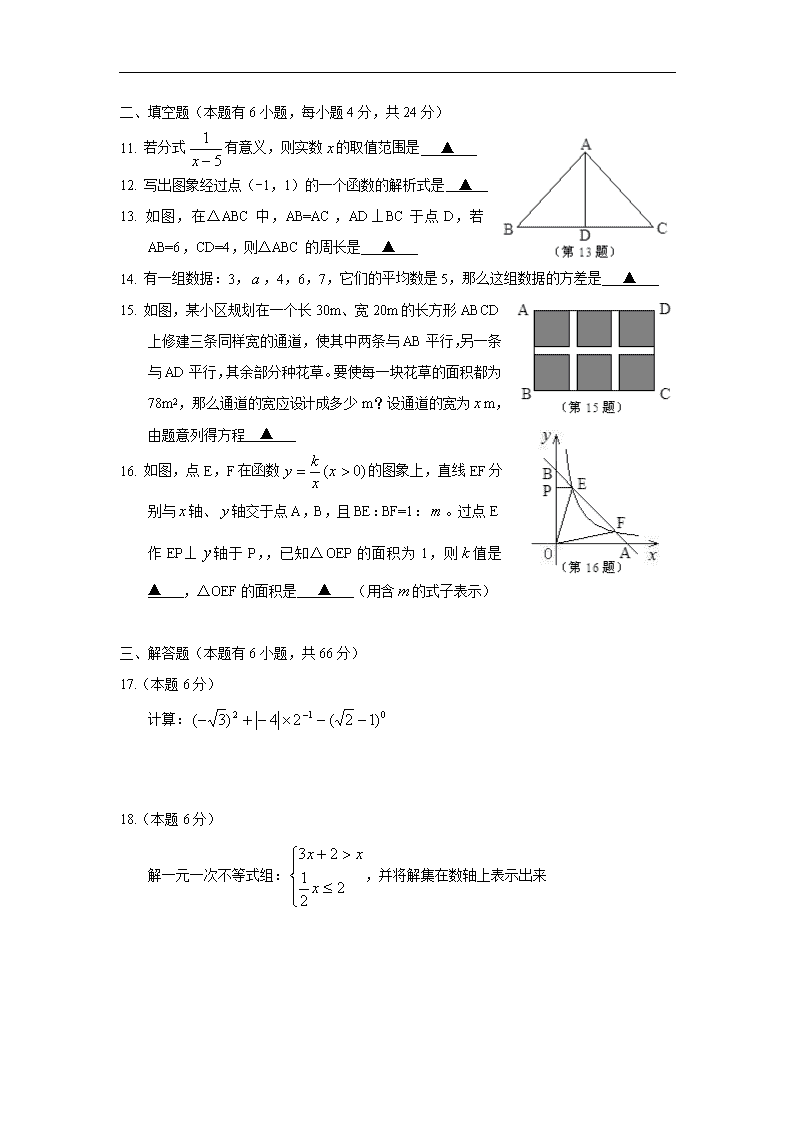
浙江省2014年初中毕业生学业考试（丽水卷）‎ 数 学 试 题 卷 满分为120分，考试时间为120分钟 参考公式：二次函数图象的顶点坐标是（，）；‎ 一组数据，，，…，的方差：‎ ‎（其中是这组数据的平均数）。‎ 一、选择题（本题有10小题，每小题3分，共30分）‎ ‎1. 在数，1，-3，0中，最大的数是 A. B. 1 C. -3 D. 0‎ ‎2. 下列四个几何体中，主视图为圆的是 ‎3. 下列式子运算正确的是 A. B. ‎ C. D. ‎ ‎4. 如图，直线∥，AC⊥AB，AC交直线于点C，∠1=60°，则∠2的度数是 A. 50° B. 45°‎ C. 35° D. 30°‎ ‎5. 如图，河坝横断面迎水坡AB的坡比是（坡比是坡面的铅直高度BC与水平宽度AC之比），坝高BC=3m，则坡面AB的长度是 A. 9m B. 6m C. m D. m ‎6. 某地区5月3日至5月9日这7天的日气温最高值统计图如图所示。从统计图看，该地区这7天日气温最高值的众数与中位数分别是 A. 23，25 B. 24，23‎ C. 23，23 D. 23，24‎ ‎7. 如图，小红在作线段AB的垂直平分线时，是这样操作的：分别以点A，B为圆心，大于线段AB长度一半的长为半径画弧，相交于点C，D，则直线CD即为所求。连结AC，BC，AD，BD，根据她的作图方法可知，四边形ADBC一定是 A. 矩形 B. 菱形 C. 正方形 D. 等腰梯形 ‎8. 在同一平面直角坐标系内，将函数的图象向右平移2个单位，再向下平移1个单位得到图象的顶点坐标是 A.（-3，-6） B. （1，-4） C. （1，-6） D. （-3，-4）‎ ‎9. 如图，半径为5的⊙A中，弦BC，ED所对的圆心角分别是∠BAC，∠EAD。已知DE=6，∠BSC+∠EAD=180°，则弦BC的弦心距等于 A. B. ‎ C. 4 D. 3‎ ‎10. 如图，AB=4，射线BM和AB互相垂直，点D是AB上的一个动点，点E在射线BM上，，作EF⊥DE并截取EF=DE，连结AF并延长交射线BM于点C。设，，则关于的函数解析式是 A. B. C. D. ‎ 二、填空题（本题有6小题，每小题4分，共24分）‎ ‎11. 若分式有意义，则实数的取值范围是 ▲ ‎ ‎12. 写出图象经过点（-1，1）的一个函数的解析式是 ▲ ‎ ‎13. 如图，在△ABC中，AB=AC，AD⊥BC于点D，若AB=6，CD=4，则△ABC的周长是 ▲ ‎ ‎14. 有一组数据：3，，4，6，7，它们的平均数是5，那么这组数据的方差是 ▲ ‎ ‎15. 如图，某小区规划在一个长30m、宽20m的长方形ABCD上修建三条同样宽的通道，使其中两条与AB平行，另一条与AD平行，其余部分种花草。要使每一块花草的面积都为78m2，那么通道的宽应设计成多少m？设通道的宽为m，由题意列得方程 ▲ ‎ ‎16. 如图，点E，F在函数的图象上，直线EF分别与轴、轴交于点A，B，且BE：BF=1：。过点E作EP⊥轴于P，，已知△OEP的面积为1，则值是 ▲ ，△OEF的面积是 ▲ （用含的式子表示）‎ 三、解答题（本题有6小题，共66分）‎ ‎17.（本题6分）‎ 计算：‎ ‎18.（本题6分）‎ 解一元一次不等式组：，并将解集在数轴上表示出来 ‎19.（本题6分）‎ 如图，正方形网格中的每个小的边长都是1，每个小正方形的顶点叫做格点。△ABC的三个顶点A，B，C都在格点上，将△ABC绕点A顺时针方向旋转90°得到△AB′C′‎ ‎（1）在正方形网格中，画出△AB′C′；‎ ‎（2）计算线段AB在变换到AB′的过程中扫过区域的面积 ‎20.（本题8分）‎ 学了统计知识后，小刚就本班同学上学“喜欢的出行方式”进行了一次调查。图（1）和图（2）是他根据采集的数据绘制的两幅不完整的统计图，请根据图中提供的信息解答以下问题：‎ ‎（1）补全条形统计图，并计算出“骑车”部分所对应的圆心角的度数；‎ ‎（2）如果全年级共600名同学，请估算全年级步行上学的学生人数；‎ ‎（3）若由3名“喜欢乘车”的学生，1名“喜欢步行”的学生，1名“喜欢骑车”的学生组队参加一项活动，欲从中选出2人担任组长（不分正副），列出所有可能的情况，并求出2人都是“喜欢乘车”的学生的概率。‎ ‎21.（本题8分）‎ 为了保护环境，某开发区综合治理指挥部决定购买A，B两种型号的污水处理设备共10台。已知用90万元购买A型号的污水处理设备的台数与用75万元购买B型号的污水处理设备的台数相同，每台设备价格及月处理污水量如下表所示：‎ 污水处理设备 A型 B型 价格（万元/台）‎ 月处理污水量（吨/台）‎ ‎220‎ ‎180‎ ‎（1）求的值；‎ ‎（2）由于受资金限制，指挥部用于购买污水处理设备的资金不超过165万元，问有多少种购买方案？并求出每月最多处理污水量的吨数 ‎22.（本题10分）‎ 如图，已知等边△ABC，AB=12，以AB为直径的半圆与BC边交于点D，过点D作DF⊥AC，垂足为F，过点F作FG⊥AB，垂足为G，连结GD。‎ ‎（1）求证：DF是⊙O的切线；‎ ‎（2）求FG的长；‎ ‎（3）求tan∠FGD的值。‎ ‎23.（本题10分）‎ 提出问题：‎ ‎（1）如图1，在正方形ABCD中，点E，H分别在BC，AB上，若AE⊥DH于点O，求证：AE=DH；‎ 类比探究：‎ ‎（2）如图2，在正方形ABCD中，点H，E，G，F分别在AB，BC，CD，DA上，若EF⊥HG于点O，探究线段EF与HG的数量关系，并说明理由；‎ 综合运用：‎ ‎（3）在（2）问条件下，HF∥GE，如图3所示，已知BE=EC=2，EO=2FO，求图中阴影部分的面积。‎ ‎24.（本题12分）‎ 如图，二次函数的图象经过点（1，4），对称轴是直线，线段AD平行于轴，交抛物线于点D。在轴上取一点C（0，2），直线AC交抛物线于点B，连结OA，OB，OD，BD。‎ ‎（1）求该二次函数的解析式；‎ ‎（2）求点B坐标和坐标平面内使△EOD∽△AOB的点E的坐标；‎ ‎（3）设点F是BD的中点，点P是线段DO上的动点，问PD为何值时，将△BPF沿边PF翻折，使△BPF与△DPF重叠部分的面积是△BDP的面积的？‎