专题四牛顿运动定律的应用(2)

专题四牛顿运动定律的应用(2)

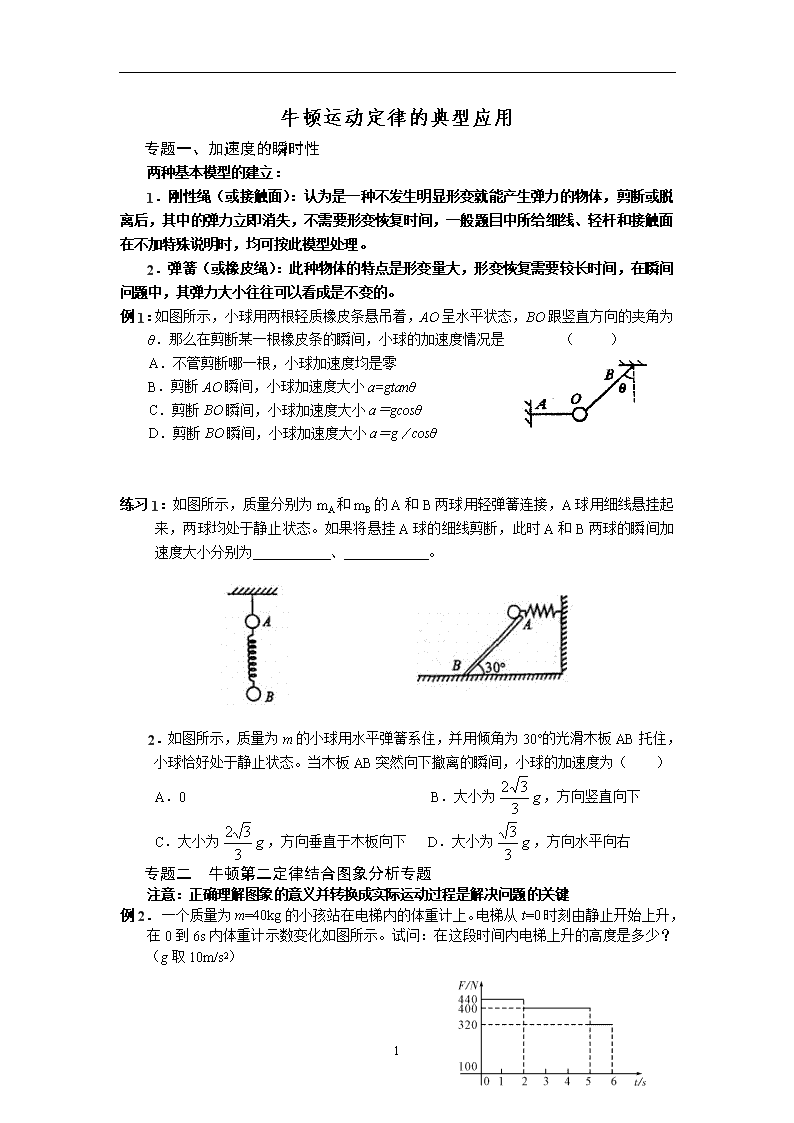
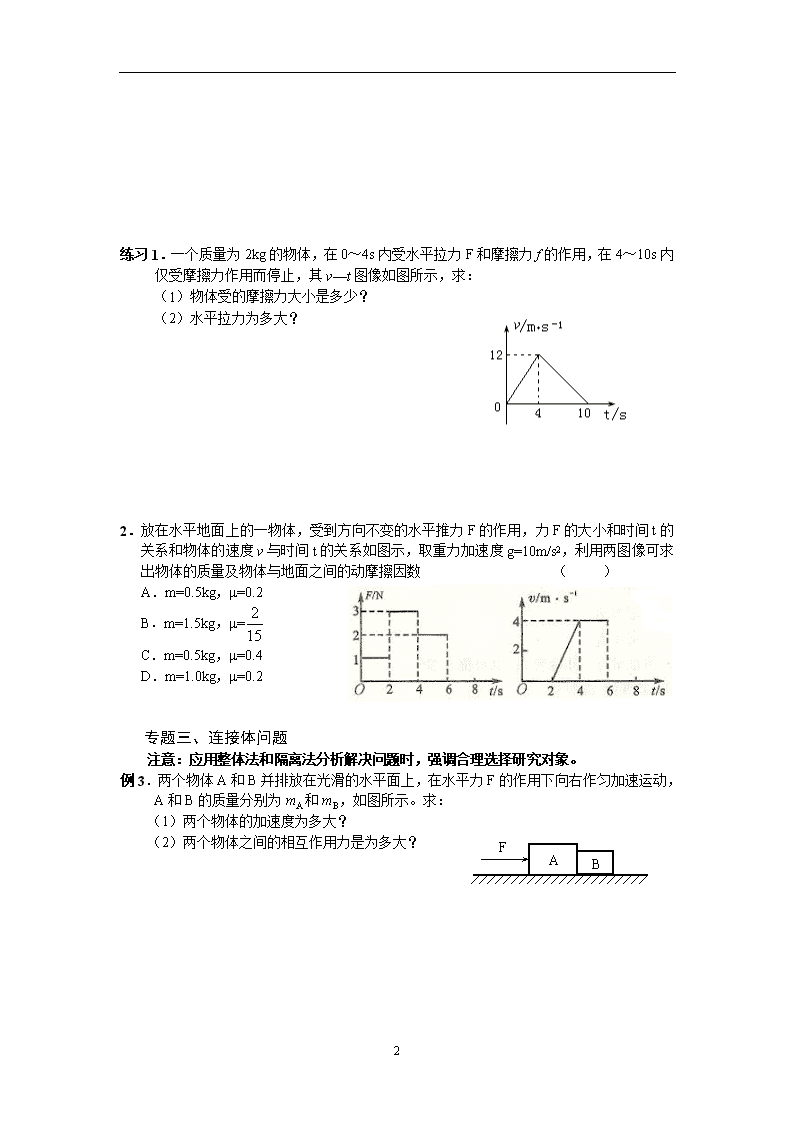
‎ ‎ 牛顿运动定律的典型应用 专题一、加速度的瞬时性 两种基本模型的建立：‎ ‎1．刚性绳（或接触面）：认为是一种不发生明显形变就能产生弹力的物体，剪断或脱离后，其中的弹力立即消失，不需要形变恢复时间，一般题目中所给细线、轻杆和接触面在不加特殊说明时，均可按此模型处理。‎ ‎2．弹簧（或橡皮绳）：此种物体的特点是形变量大，形变恢复需要较长时间，在瞬间问题中，其弹力大小往往可以看成是不变的。‎ 例1：如图所示，小球用两根轻质橡皮条悬吊着，AO呈水平状态，BO跟竖直方向的夹角为θ．那么在剪断某一根橡皮条的瞬间，小球的加速度情况是 （ ）‎ ‎ A．不管剪断哪一根，小球加速度均是零 ‎ B．剪断AO瞬间，小球加速度大小a=gtanθ ‎ C．剪断BO瞬间，小球加速度大小a＝gcosθ ‎ ‎ D．剪断BO瞬间，小球加速度大小a＝g／cosθ 练习1：如图所示，质量分别为mA和mB的A和B两球用轻弹簧连接，A球用细线悬挂起来，两球均处于静止状态。如果将悬挂A球的细线剪断，此时A和B两球的瞬间加速度大小分别为 、 。‎ ‎2．如图所示，质量为m的小球用水平弹簧系住，并用倾角为30°的光滑木板AB托住，小球恰好处于静止状态。当木板AB突然向下撤离的瞬间，小球的加速度为（ ）‎ ‎       A．0 B．大小为，方向竖直向下 ‎       C．大小为，方向垂直于木板向下 D．大小为，方向水平向右 专题二 牛顿第二定律结合图象分析专题 注意：正确理解图象的意义并转换成实际运动过程是解决问题的关键 例2． 一个质量为m=40kg的小孩站在电梯内的体重计上。电梯从t=0时刻由静止开始上升，在0到6s内体重计示数变化如图所示。试问：在这段时间内电梯上升的高度是多少？（g取10m/s2）‎ 4‎ ‎ ‎ 练习1．一个质量为2kg的物体，在0～4s内受水平拉力F和摩擦力f的作用，在4～10s内仅受摩擦力作用而停止，其v—t图像如图所示，求：‎ ‎（1）物体受的摩擦力大小是多少？‎ ‎（2）水平拉力为多大？‎ ‎2．放在水平地面上的一物体，受到方向不变的水平推力F的作用，力F的大小和时间t的关系和物体的速度v与时间t的关系如图示，取重力加速度g=10m/s2，利用两图像可求出物体的质量及物体与地面之间的动摩擦因数 （ ）‎ A．m=0.5kg，μ=0.2‎ B．m=1.5kg，μ=‎ C．m=0.5kg，μ=0.4 ‎ D．m=1.0kg，μ=0.2‎ 专题三、连接体问题 注意：应用整体法和隔离法分析解决问题时，强调合理选择研究对象。‎ 例3．两个物体A和B并排放在光滑的水平面上，在水平力F的作用下向右作匀加速运动，A和B的质量分别为mA和mB，如图所示。求：‎ ‎（1）两个物体的加速度为多大？‎ F A B ‎（2）两个物体之间的相互作用力是为多大？‎ 在上题中，若两个物体与地面间有摩擦，且A和B与地面之间的动摩擦因数均为μ，求：（1）两个物体的加速度？（2）两个物体间的相互作用力？‎ 4‎ ‎ ‎ 练习1．如图所示，在光滑的水平面上，两个物体A和B相对静止，质量分别为M和m，在水平力F的作用下，一起向右做匀加速直线运动，求：‎ ‎（1）两个物体的加速度是多大？‎ ‎（2）两个物体之间的静摩擦力是多大？‎ ‎（3）若要保证A与B不发生相对滑动，F的取值范围是什么？‎ F A B 专题四 ‎ 临界问题分析专题 注意：1、在题目当中找到关键的词语：如物体恰好、刚好达到某种状态；‎ ‎ 2、利用题目条件分析哪个力会达到零或某种平衡的临界状态。‎ 例4．如图所示，质量m=0.2kg的小球挂在倾角θ=53°的光滑斜面的固定铁杆上，当斜面和小球以a1=5m/s2的加速度向右匀加速运动时，小球对绳的拉力和对斜面的压力分别为多大？当斜面和小球都以a2=8 m/s2的加速度向右匀加速运动时，小球对绳的拉力和对斜面的压力又分别为多大？（g取10 m/s2）‎ ‎ ‎ 4‎ ‎ ‎ 练习1．如图所示，在劲度系数为k的弹簧下端挂有质量为m的物体，开始用托盘托住物体，使弹簧保持原长，然后托盘以加速度a匀加速下降（a＜g），求经过多长时间托盘与物体分离。‎ 4‎