- 2021-04-16 发布 |
- 37.5 KB |
- 11页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2012年福州中考数学试卷
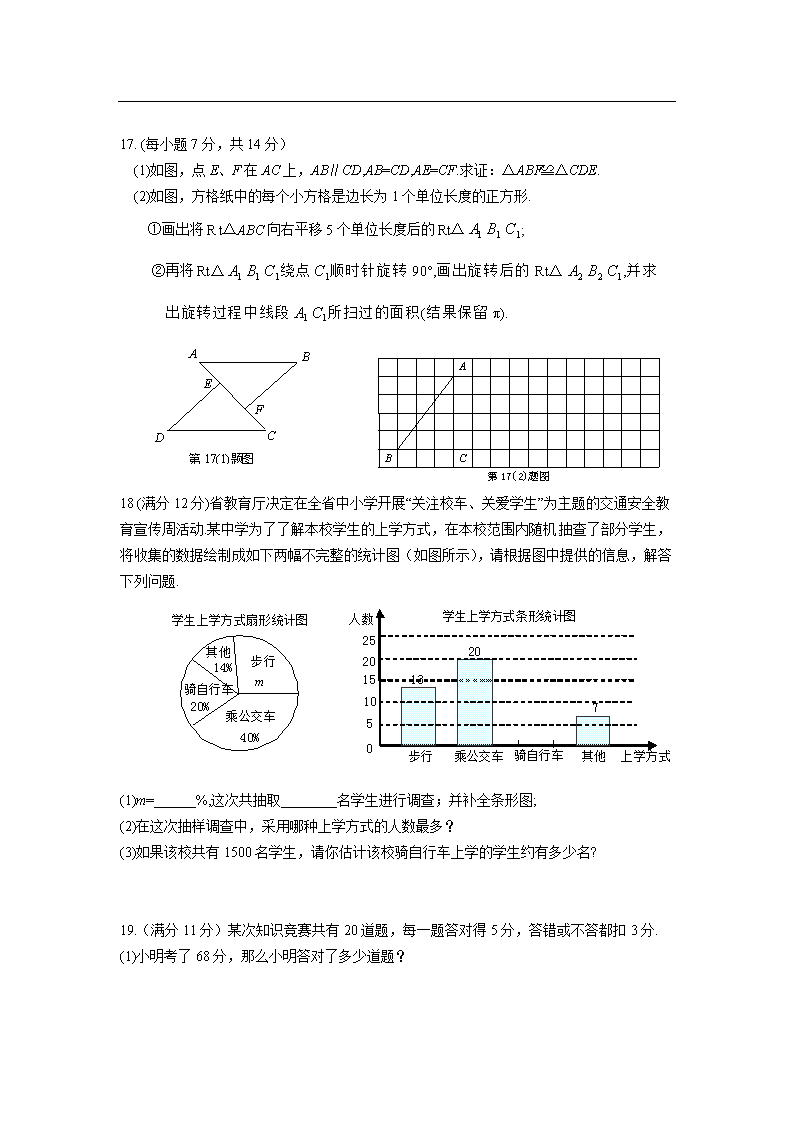
2012年福州市初中毕业会考、高级中等学校招生考试 数 学 试 卷 (本卷共四页,三大题,共22小题;满分150分,考试时间120分钟) 友情提示:所有答案都必须填涂在答题卡的相应的位置上,答在本试卷一律无效. 毕业学校_________________姓名___________考生号_________[来源:www.shulihua.netwww.shulihua.net] 一、选择题(共10小题,每题4分,满分40分;每小题只有一个正确的选项,请在答题卡的相应位置填涂) 1. 3的相反数是 A.-3 B. C.3 D. 2.今年参观“5·18”海交会的总人数约为498000人,将498000用科学记数法表示为 A. B. C. D. 3. 如图是由4个大小相同的正方体组合而成的几何题,其主视图是 4. 如图,直线a∥b,∠1=70º,那么∠2的度数是 A.50º B.60º C.70º D.80º (注:本题似乎应加上条件:直线a、b被直线c所截) 5. 下列计算正确的是 A.a+a=2a B. C. D. 6. 式子在实数范围内有意义,则x的取值范围是 A.x<1 B,x≤1 C.x>1 D x≥1 7. 某射击运动员在一次射击练习中,成绩(单位:环)记录如下:8,9,8,7,10.这组数据的平均数和中位数分别是[来源:www.shulihua.netwww.shulihua.net] A.8,8 B.8.4,8 C.8.4,8.4 D.8,8.4 8. ⊙和的半径分别是3cm和4cm,如果=7cm,则这两圆的位置关系是 A.内含 B.相交 C.外切 D.外离 9.如图,从热气球C处测得地面A、B两点的俯角分别为30º、45º,如果此时热气球C处的高度CD为100米,点A、D、B在同一条直线上,则A、B两点的距离是 A.200米 B.米 C.米 D.米 10. 如图,过点C(1,2)分别作x轴、y轴的平行线,交直线y=-x+6于A、B两点,若反比例函数(x>0)的图象与△ABC有公共点,则k的取值范围是 A.2≤k≤9 B.2≤k≤8 C.2≤k≤5 D.5≤k≤8 二、填空题(共5小题,每题4分,满分20分;请将正确答案填在答题卡相应位置) 11.分解因式:=___________. 12. 一个袋子中装有3个红球和2个绿球,这些球除了颜色外都相同,从袋子中随机摸出一个球,则摸到红球的概率是___________. 13. 若是整数,则正整数n的最小值是_______. 14. 计算:=___________. 15. 如图,已知△ABC,AB=AC=1,∠A=36º,∠ABC的平分线BD交AC于点D,则AD的长是___________,cosA的值是_________(结果保留根号). 三、解答题(满分90分;请将正确答案及解答过程填在答题卡相应位置.作图或添辅助线用铅笔画完,再用黑色签字笔描黑) 16.(每小题7分,共14分) (1)计算:|-3|+(π+1)-. (2). 17. (每小题7分,共14分) (1)如图,点E、F在AC上,AB∥CD,AB=CD,AE=CF.求证:△ABF≌△CDE. (2)如图,方格纸中的每个小方格是边长为1个单位长度的正方形. ①画出将Rt△ABC向右平移5个单位长度后的Rt△; ②再将Rt△绕点顺时针旋转90º,画出旋转后的Rt△,并求出旋转过程中线段所扫过的面积(结果保留π). 18 (满分12分)省教育厅决定在全省中小学开展“关注校车、关爱学生”为主题的交通安全教育宣传周活动.某中学为了了解本校学生的上学方式,在本校范围内随机抽查了部分学生,将收集的数据绘制成如下两幅不完整的统计图(如图所示),请根据图中提供的信息,解答下列问题. (1)m=______%,这次共抽取________名学生进行调查;并补全条形图; (2)在这次抽样调查中,采用哪种上学方式的人数最多? (3)如果该校共有1500名学生,请你估计该校骑自行车上学的学生约有多少名? 19.(满分11分)某次知识竞赛共有20道题,每一题答对得5分,答错或不答都扣3分. (1)小明考了68分,那么小明答对了多少道题? (2)小亮获得二等奖(70~90分),请你算算小亮答对了几道题? 20.(满分12分)如图,AB为⊙O的直径,C为⊙O上一点,AD和过C点的切线互相垂直,垂足为D.AD交⊙O于点E. (1)AC平分∠DAB;[来源:www.shulihua.net] (2)若∠B=60º,CD=,求AE的长. [来源:www.shulihua.net] 21.(满分13分)如图①,在Rt△ABC中,∠C=90º,AC=6,BC=8,动点P从点A开始沿边AC向点C以每秒1个单位长度的速度运动,动点Q从点C开始沿边CB向点B以每秒2个单位长度的速度运动,过点P作PD∥BC,交AB于点D,连接PQ.点P、Q分别从点A、C同时出发,当其中一点到达端点时,另一点也随之停止运动,设运动时间为t秒(t≥0). (1)直接用含t的代数式分别表示:QB=__________,PD=___________. (2)是否存在t的值,使四边形PDBQ为菱形?若存在,求出t的值;若不存在,说明理由.并探究如何改变点Q的速度(匀速运动),使四边形PDBQ在某一时刻为菱形,求点Q的速度; (3)如图②,在整个运动过程中,求出线段PQ中点M所经过的路径长. 22.(满分14分)如图①,已知抛物线(a≠0)经过A(3,0)、B(4,4)两点. (1)求抛物线的解析式; (2)将直线OB向下平移m个单位长度后,得到的直线与抛物线只有一个公共点D,求m的值及点D的坐标; (3)如图②,若点N在抛物线上,且∠NBO=∠ABO,则在(2)的条件下,求出所有满足△POD∽△NOB的点P的坐标(点P、O、D分别与点N、O、B对应). [来源:www.shulihua.net]查看更多