七年级下数学课件《平行线的性质》课件1_冀教版

七年级下数学课件《平行线的性质》课件1_冀教版

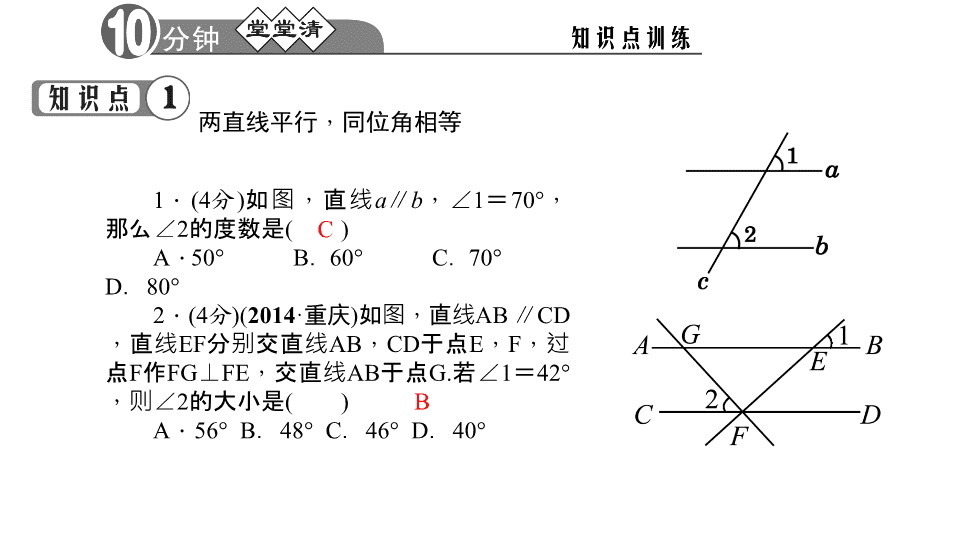
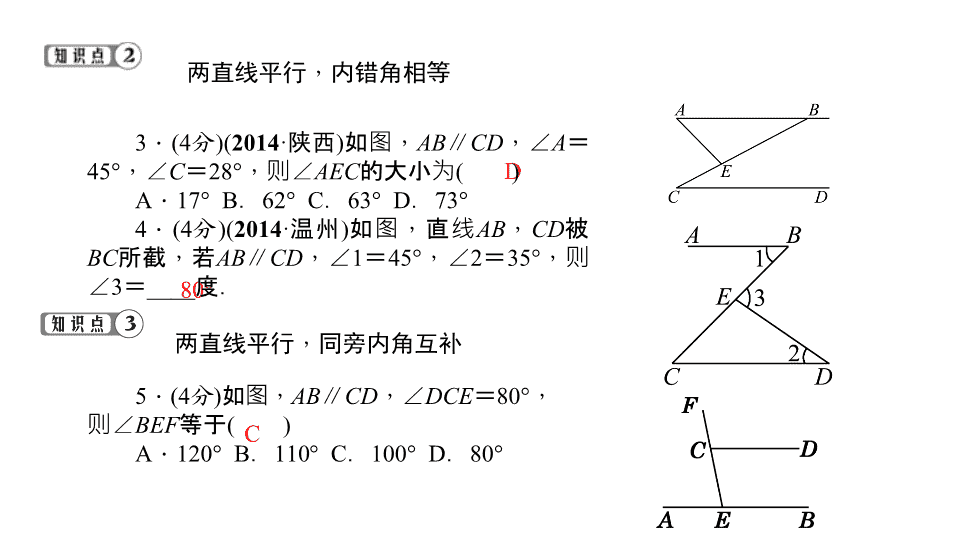
7.5　平行线的性质 第1课时　平行线的性质 得分________　卷后分________　评价________ 相等 相等 平行线的性质定理： 1．两条平行线被第三条直线所截，同位角相 等．简称：两直线平行，同位角____． 2．两条平行线被第三条直线所截，内错角相等， 同旁内角互补．简称：两直线平行，内错角____； 两直线平行，同旁内角____．互补 C B 两直线平行，同位角相等 1．(4分)如图，直线a∥b，∠1＝70°， 那么∠2的度数是(　　) A ． 5 0 ° 　 　 　 　 B ． 6 0 °　　　　 C．70°　　　　D．80° 2．(4分)(2014·重庆)如图，直线AB ∥CD，直线EF分别交直线AB，CD于点E， F，过点F作FG⊥FE，交直线AB于点G.若 ∠1＝42°，则∠2的大小是(　　) A．56° B．48° C．46° D．40° D 80° C 两直线平行，内错角相等 3．(4分)(2014·陕西)如图，AB∥CD，∠A＝ 45°，∠C＝28°，则∠AEC的大小为(　　) A．17° B．62° C．63° D．73° 4．(4分)(2014·温州)如图，直线AB，CD被 BC所截，若AB∥CD，∠1＝45°，∠2＝35°， 则∠3＝____度． 两直线平行，同旁内角互补 5．(4分)如图，AB∥CD，∠DCE＝80°， 则∠BEF等于(　　) A ． 1 2 0 ° B ． 11 0 ° C ． 1 0 0 ° D．80° 6．(4分)如图，AB∥CD，直线EF 交AB于点E，交CD于点F，EG平分 ∠BEF，交CD于点G，∠1＝50°，则 ∠2等于(　　) A ． 5 0 ° B ． 6 0 ° C ． 6 5 ° D．90° 7．(4分)如图所示，直线l1∥l2， AB⊥CD，∠1＝34°，那么∠2的度数 是____． 8．(4分)如图，AD∥EG∥BC， AC∥EF，则图中与∠1相等的角(不含 ∠1)有____个，若∠1＝50°，则 ∠AHG＝____． C 56° 5 130° 10．(4分)已知：如图，如果∠1＝∠2， DC∥FE，DE∥AC，那么FE是∠BED的平分 线的证明过程如下，请你填空： 证明：∵AC∥DE(　　)， ∴∠2＝____( )． 又∵DC∥EF(　　)， ∴∠1＝∠3(　　 )． ∠4＝∠CDE(两直线平行，内错角相 等)． 又∵∠1＝∠2(　)， ∴∠3＝∠4(　 　)， ∴FE平分∠BED( 　　)． 已知 已知 ∠CDE 两直线平行，内错角相等 两直线平行，同位角相等 　已知 等量代换 角平分线定义 D A C 一、选择题(每小题4分，共16分) 11．如图，AB∥CD，∠C＝80°， ∠CAD＝60°，则∠BAD的度数等于(　 　) A．60°　　　　　B．50° C．45° D．40° 12．(2014·德州)如图，AD是∠EAC的平 分线，AD∥BC，∠B＝30°，则∠C为(　 　) A．30° B．60° C．80° D．120° 13．如图，AB∥EF∥DC，AD∥BC， AC是∠BAD的平分线，则与∠6相等的角有 (　 ) A．3个 B．4个 C．5个 D．6个 14．如图，小明在操场上从A点出发， 先沿南偏东30°方向走到B点，再沿南偏东 60°方向走到C点．这时，∠ABC的度数是(　 　) A．120° B．135° C．150° D．160° 二、填空题(每小题4分，共12分) 15．如图，AB∥CD，∠B＝42°，∠2 ＝35°，则∠1＝____，∠A＝____，∠ACB ＝____，∠BCD＝____. 16．如图，已知∠1＝∠2，∠D＝78°， 则∠BCD＝____. C 42° 35° 103° 138° 102° 17．如图所示，直线a与直线b互相平行，则 |x－y|的值是____． 三、解答题(共32分) 18．(10分)如图，若AB∥CD，且∠1＝∠2， 试判断AM与CN的位置关系，并说明理由． 解：AM∥CN.理由：∵AB∥CD， ∴ ∠ B A E ＝ ∠ A C D . 又 ∵ ∠ 1 ＝ ∠ 2 ， ∴∠MAE＝∠NCA，∴AM∥CN 20 19．(10分)如图，AD∥BE，∠1＝∠2， 那么∠A＝∠E吗？请说明理由． 解：∠A＝∠E.理由：∵∠1＝∠2(已知)， ∴AC∥DE(内错角相等，两直线平行)， ∴∠3＝∠E(两直线平行，内错角相等)， ∵AD∥BE(已知)，∴∠3＝∠A(两直线平行， 同位角相等)，∴∠A＝∠E(等量代换) 【综合运用】 20．(12分)如图，∠ADC＝∠ABC，∠1 ＋∠2＝180°，DA是∠FDB的平分线，试说 明BC是∠DBE的平分线． 解：∵∠2＝∠5＋∠6，∠1＋∠3＋∠4 ＝180°，∠1＋∠2＝180°，∴∠5＋∠6＝ ∠3＋∠4.∵∠ADC＝∠ABC，∠3＋∠ABC ＝180°，∠6＋∠ADC＝180°，∴∠3＝ ∠6，∴∠4＝∠5.又∵DA平分∠FDB， ∴∠3＝∠6＝∠5＝∠4，∴BC是∠DBE的平 分线．