- 2021-04-16 发布 |
- 37.5 KB |
- 4页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
中考数学填空题专项训练
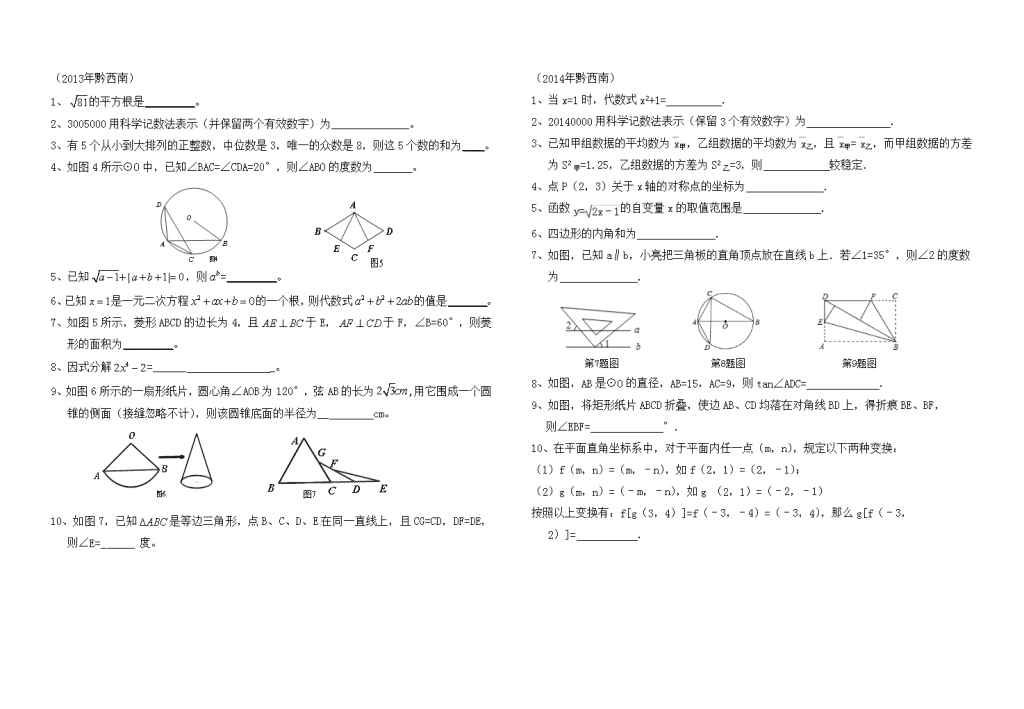
中考数学 填空题专项训练 (2011年黔西南) 1、因式分解:x3-9x= . 2、小程对本班50名同学进行了“我最喜爱的运动项目”的调查,统计出了最喜爱跳绳、羽毛球、篮球、乒乓球、踢毽子等运动项目的人数.根据调查结果绘制了人数分布直方图.若将其转化为扇形统计图,那么最喜爱打篮球的人数所在扇形区域的圆心角的度数为 . 第2题图 第4题图 3、已知圆锥的母线长为30,侧面展开后所得扇形的圆心角为120°,则该圆锥的底面半径为 . 4、如图,点E(0,4),O(0,0),C(5,0)在⊙A上,BE是⊙A上的一条弦,则tan∠OBE= . 5、某市今年起调整居民用水价格,每立方米水费上涨20%,小方家去年12月份的水费是26元,而今年5月份的水费是50元.已知小方家今年5月份的用水量比去年12月份多8立方米,设去年居民用水价格为x元/立方米,则所列方程为 . 6、如图,在Rt△ABC中,∠C=90°,BC=6cm,AC=8cm,按图中所示方法将△BCD沿BD折叠,使点C落在AB边的C′点,那么△ADC′的面积是 . 第6题图 第7题图 第8题图 7、已知:如图,O为坐标原点,四边形OABC为矩形,A(10,0),C(0,4),点D是OA的中点,点P在BC上运动,当△ODP是腰长为5的等腰三角形时,则P点的坐标为 . 8、如图,在Rt△ABC中,∠C=90°,CA=CB=4,分别以A、B、C为圆心,以AC为半径画弧,三条弧与边AB所围成的阴影部分的面积是 . (2012年黔西南) 1、在2011年,贵州省“旅发大会”在我州召开,据统计,“万峰林”风景区招待游客的人数一年大约为30.1万人,这一数据用科学计数法表示为 。 2、已知一个样本-1,0,2,x,3,它们的平均数是2,则这个样本的方差S2= 。 3、计算: 。 4、已知反比例函数的图象经过点(m,2)和(-2,3),则m的值为 。 5、已知圆锥的底面半径为10cm,它的展开图的扇形的半径为30cm,则这个扇形圆心角的度数是 。 6、已知和是同类项,则 。 7、如图,在梯形ABCD中,AD//BC,对角线AC、BD相交于点O,若AD=1,BC=3,△AOD的面积为3,则△BOC的面积为 。 第7题图 第8题图 第10题图 8、如图,在△ABC中,∠ACB=90°,D是BC的中点,DE⊥BC,CE//AD,若AC=2,CE=4,则四边形ACEB的周长为 。 9、分解因式: 。 10、把一张矩形纸片(矩形ABCD)按如图方式折叠,使顶点B和点D重合,折痕为EF,若AB=3cm,BC=5cm,则重叠部分△DEF的面积为 cm 2。 (2013年黔西南) 1、的平方根是_________。 2、3005000用科学记数法表示(并保留两个有效数字)为______________。 3、有5个从小到大排列的正整数,中位数是3,唯一的众数是8,则这5个数的和为____。 4、如图4所示⊙O中,已知∠BAC=∠CDA=20°,则∠ABO的度数为 。[来 源:学科+网] 5、已知,则=_________。 6、已知是一元二次方程的一个根,则代数式的值是_______。 7、如图5所示,菱形ABCD的边长为4,且于E,于F,∠B=60°,则菱形的面积为_________。 8、因式分解=______ _。 9、如图6所示的一扇形纸片,圆心角∠AOB为120°,弦AB的长为,用它围成一个圆锥的侧面(接缝忽略不计),则该圆锥底面的半径为__ cm。 10、如图7,已知是等边三角形,点B、C、D、E在同一直线上,且CG=CD,DF=DE,则∠E=_ 度。 (2014年黔西南) 1、当x=1时,代数式x2+1= . 2、20140000用科学记数法表示(保留3个有效数字)为 . 3、已知甲组数据的平均数为甲,乙组数据的平均数为乙,且甲=乙,而甲组数据的方差为S2甲=1.25,乙组数据的方差为S2乙=3,则 较稳定. 4、点P(2,3)关于x轴的对称点的坐标为 . 5、函数的自变量x的取值范围是 . 6、四边形的内角和为 . 7、如图,已知a∥b,小亮把三角板的直角顶点放在直线b上.若∠1=35°,则∠2的度数为 . 第7题图 第8题图 第9题图 8、如图,AB是⊙O的直径,AB=15,AC=9,则tan∠ADC= . 9、如图,将矩形纸片ABCD折叠,使边AB、CD均落在对角线BD上,得折痕BE、BF, 则∠EBF= °. 10、在平面直角坐标系中,对于平面内任一点(m,n),规定以下两种变换: (1)f(m,n)=(m,﹣n),如f(2,1)=(2,﹣1); (2)g(m,n)=(﹣m,﹣n),如g (2,1)=(﹣2,﹣1) 按照以上变换有:f[g(3,4)]=f(﹣3,﹣4)=(﹣3,4),那么g[f(﹣3,2)]= . 参考答案 (2011年黔西南) 1、x ( x-3 )( x+3 ) 2、144° 3、10 4、 5、 6、6cm2 7、P(3,4)或(2,4)或(8,4) 8、 (2012年黔西南) 1、3.01×105 2、6 3、-1.14 4、-3 5、120° 6、1 7、27 8、10+ 9、 10、 (2013年黔西南) 1、 2、 3、22 4、 5、1 6、1 7、 8、 9、 10、15 (2014年黔西南) 1、2 2、2.01×107 3、甲 4、(2,﹣3) 5、x≥ 6、360° 7、55° 8、 9、45° 10、(3,2)查看更多