- 2021-04-16 发布 |
- 37.5 KB |
- 7页

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2018圆中考大题
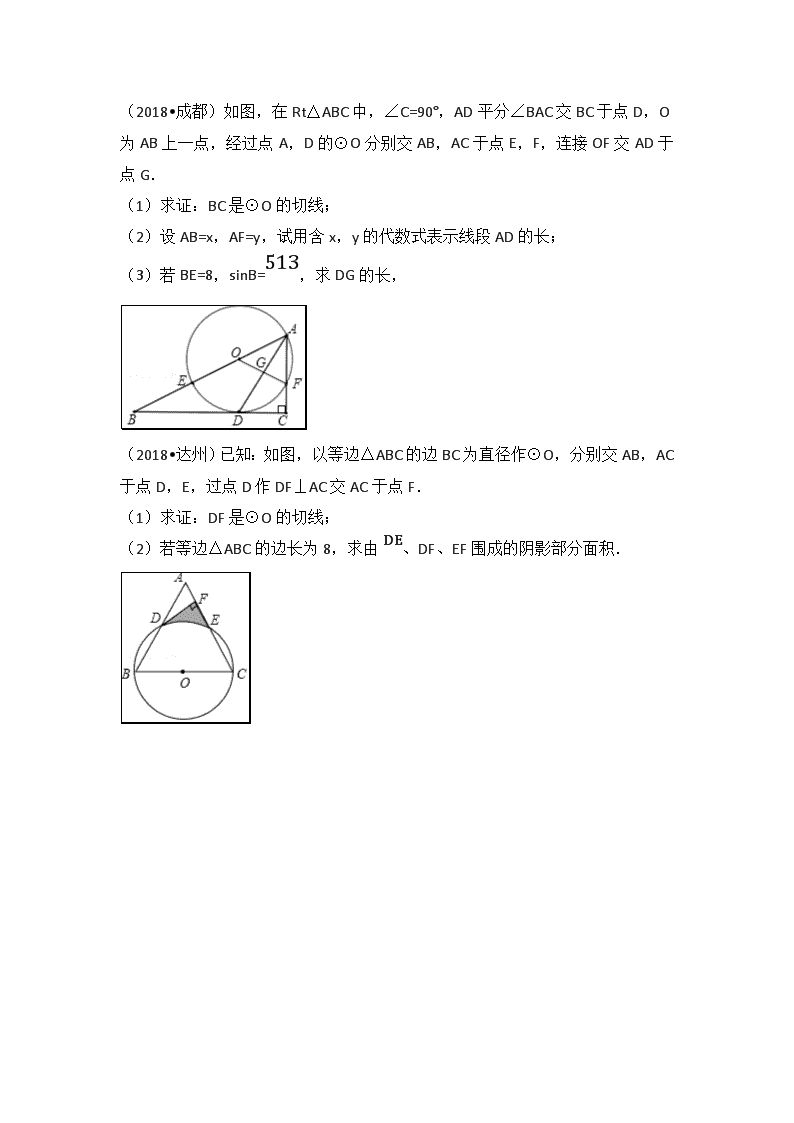
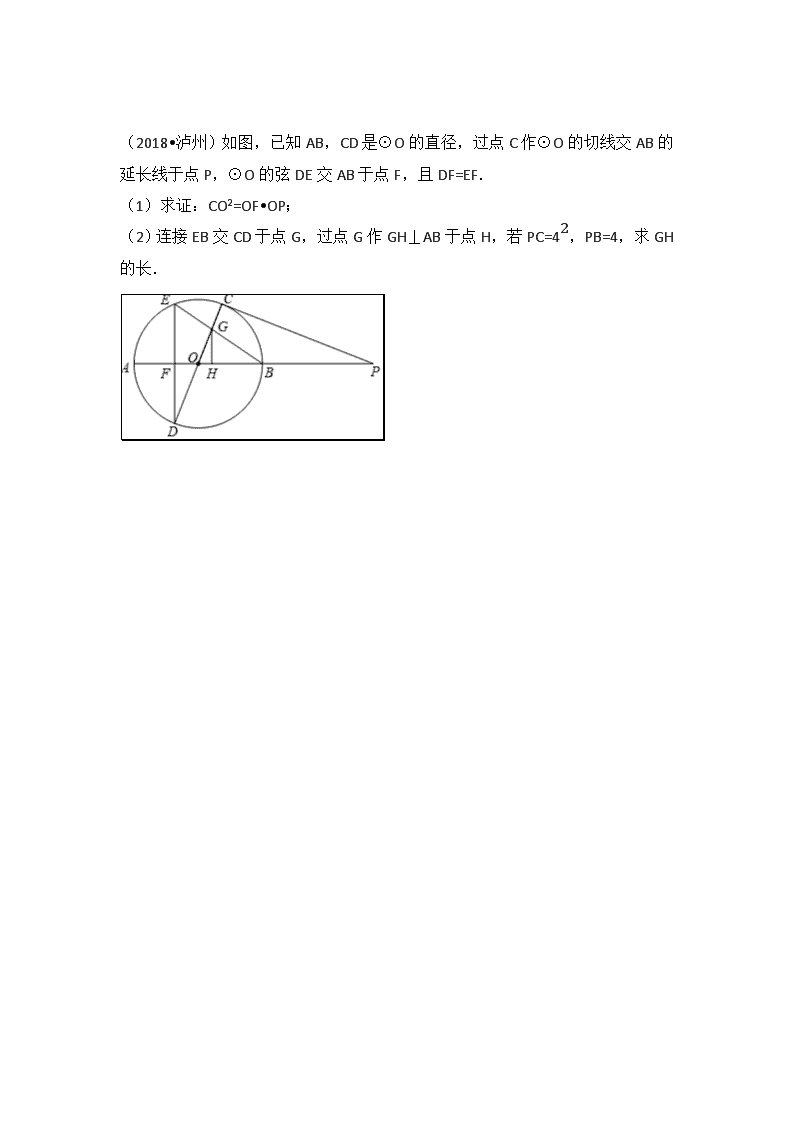
(2018•成都)如图,在Rt△ABC中,∠C=90°,AD平分∠BAC交BC于点D,O为AB上一点,经过点A,D的⊙O分别交AB,AC于点E,F,连接OF交AD于点G. (1)求证:BC是⊙O的切线; (2)设AB=x,AF=y,试用含x,y的代数式表示线段AD的长; (3)若BE=8,sinB=513,求DG的长, (2018•达州)已知:如图,以等边△ABC的边BC为直径作⊙O,分别交AB,AC于点D,E,过点D作DF⊥AC交AC于点F. (1)求证:DF是⊙O的切线; (2)若等边△ABC的边长为8,求由DE、DF、EF围成的阴影部分面积. (2018•泸州)如图,已知AB,CD是⊙O的直径,过点C作⊙O的切线交AB的延长线于点P,⊙O的弦DE交AB于点F,且DF=EF. (1)求证:CO2=OF•OP; (2)连接EB交CD于点G,过点G作GH⊥AB于点H,若PC=42,PB=4,求GH的长. (2018•达州)阅读下列材料: 已知:如图1,等边△A1A2A3内接于⊙O,点P是A1A2上的任意一点,连接PA1,PA2,PA3,可证:PA1+PA2=PA3,从而得到:PA1+PA2PA1+PA2+PA3=12是定值. (1)以下是小红的一种证明方法,请在方框内将证明过程补充完整; 证明:如图1,作∠PA1M=60°,A1M交A2P的延长线于点M. ∵△A1A2A3是等边三角形, ∴∠A3A1A2=60°, ∴∠A3A1P=∠A2A1M 又A3A1=A2A1,∠A1A3P=∠A1A2P, ∴△A1A3P≌△A1A2M ∴PA3=MA2=PA2+PM=PA2+PA1. ∴PA1+PA2PA1+PA2+PA3=12,是定值. (2)延伸:如图2,把(1)中条件“等边△A1A2A3”改为“正方形A1A2A3A4 ”,其余条件不变,请问:PA1+PA2PA1+PA2+PA3+PA4还是定值吗?为什么? (3)拓展:如图3,把(1)中条件“等边△A1A2A3”改为“正五边形A1A2A3A4A5”,其余条件不变,则PA1+PA2PA1+PA2+PA3+PA4+PA5= (5-1)28 (只写出结果).查看更多