2014四川省内江市中考数学

2014四川省内江市中考数学

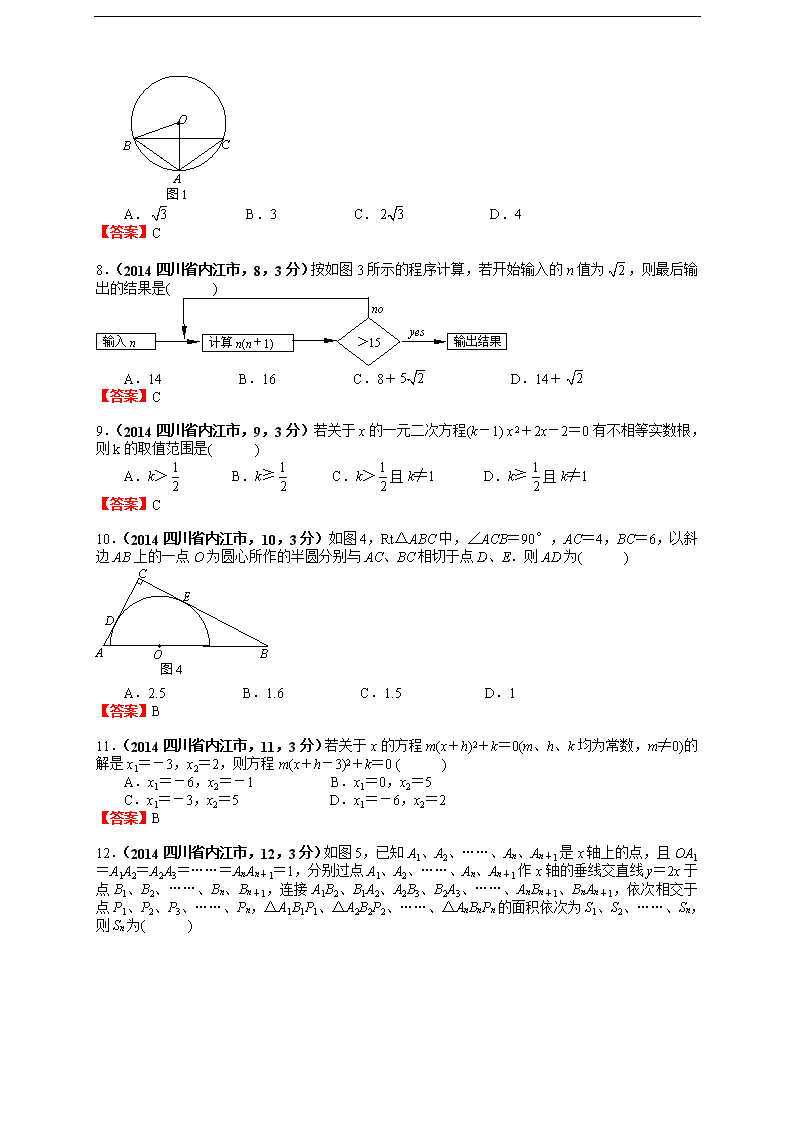
内江市2014年初中学业水平考试及高中阶段学校招生考试 数 学 本本试卷为A卷和B卷两部分，A卷1至4页，滿分100分；B卷5至6页，满分60分。全卷满分160分，考试时间120分钟。‎ 注意亊项：‎ ‎1．答题前请仔细阅读答题卡上的注意事项。‎ ‎2．所有试题的答案必须按号填写在答题卡相应的位置上，在试卷上、草稿纸上答题无效。‎ ‎3．考试结束后，监考人员将试卷和答题卡一并收回。‎ A卷（共100分）‎ 一、选择题(本大题共12小題，每小题3分，共36分．在毎小题给出的四个选项中只有一项是符合题目要求的．)‎ ‎1．（2014四川省内江市，1，3分）的相反数是( )‎ A．－ B． C．－ D．‎ ‎【答案】A ‎2．（2014四川省内江市，2，3分）一种微粒的半径是0.000 ‎04米，这个数据用科学记数法表示为( )‎ A．4×l06 B．4×l0－‎6 C．4×l0－5 D．4×l05 ‎ ‎【答案】C ‎3．（2014四川省内江市，3，3分）下列调查中，①调査本班同学的视力；②调查一批节能灯管的使用寿命；③为保证“神舟9号”的成功发射，对其零部件进行检查；④对乘坐某班次客车的乘客进行安检．其中适合采用抽样调查的是( )‎ A．① B．② C．③ D．④‎ ‎【答案】B ‎4．（2014四川省内江市，4，3分）如图1，桌面上有一个一次性纸杯，它的正视图应是( )‎ 图‎1 A． B． C． D．‎ ‎【答案】D ‎5．（2014四川省内江市，5，3分）在函数中，自变量x的取值范围是( )‎ A．x≥－2且x≠1 B．x≤2且x≠‎1 C．x≠1 D．x≤－2‎ ‎【答案】A ‎6．（2014四川省内江市，6，3分）某班数学兴趣小组10名同学的年龄情况如下表：‎ 年龄（岁）‎ ‎12‎ ‎13‎ ‎14‎ ‎15‎ 人数 ‎1‎ ‎4‎ ‎4‎ ‎1‎ 则这10名同学年龄的平均数和中位数分别是( )‎ A．13.5，13.5 B．13.5，‎13 ‎‎ C．13，13.5 D．13，14‎ ‎【答案】A ‎7．（2014四川省内江市，7，3分）如图2，⊙O是△ABC的外接圆，∠AOB＝60°，AB＝AC＝2，则弦BC的长为( )‎ O C A B 图1‎ A． B．‎3 C． D．4‎ ‎【答案】C ‎8．（2014四川省内江市，8，3分）按如图3所示的程序计算，若开始输入的n值为，则最后输出的结果是( )‎ 输入n 计算n(n＋1)‎ 输出结果 no yes ‎＞15‎ A．14 B．‎16 C．8＋ D．14＋‎ ‎【答案】C ‎9．（2014四川省内江市，9，3分）若关于x的一元二次方程(k－1) x 2＋2x－2＝0有不相等实数根，则k的取值范围是( )‎ A．k＞ B．k≥ C．k＞且k≠1 D．k≥且k≠1‎ ‎【答案】C ‎10．（2014四川省内江市，10，3分）如图4，Rt△ABC中，∠ACB＝90°，AC＝4，BC＝6，以斜边AB上的一点O为圆心所作的半圆分别与AC、BC相切于点D、E．则AD为( )‎ O B E C D A 图4‎ A．2.5 B．‎1.6 C．1.5 D．1‎ ‎【答案】B ‎11．（2014四川省内江市，11，3分）若关于x的方程m(x＋h)2＋k＝0(m、h、k均为常数，m≠0)的解是x1＝－3，x2＝2，则方程m(x＋h－3)2＋k＝0 ( )‎ A．x1＝－6，x2＝－1 B．x1＝0，x2＝5‎ C．x1＝－3，x2＝5 D．x1＝－6，x2＝2‎ ‎【答案】B ‎12．（2014四川省内江市，12，3分）如图5，已知A1、A2、……、An、An＋1是x轴上的点，且OA1＝A‎1A2＝A‎2A3＝……＝AnAn＋1＝1，分别过点A1、A2、……、An、An＋1作x轴的垂线交直线y＝2x于点B1、B2、……、Bn、Bn＋1，连接A1B2、B‎1A2、A2B3、B‎2A3、……、AnBn＋1、BnAn＋1，依次相交于点P1、P2、P3、……、Pn，△A1B1P1、△A2B2P2、……、△AnBnPn的面积依次为S1、S2、……、Sn，则Sn为( )‎ A1‎ A2‎ A3‎ A4‎ x ‎ y 图5‎ B1‎ B2‎ B3‎ B4‎ P1‎ P2‎ P3‎ A． B． C． D．‎ ‎【答案】D 二、填空题(本大题共4小题，每小题5分，共20分)‎ l3．（2014四川省内江市，13，5分）a－4ab2分解因式的结果是 ．‎ ‎【答案】a(1＋2b) (1－2b)‎ ‎14．（2014四川省内江市，14，5分）如图6，在四边形ABCD中，对角线AC、BD交于点O，AD∥BC，请添加一个条件： ，使四边形ABCD为平行四边形(不添加如何辅助线)．‎ ‎【答案】答案不唯一；AD＝BC；(或者AB∥DC)‎ ‎15．（2014四川省内江市，15，5分）有6张背面完全相同的卡片，每张正面分别画有三角形、平行四边形、矩形、正方形、梯形和圆，现将其全部正面朝下搅匀从中任取一张卡片，抽中正面画的图形是中心对称图形的概率为 ．‎ O A B C D 图6‎ ‎【答案】‎ ‎16．（2014四川省内江市，16，5分）如图7所示，将若干个正三角形、正方形和圆按一定规律从左向右排列，那么第2014个图形是 ．‎ ‎△△□□□△○○□□□△○○□□□△○○□……‎ ‎【答案】正方形 三、解答题（本大题共5小题，共44分，解答题应写出必要的文字说明或推演步骤．）‎ ‎17．（2014四川省内江市，17，8分）(本小题满分8分）‎ 计算：2tan60°－||－＋‎ ‎【答案】解：原式＝2＋－2－＋3＝1‎ ‎18．（2014四川省内江市，18，9分）(本小题满分9分）‎ 如图8，点M、N分别是正五边形ABCDE的边BC、CD上的点，且BM＝CN，AM交BN于点P．‎ ‎(1)求证：△ABM≌△BCN；‎ ‎(2)求∠APN的度数．‎ P M N C D E A B 图8‎ ‎【答案】‎ ‎(1)证明：∵五边形ABCDE是正五边形 ‎∴AB＝BC，∠ABM＝∠BCN 在△ABM和△BCN中 ‎ ‎∴△ABM≌△BCN(SAS)‎ ‎(2)解：∵△ABM≌△BCN ‎∴∠MBP＝∠BAP ‎∵∠MBP＋∠BMP＋∠BPM＝180°‎ ‎∠BAP＋∠BMA＋∠MBA＝180°‎ ‎∴∠BPM＝∠MBA ‎∵∠BPM＝∠APN ‎∴∠APN＝∠MBA＝＝108°．‎ ‎19．（2014四川省内江市，19，9分）(本小题满分9分）‎ 为推广阳光体育“大课间”活动，我市某中学决定在学生中开设A：实心球，B：立定跳远，C：跳绳，D：跑步四种活动项目．为了了解学生对四种项目的喜欢情况，随机抽取了部分学生进行调查，并将调査结果绘制成如图9①②的统计图．请结合图中的信息解答下列问题：‎ ‎(1)在这项调査中，共调査了多少名学生？‎ ‎(2)请计算本项调查中喜欢“立定跳远”的学生人数和所占百分比，并将两个统计图补充完整；‎ ‎(3)若调査到喜欢“跳绳”的5名学生中有3名男，2名女生．现从这5名学生中任意抽取2名学生，请用画树状图或列表的方法，求出刚好抽到同性别学生的概率．‎ ‎15‎ ‎45‎ ‎60‎ ‎30‎ D 人数 项目 B A C ‎75‎ ‎90‎ D ‎20%‎ B C ‎40%‎ A ‎10%‎ ‎15‎ ‎60‎ ‎30‎ ‎①‎ ‎②‎ 图9‎ ‎【答案】解：‎ ‎(1)在这项调査中，共调査的学生数是：‎ ‎15÷10%＝150 (名)‎ ‎(2) “立定跳远”的学生人数为：‎ ‎150－15－60－30＝45‎ ‎“立定跳远”的学生人数所占百分比为：‎ ‎100%－10%－40%－20%＝30%‎ 两个统计图补充完整如图所示；‎ ‎15‎ ‎45‎ ‎60‎ ‎30‎ D 人数 项目 B A C ‎75‎ ‎90‎ D ‎20%‎ B ‎30%‎ C ‎40%‎ A ‎10%‎ ‎15‎ ‎45‎ ‎60‎ ‎30‎ ‎②‎ 图9‎ ‎①‎ ‎(3)若调査到喜欢“跳绳”的5名学生中有3名男，2名女生．现从这5名学生中任意抽取2名学生，用列表的方法如下， ‎ 男1‎ 男2‎ 女1‎ 女2‎ 女3‎ 男1‎ ‎(男1，男2)‎ ‎(男1，女1)‎ ‎(男1，女2)‎ ‎(男1，女3)‎ 男2‎ ‎(男2，女1)‎ ‎(男2，女2)‎ ‎(男2，女3)‎ 女1‎ ‎(女1，女2)‎ ‎(女1，女3)‎ 女2‎ ‎(女2，女3)‎ 女3‎ 共有10种可能结果，其中刚好抽到同性别学生(记为事件A)的有4种：(男1，男2)，(女1，女2)，(女1，女3)，(女2，女3)，‎ 刚好抽到同性别学生的概率：P(A)＝‎ ‎20．（2014四川省内江市，20，9分）(本小题满分9分）‎ ‎“马航事件”的发生引起了我国政府的离度重视，迅速派出了舰船和飞机到相关海坡进行搜寻．如图10，在一次空中搜寻中，水平飞行的飞机现测得在点A俯角为30°方向的F点处有疑似飞机残骸的物体（该物体视为静止)．为了便于现察，飞机继续向前飞行了‎800米到达B点．此时测得点F在点B俯箱为45°的方向上．请你计算当飞机飞机F点的正上方点C时（点A、B、C在同一直线上），竖直离度CF约为多少米？（结果保留整数，料数值：≈1.7)‎ F C B A ‎30°‎ ‎45°‎ 图10‎ ‎【答案】解：‎ 如图：∠CBF＝45°∠BCF＝90°‎ ‎∴CF＝CB ‎∵∠A＝30°‎ ‎∴tan30°＝‎ ‎∵AB＝800‎ ‎∴‎ ‎∴CF＝400()≈1080．‎ 答：竖直离度CF约为‎1080米．‎ ‎21．（2014四川省内江市，21，9分）(本小题满分9分）‎ 如图11，一次函数y＝kx＋b的图象与反比例函数y＝(x＞0)的图象交于点P(n，2)，与x轴交于点A(－4，0)，与y轴交于点C，PB丄x轴于点B，且AC＝BC．‎ ‎(1)求一次函数、反比例函数的解析式；‎ ‎(2)反比例函数图象上是否存在点D，使四边形BCPD为菱形，如果存在，求出点D的坐标；如果不存在，说明理由．‎ A C P B x ‎ y O 图11‎ ‎【答案】解：(1)∵AC＝BC，CO⊥AB∴AO＝BO ‎∵A(－4，0)∴B(4，0)∴P(4，2)‎ 把P(4，2)代入y＝得m＝8,‎ ‎∴反比例函数的解析式：y＝‎ 把A(－4，0)，P(4，2)代入y＝kx＋b 得：解得：所以一次函数的解析式：y＝x＋1‎ ‎(2) 存在．‎ BC和AC关于y轴对称，所以BC的解析式为y＝－x＋1，向上平移2个单位，则y＝－x＋3， 与y＝联立方程的： 解得：x1＝16，x2＝－2(舍去)，所以D(16，)‎ 内江市2014年初中学业水平考试及高中阶段学校招生考试试卷 数学 B卷（共60分）‎ 四、填空题(本大题共4小题，每小题6分，共24分)‎ ‎22．（2014四川省内江市，22，6分）已知，则代数式的值为 ．‎ ‎【答案】‎ ‎23．（2014四川省内江市，23，6分）如图12，∠AOB＝30°，OP平分∠AOB，PC丄OB 于点C，若OC＝2，则PC的长是 ．‎ C B A P O 图12‎ ‎【答案】‎ ‎24．（2014四川省内江市，24，6分）已知实数x、y满足2x－3y＝4，并且x≥－1，y＜2，现有k＝x－y，则k的取值范围是 ．‎ ‎【答案】1≤k＜3‎ ‎25．（2014四川省内江市，25，6分）通过对课本中《硬币滚动中的数学》的学习，我们知道滚动圆滚动的周数取决于滚动圆的圆心运动的路程（如图13①)．在图13②中，有2014个半径为r的圆紧密排列成一条直线，半径为r的动圆C从图示位置绕这2014个圆排成的囝形无滑动地滚动一圈回到原位，则动圆C自身转动的周数为 ．‎ ‎……‎ C B A ‎①‎ ‎②‎ 图13‎ ‎【答案】1943‎ 五、解答题（本大题共3小题，每小题12分，共36分．解答应写出必要的文字说明或推演步骤．)‎ ‎26．（2014四川省内江市，26，12分）如图14，在∠ABC中，D是BC边上的点（不与点B、C重合），连结AD．‎ 问题引人：‎ ‎(1)如图14①，当点D是BC边上的中点时，S△ABD︰S△ABC＝ ；当点D是BC边上任意一点时，S△ABD︰S△ABC＝ (用图中已有线段表示）．‎ 探索研究：‎ ‎(2)如图14②，在△ABC中，O是线段AD上一点（不与点A、D重合），连结BO、CO，试猜想S△BOC与S△ABC之比应该等于图中哪两条线段之比，并说明理由．‎ 拓展应用：‎ ‎(3) 如图14③．O是线段AD上一点（不与点A、D重合），连接BO并延长交AC于点F，连接CO并延长交AB于点E．试猜想的值，并说明理由．‎ ‎①‎ D B C A ‎②‎ D B C A ‎③‎ D B C A 图14‎ O O E F ‎【答案】解：(1)1︰2；BD︰BC ‎(2) 猜想S△BOC与S△ABC之比应该等于OD︰AD D B C A O E F 证明：分别过O、A做BC的垂线OE、AF垂足为E、F．‎ ‎∴OE∥AF 所以OD︰AD＝OE︰AF ‎∴S△BOC＝ S△ABC＝‎ ‎∴S△BOC︰S△ABC＝︰＝OE︰AF＝OD︰AD ‎(3) 猜想的值是1．‎ 从(2)可知：‎ ‎27．（2014四川省内江市，27，12分）莱汽车销售公司经销某品牌A款汽车，随着汽车的普及，其价格也在不断下降．今年5月份A款汽车的售价比去年同间期每辆降价1万元，如果卖出相同数量的A款汽车，去年销售额为100万元，今年销售额只有90万元．‎ ‎(1)今年5月份A款汽车每辆售价多少万元？‎ ‎(2)为了增加收入，汽车销售公司决定再经销同品牌的B款汽车，已知A款汽车每辆进价7.5万元，B款汽车每辆进价为6万元，公司预计用不多于105万元且不少于99万元的资金购进这两款汽车共15辆，有几种进货方案？‎ ‎(3)如果B款汽车每辆售价为8万元，为打开B款汽车的销路，公用决定每售出一辆B款汽车，返还顾客现金a万元，要使（2)中所有方案获利相同，a值应是多少？此时，哪种方案对公司更有利？‎ ‎【答案】解：‎ ‎(1)设今年5月份A款汽车每辆售价x万元．根据题意得：‎ 解得：x＝9‎ 所以今年5月份A款汽车每辆售价9万元．‎ ‎(2)设A款汽车购进y辆．则B款汽车每辆购进(15－y)辆．根据题意得：‎ 解得：6≤y≤10，‎ 所以有5种方案：‎ 方案一：A款汽车购进6辆；B款汽车购进9辆 方案二：A款汽车购进7辆；B款汽车购进8辆 方案三：A款汽车购进8辆；B款汽车购进7辆 方案四：A款汽车购进9辆；B款汽车购进6辆 方案五：A款汽车购进10辆；B款汽车购进5辆 ‎ (3)设利润为W则：W＝(8－6)×(15－y)－a(15－y)＋(9－7.5)y＝30－2y－a(15－y)＋1.5y＝30－a(15－y)－0.5y 方案一：W＝30－a(15－6)－0.5×6＝30－‎9a－3＝27－‎‎9a 方案二：W＝30－a(15－7)－0.5×7＝30－‎8a－3.5＝26.5－‎‎8a 方案三：W＝30－a(15－8)－0.5×8＝30－‎7a－4＝26－‎‎7a 方案四：W＝30－a(15－9)－0.5×9＝30－‎6a－4.5＝25.5－‎‎6a 方案五：W＝30－a(15－10)－0.5×10＝30－‎5a－5＝25－‎‎5a 由27－‎9a＝26.5－‎8a 得a＝0.5‎ 方案一对公司更有利．‎ ‎28．（2014四川省内江市，28，12分）如图15，抛物线y＝ax2＋bx＋c经过点A(－3，0)、C(0，4)，‎ 点B在抛物线上，点B在抛物线上，CB∥x轴．且AB平分∠CAO．‎ ‎(1)求抛物线的解析式．‎ ‎(2)线段AB上有一动点P，过P作y轴的平行线，交拋物线于点Q，求线段PQ的最大值；‎ ‎(3)抛物线的对称轴上是否存在点M，使△ABM是以AB为直角边的直角三角形？如果存在，求出点M的坐标；如果不存在，说明理由．‎ O C B x ‎ y A ‎【答案】解：‎ ‎(1) A(－3，0)、C(0，4)，所以AC＝5‎ ‎∵AB平分∠CAO ‎∴∠CAB＝∠BAO ‎∵CB∥x轴 ‎∴∠CBA＝∠BAO ‎∴∠CAB＝∠CBA ‎∴AC＝BC＝5‎ ‎∴B(5，4)‎ A(－3，0)、C(0，4)、B(5，4)代入y＝ax2＋bx＋c得：‎ 解得： 所以y＝x2＋x＋4‎ ‎(2) 设AB的解析式为：y＝kx＋b 把A(－3，0)、B(5，4)代入解得：所以解析式为：y＝x＋；可设P(x，x＋)，Q(x，x2＋x＋4)，则PQ＝x2＋x＋4－(x＋)＝；当时，PQ最大．且最大值为．‎ O C B x ‎ y A P Q ‎(3) y＝x2＋x＋4的对称轴是x＝，要使△ABM是以AB为直角边的直角三角形，有两种情况：‎ ‎①以B为直角顶点．AB的解析式为：y＝x＋，则BM的解析式为y＝x＋b，把B(5，4‎ ‎)代入得4＝×5＋b，所以b＝，BM的解析式为y＝x＋，解得：，即M的坐标(，2)‎ ‎②以A为直角顶点．AB的解析式为：y＝x＋，则BM的解析式为y＝x＋b，把A(－3，0)代入得0＝×(－3)＋b，所以b＝，BM的解析式为y＝x，解得：，即M的坐标(，)‎ O C B x ‎ y A x＝‎ M1‎ M2‎