- 2021-04-16 发布 |
- 37.5 KB |
- 8页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
黔西南州市2015中考数学卷
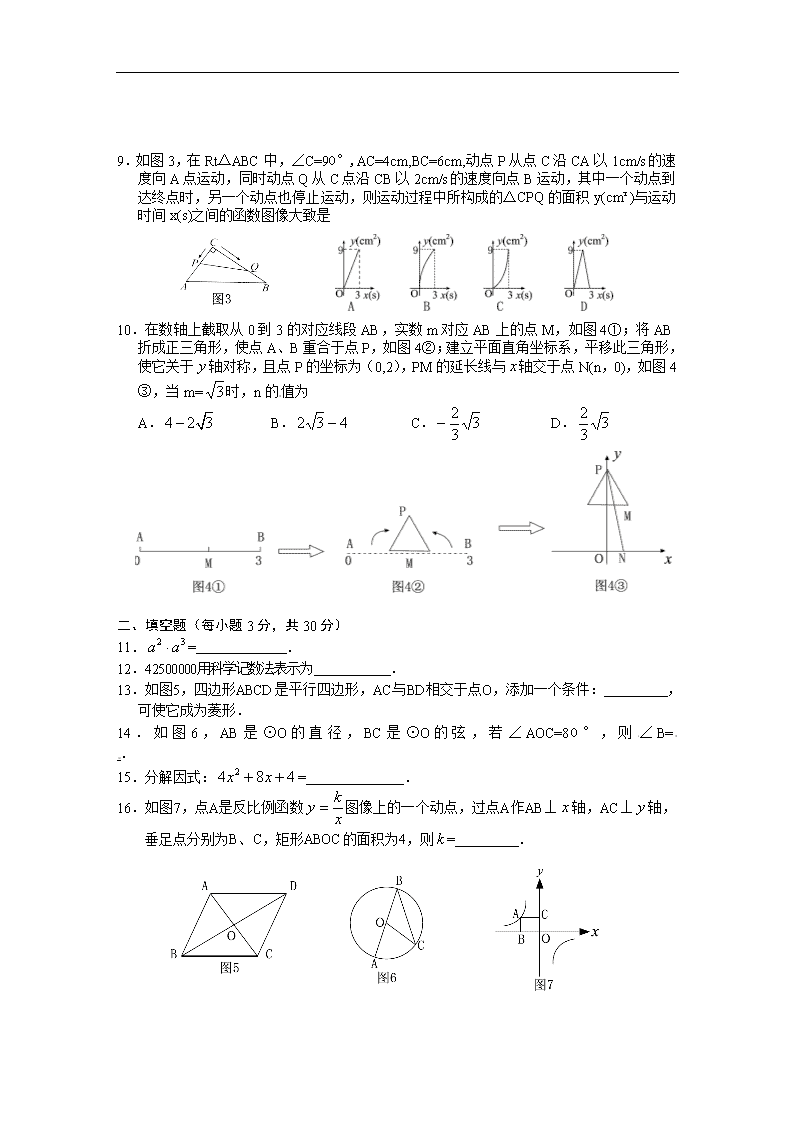
秘密★启用前 黔西南州2015年初中毕业生学业暨升学统一考试试卷 数 学 考生注意: 1.一律用黑色笔或2B铅笔将答案填写或填涂在答题卷指定位置内。 2.本试卷共4页,满分150分,答题时间120分钟。 一、选择题(每小题4分,共40分) 1.下列各数是无理数的是 A. B. C. D. 2.分式有意义,则的取值范围是 A. B. C. D.一切实数 3.如图1,在菱形ABCD中,AC与BD相交于点O,AC=8,BD=6,则菱形的边长AB等于 A.10 B. C.6 D.5 4.已知一组数据:-3,6,2,-1,0,4,则这组数据的中位数是 A.1 B. C.0 D.2 5.已知△∽△且,则为 A.1:2 B.2:1 C.1:4 D.4:1 6.如图2,点P在⊙O外,PA、PB分别与⊙O相切于A、B两点,∠P=50°,则∠AOB等于 A.150° B.130° C.155° D.135° 7.某校准备修建一个面积为180平方米的矩形活动场地,它的长比宽多11米,设场地的宽为米,则可列方程为 A. B. C. D. 8.下面几个几何体,主视图是圆的是 A B C D 9.如图3,在Rt△ABC中,∠C=90°,AC=4cm,BC=6cm,动点P从点C沿CA以1cm/s的速度向A点运动,同时动点Q从C点沿CB以2cm/s的速度向点B运动,其中一个动点到达终点时,另一个动点也停止运动,则运动过程中所构成的△CPQ的面积y(cm²)与运动时间x(s)之间的函数图像大致是 10.在数轴上截取从0到3的对应线段AB,实数m对应AB上的点M,如图4①;将AB折成正三角形,使点A、B重合于点P,如图4②;建立平面直角坐标系,平移此三角形,使它关于轴对称,且点P的坐标为(0,2),PM的延长线与轴交于点N(n,0),如图4③,当m=时,n的值为 A. B. C. D. 二、填空题(每小题3分,共30分) 11.= . 12.42500000用科学记数法表示为 . 13.如图5,四边形ABCD是平行四边形,AC与BD相交于点O,添加一个条件: ,可使它成为菱形. 14.如图6,AB是⊙O的直径,BC是⊙O的弦,若∠AOC=80°,则∠B= . 15.分解因式:= . 16.如图7,点A是反比例函数图像上的一个动点,过点A作AB⊥轴,AC⊥轴,垂足点分别为B、C,矩形ABOC的面积为4,则= . 17.已知圆锥的底面圆半径为3,母线长为5,则圆锥的侧面积是 . 18.已知,则= . 19.如图8,AB是⊙O的直径,CD为⊙O的一条弦,CD⊥AB于点E,已知CD=4,AE=1,则⊙O的半径为 . 20.已知=3×2=6,=5×4×3=60,=5×4×3×2=120, =6×5×4×3=360,依此规律= . 三、(本题共12分) 21.(1)计算: (2)解方程:. 四、(本题共12分) 22.如图9所示,点O在∠APB的平分线上,⊙O与PA相切于点C. (1)求证:直线PB与⊙O相切 (2)PO的延长线与⊙O交于点E,若⊙O的半径为3,PC=4. 求弦CE的长. 五、(本题共14分) 23.为了提高中学生身体素质,学校开设了A:篮球、B:足球、C:跳绳、D:羽毛球四种体育活动,为了解学生对这四种体育活动的喜欢情况,在全校随机抽取若干名学生进行问卷调查(每个被调查的对象必须选择而且只能在四种体育活动中选择一种),将数据进行整理并绘制成以下两幅统计图10(未画完整). (1)这次调查中,一共调查了 名学生; (2)请补全两幅统计图; (3)若有3名喜欢跳绳的学生,1名喜欢足球的学生组队外出参加一次联谊活动,欲从中选出2人担任组长(不分正副),求一人是喜欢跳绳、一人是喜欢足球的学生的概率. 六、(本题共14分) 24.某地为了鼓励居民节约用水,决定实行两级收费制,即每月用水量不超过12吨(含12吨)时,每吨按政府补贴优惠价收费;每月超过12吨,超过部分每吨按市场调节价收费,小黄家1月份用水24吨,交水费42元.2月份用水20吨,交水费32元. (1)求每吨水的政府补贴优惠价和市场调节价分别是多少元; (2)设每月用水量为吨,应交水费为元,写出与之间的函数关系式; (3)小黄家3月份用水26吨,他家应交水费多少元? 七、阅读材料题(本题共12分) 25.求不等式的解集. 解:根据“同号两数相乘,积为正”可得:① 或 ②. 解①得;解②得. ∴不等式的解集为或. 请你仿照上述方法解决下列问题: (1)求不等式的解集. (2)求不等式的解集. 八、(本题共16分) 26.如图11,在平面直角坐标系中,平行四边形如图放置,将此平行四边形绕点O顺时针旋转90°得到平行四边形.抛物线经过点A、C、A′三点. (1)求A、A′、C三点的坐标; (2)求平行四边形和平行四边形重叠部分的面积; (3)点M是第一象限内抛物线上的一动点,问点M在何处时,的面积最大?最大面积是多少?并写出此时M的坐标. 黔西南州2015年初中毕业生学业暨升学统一考试试卷 数学参考答案及评分标准 一、选择题(每小题4分,共40分) 1.C 2.B 3. D 4.A 5. C 6. B 7. C 8. B 9. C 10. A 二、填空题(每小题3分,共30分) 11. 12. 4.25×107 13. AC⊥BD 14. 40° 15. 16. -4 17. 18. 2 19. 20. 840 三、21.题(本题共两个小题,每小题6分,共12分) (1)解:原式=1+1-2+2……………………………………………………………(4分) =…………………………………………………………………(6分) (2)解:去分母得: ……………………………………………(2分) ………………………………………………………………………(3分) ………………………………………………………………………(4分) 检验:把代入()≠0,∴是原分式方程的解 ………………(6分) 四、22题(每小题6分,共12分) (1)证明:过点O作OD⊥PB,连接OC. …………(2分) ∵AP与⊙O相切, ∴OC⊥AP. ……………………(3分) 又∵OP平分∠APB, ∴OD=OC.……………………(4分) ∴PB是⊙O的切线. …………………………………(6分) (2)解:过C作CF⊥PE于点F.……………………………………………………(1分) 在Rt△OCP中,OP=……………………………………………(2分) ∵ ∴ ……………………………………………………………………(3分) 在Rt△COF中, ∴ 在Rt△CFE中,………………………………………(6分) 五、23题(3+4+7分,共14分) (1)200…………………………………………………………………………………(3分) (2)如图 ………………………………………………………………………………(4分) (3)用表示喜欢跳绳的学生,用B表示喜欢足球的学生,列表如下 第 一 人 第 二 人 C1 C2 C3 B C1 (C2 ,C1) (C3 ,C1) (B, C1) C2 (C1 ,C2) (C3 ,C2) (B, C2) C3 (C1,C3) (C2 ,C3) (B, C3) B (C1 ,B) (C2 ,B) (C3 ,B) ……………………………………………………………………(4分) ∴P(一人是喜欢跳绳,一人是喜欢足球的学生)=………………………………(7分) 六、24题(本题5+5+4共14分) 解:(1)设每吨水的政府补贴优惠价和市场调节价分别为x元,y元.依题意得………(1分) ……………………………………………………………(3分) 解方程组得: ………………………………………………………(4分) 答:每吨水的政府补贴优惠价1元, 市场调节价2.5元 …………………(5分) (2)当x≤12时,y=x; ………………………………………………………………(2分) 当x>12时,y=12+2.5(x-12) 即y=2.5x-18. …………………………………………………………………(5分) (3)当x=26时,y=2.5×26-18=65-18=47(元) ……………………………(3分) 答:小黄家三月份应交水费47元. …………………………………(4分) 七、25题(每小题6分,共12分) (1)根据“异号两数相乘,积为负”可得 ① 或 ② ……………………………(3分) 解不等式组①得无解,解不等式组②得 ………………………………(4分) ∴原不等式的解集为 ……………………………………………(6分) (2)依题意可得① 或 ②……………………………(3分) 解①得x≥3,解②得x<-2………………………………………………………(4分) ∴原不等式的解集为x≥3或x<-2……………………………………………(6分) 八、26题(本题4+6+6分,共16分) (1)解:(1)当时,……………………………………… (1分) 解得……………………………………………………………(3分) ∴C(-1,0),A′(3,0).当x=0时,y=3.∴A(0,3) ……………………………(4分) (2)∵C(-1,0),A(0,3) , ∴B(1,3) ∴ ………………………………………………………………(1分) ∴△AOB的面积为 ………………………………………………(2分) 又∵平行四边形ABOC旋转得平行四边形A′B′OC′,∴∠ACO=∠OC′D 又∵∠ACO=∠ABO,∴∠ABO=∠OC′D. 又∵∠C′OD=∠AOB, ∴△ C′OD ∽△BOA …………………………………………………………(4分) ∴ ……………………………………………………(5分) ∴ ………………………………………………………………(6分) (3)设M点的坐标为(),连接OM ……………………(1分) ……………(3分) = …………………………………………(4分) 当时,取到最大值为 ………………………………(5分) ∴M() ………………………………………………(6分)查看更多