高考数学 数列专题复习
专题一 数列
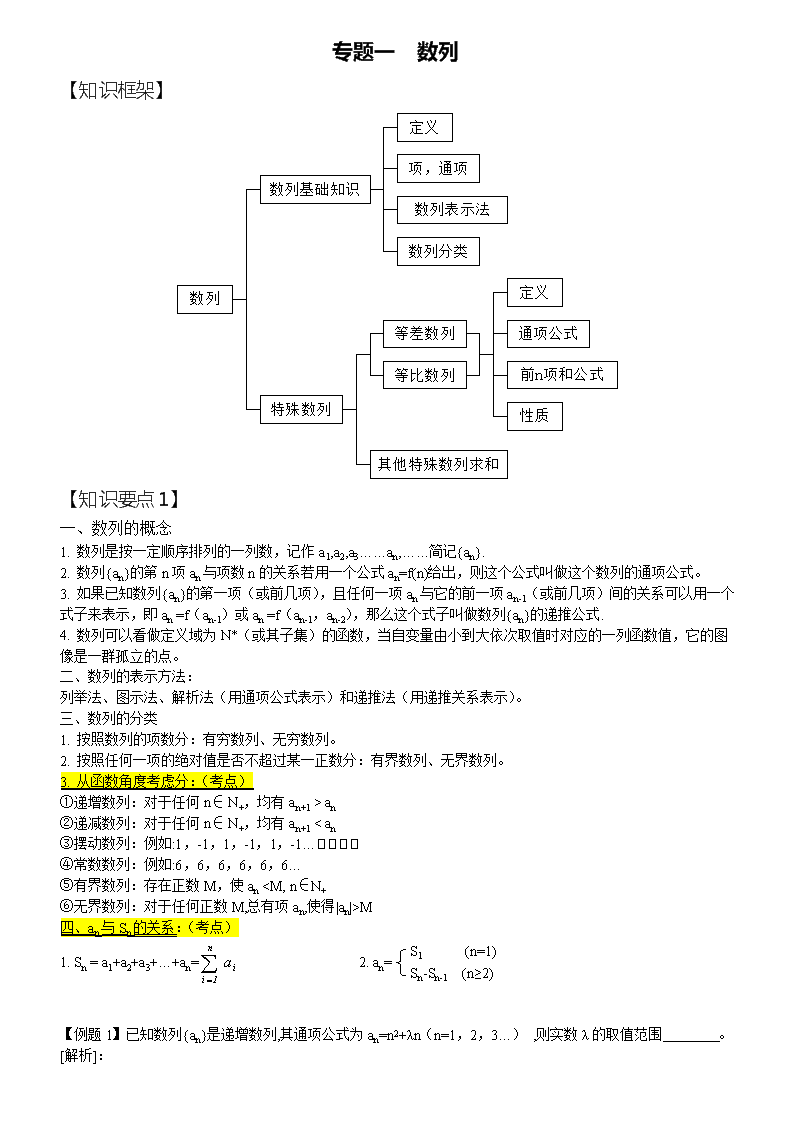
【知识框架】
【知识要点1】
一、数列的概念
1. 数列是按一定顺序排列的一列数,记作a1,a2,a3……an,……简记{an}.
2. 数列{an}的第n项an与项数n的关系若用一个公式an=f(n)给出,则这个公式叫做这个数列的通项公式。
3. 如果已知数列{an}的第一项(或前几项),且任何一项an与它的前一项an-1(或前几项)间的关系可以用一个式子来表示,即an =f(an-1)或an =f(an-1,an-2),那么这个式子叫做数列{an}的递推公式.
4. 数列可以看做定义域为N*(或其子集)的函数,当自变量由小到大依次取值时对应的一列函数值,它的图像是一群孤立的点。
二、数列的表示方法:
列举法、图示法、解析法(用通项公式表示)和递推法(用递推关系表示)。
三、数列的分类
1. 按照数列的项数分:有穷数列、无穷数列。
2. 按照任何一项的绝对值是否不超过某一正数分:有界数列、无界数列。
3. 从函数角度考虑分:(考点)
①递增数列:对于任何n∈ N+,均有an+1 > an
②递减数列:对于任何n∈ N+,均有an+1 < an
③摆动数列:例如:1,-1,1,-1,1,-1…L---
④常数数列:例如:6,6,6,6,6,6…
⑤有界数列:存在正数M,使an
M
S1 (n=1)
Sn-Sn-1 (n≥2)
四、an与Sn的关系:(考点)
1. Sn = a1+a2+a3+…+an= 2. an=
【例题1】已知数列{an}是递增数列,其通项公式为an=n2+λn(n=1,2,3…) ,则实数λ的取值范围 。
[解析]:
∵数列{an}的通项公式为an=n2+λn(n=1,2,3…) 数列是递增数列
∴an+1-an=(n+1)2+λ(n+1)- n2-λn
=2n+1+λ>0 恒成立
∵2n+1+λ的最小值是3+λ ∴3+λ>0 ∴λ>-3 实数λ的取值范围是(-3,+∞)
【例题2】数列{an}的通项公式为an=3n2-28n,则数列各项中最小项是( B )
A.第4项 B.第5项 C.第6项 D.第7项
[解析1]:an=f(n)= 3n2-28n,f(n)是一元二次函数,其图像开口向上,有最低点,最低点是
由于n∈ N+,故取n=4和n=5代入,得到a4=-64,a5=-65,故选择B
an≥an-1
an≤an+1
3n2-28n≥3(n-1)2-28(n-1)
3n2-28n≤3(n+1)2-28(n+1)
[解析2]:
设an为数列的最小项,则有 代入化简得到
解得: 故n=5
【练习1】在数列1,1,2,3,5,8,x,21,34,55中,x的值为( D )
-2 (n=1)
2n-5 (n≥2)
A.10 B.11 C.12 D.13
【练习2】数列{an}的前n项和Sn=n2-4n+1,则an an=
【知识要点2等差数列】
1. 定义:如果数列{an}从第二项起每一项与它的前一项的差等于同一个常数,那么这个数列叫做等差数列,这个常数叫等差数列的公差。即an-an-1=d(n∈N+,且n≥2),或者an+1-an=d(n∈N+)
2. 通项公式:
an=a1+(n-1)d an=am+(n-m)d (公式的变形) an=an+b 其中a=d,b= a1-d
3. 前n项和公式:
(公式的变形) Sn=An2+Bn 其中A= B=
4. 性质:
(1)公式变形
(2)如果A=,那么A叫做a和b的等差中项.
(3)若{}为等差数列,且有k+l=m+n, 则
(4)若为等差数列则{是等差数列,其中p,q均为常数
(5)若{}为等差数列,则(k,m)组成公差为md的等差数列.
(6)若分别为{}的前n项,前2m项,前3m项的和,则,,成等差数列.
(7)若{}设等差数列,则是等差数列,其首项与{}首项相同,公差是{}公差的
(7)非零等差数列奇数项与偶数项的性质
若项数为2n,则S偶-S奇=nd, 若项数为2n-1,则S偶=(n-1)an,S奇=nan,
5. 判断:
①定义法:an+1-an=d(n∈N+)
② 中项法: 2an+1=an+ an+2 +=Û {}为等差数列。
③通项公式法:an=an+b(a,b为常数)Û{ }
④前n项和公式法:Sn=An2+Bn(A,B为常数)Û{}
【例题1】已知是公差为1的等差数列,为的前项和,若,则( B )
(A) (B) (C) (D)
[解析]:∵ d=1 ∴S8=8a1+28 S4=4a1+6
∵S8=4 S4 ∴ a1=0.5 an=a1+(n-1)d ∴a10=
【例题2】在等差数列中,若,则= 10 .
[解析]:因为是等差数列,所以,即,所以,故应填入.
【知识要点3等比数列】
1. 定义:如果一个数列从第二项起,每一项与它的前一项的比等于同一个不为零的常熟,那么这个数列就叫做等比数列.这个常熟叫做等比数列的公比,通常用字母q表示,及
2. 通项公式:
na1 (q=1)
或 (q≠1)
如果等比数列的公比为q,那么它的通项公式为.
3. 前n项和公式:
设等比数列{}的公比为q,其前n项和=
4. 性质:
(1)
等比数列{}满足或时,{}是递增数列;
满足或时,{}是递减数列.
当q=1时,{}为常数数列;
当q<0时,{}为摆动数列,且所有奇数项与同号,所有偶数项与异号.
(2)对于正整数m,n,p,q,若m+n=p+q,则在等比数列{}中,的关系为:
(3)若{},{}为等比数列(项数相同),则{}(≠0),{},{},{},{}仍是等比数列.
(4)如果a,G,b成等比数列,那么G叫做a与b的等比中项,且G=±√ab。不是任何两数都有等比中项,只
有同号两数才存在等比中项,且有两个等比中项。
【例题1】已知数列是递增的等比数列,,则数列的前项和等于 .
[解析]:由题意解得:a1=1,a4=8, q=2,那么
【例题2】数列中为的前n项和,若,则 6 .
[解析]:∵an+1=2an ∴数列是等比数列,q=2
∵Sn= =126 其中a1=2 ∴n=6
【知识要点4】★(大题)
一、考点1:求an:
1. 归纳法(由特殊到一般即找规律)
由于归纳法求解通项的题目一般在选择填空常见,较少出现在大题中。
2. 利用Sn与an的关系求通项公式
由Sn求an时,要分n=1和n≥2两种情况讨论,然后验证两种情况能否用统一的式子表示。若不能,则分段表示.
2. 由递推关系求数列的通项公式【累加法、累乘法、待定系数法、阶差法(逐差法)、迭代法、对数变换法、倒数变换法、换元法(目的是去递推关系式中出现的根号)、数学归纳法、不动点法(递推式是一个数列通项的分式表达式)、特征根法】
1.累加法:若已知且则,即.
2.累乘法:若已知且则 ,即
3.换元法:若已知且且p)则令,可得{}(其中)为等比数列,其中可用待定系数法求出.
【例题1】已知数列满足,求数列的通项公式。(累加法)
解:由得则
所以数列的通项公式为。
【例题2】已知数列满足,求数列的通项公式。(累乘法)
解:因为,所以,则,故
所以数列的通项公式为
二、考点2:求Sn:
1.公式法:直接用等差、等比数列的求和公式求解
2.倒序相加法:在数列{}中,与首末两端等“距离”的两项和相等或可构成能求和的新数列,可用倒序相加法求此数列的前n项和。(此法在实际解体过程中并不常用,例子:等差数列前n项和公式推导)
3.错位相减法:在数列{}中,{}是等差数列,{}是等比数列,可用错位相减法求此数列的前n项和.
4.裂项相消法:把数列的每一项拆成两项之差,求和时有些部分可以相互抵消,从而达到求和的目的.
5.分组转化求和法:
若一个数列的通项公式是由若干个等差数列或等比数列组成,则求和时可用分组转化法分别求和再相加减。即把复杂的通项公式求和的任务转化为简单的等差和等比的求和。
6.并项求和法:一个数列的前n项和中,可两两结合求解,则称之为并项求和.形如类型,可采用两项合并求解.
【例题1】设数列满足 ,(1)求数列的通项公式;(2)令,求数列的前n项和。(错位相减法)
[解析]:(1)由已知,当n≥1时,
。 而 所以数列{}的通项公式为。
(2)由知
①
从而
②
① -②得
即
【例题2】求数列的前n项和。(裂项相消法)
[解析]:设 (裂项)
则 (裂项求和)
=
=