- 2021-04-16 发布 |
- 37.5 KB |
- 6页

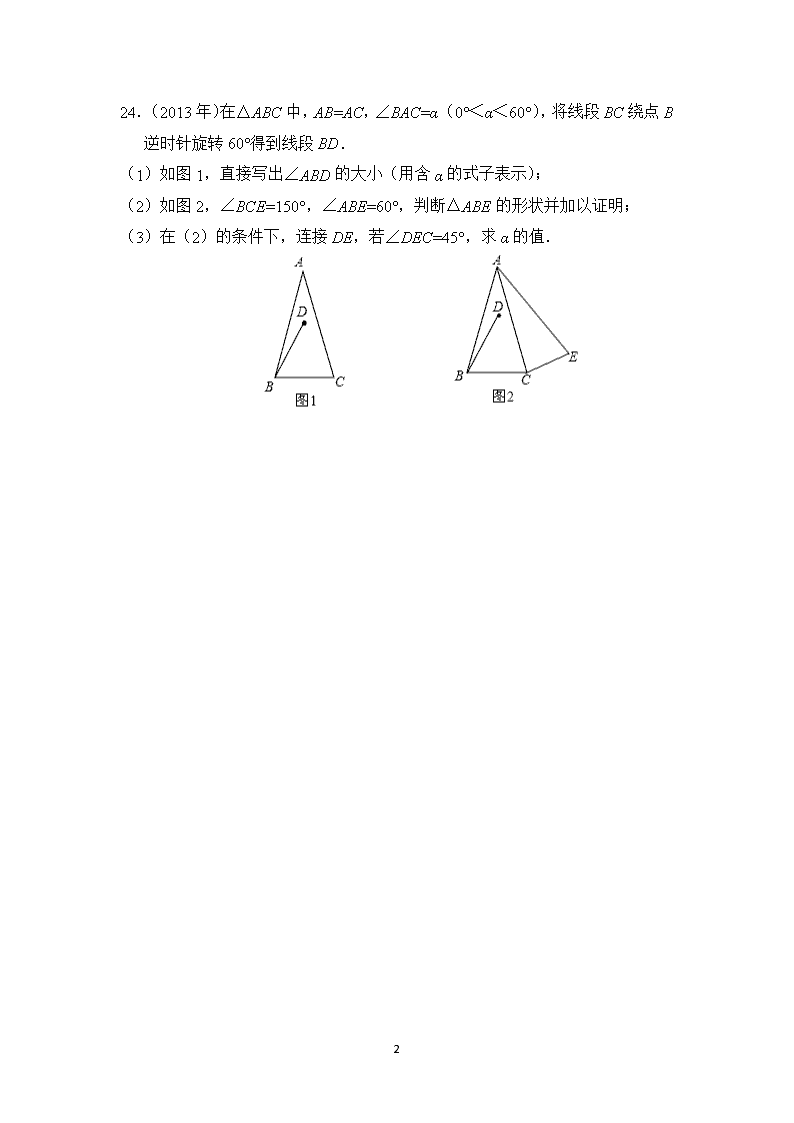
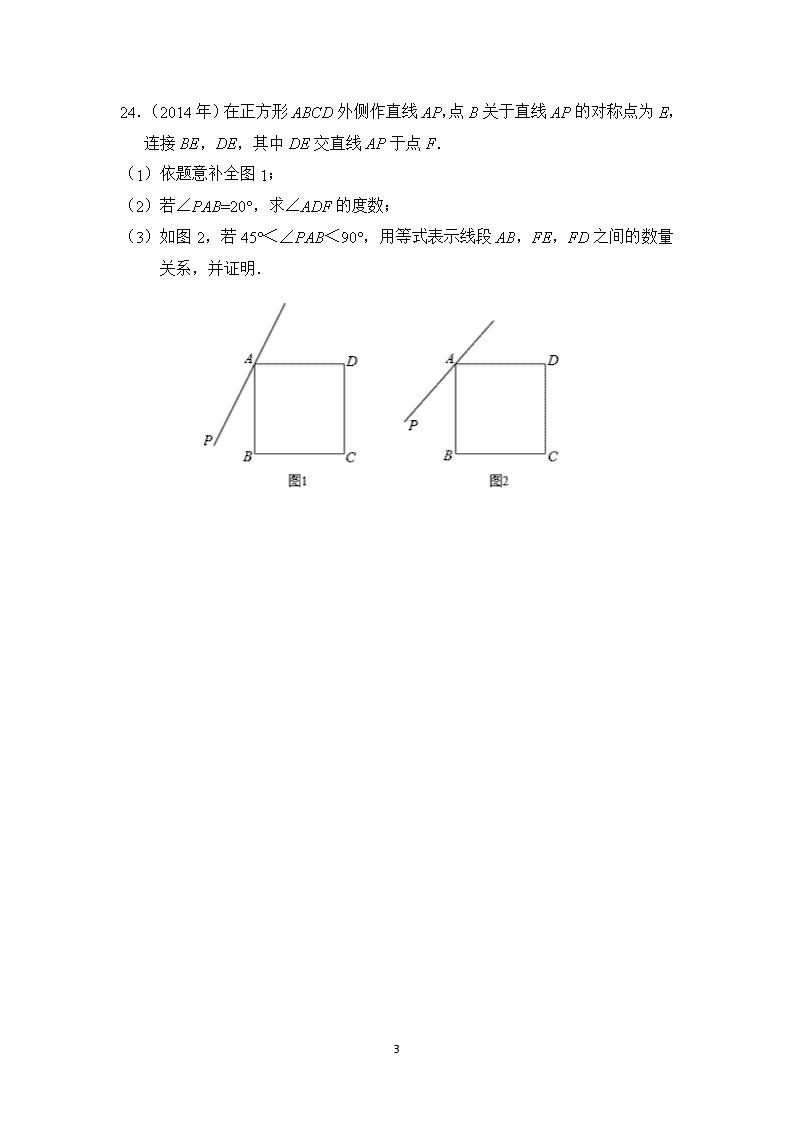
申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2012北京市中考几何综合题
24.(2012年)在△ABC中,BA=BC,∠BAC=α,M是AC的中点,P是线段BM上的动点,将线段PA绕点P顺时针旋转2α得到线段PQ. (1)若α=60°且点P与点M重合(如图1),线段CQ的延长线交射线BM于点D,请补全图形,并写出∠CDB的度数; (2)在图2中,点P不与点B,M重合,线段CQ的延长线于射线BM交于点D,猜想∠CDB的大小(用含α的代数式表示),并加以证明; (3)对于适当大小的α,当点P在线段BM上运动到某一位置(不与点B,M重合)时,能使得线段CQ的延长线与射线BM交于点D,且PQ=QD,请直接写出α的范围. 6 24.(2013年)在△ABC中,AB=AC,∠BAC=α(0°<α<60°),将线段BC绕点B逆时针旋转60°得到线段BD. (1)如图1,直接写出∠ABD的大小(用含α的式子表示); (2)如图2,∠BCE=150°,∠ABE=60°,判断△ABE的形状并加以证明; (3)在(2)的条件下,连接DE,若∠DEC=45°,求α的值. 6 24.(2014年)在正方形ABCD外侧作直线AP,点B关于直线AP的对称点为E,连接BE,DE,其中DE交直线AP于点F. (1)依题意补全图1; (2)若∠PAB=20°,求∠ADF的度数; (3)如图2,若45°<∠PAB<90°,用等式表示线段AB,FE,FD之间的数量关系,并证明. 6 28.(2015年)在正方形ABCD中,BD是一条对角线,点P在射线CD上(与点C、D不重合),连接AP,平移△ADP,使点D移动到点C,得到△BCQ,过点Q作QH⊥BD于H,连接AH,PH. (1)若点P在线段CD上,如图1. ①依题意补全图1; ②判断AH与PH的数量关系与位置关系并加以证明; (2)若点P在线段CD的延长线上,且∠AHQ=152°,正方形ABCD的边长为1,请写出求DP长的思路.(可以不写出计算结果) 6 28.(2016年)在等边△ABC中, (1)如图1,P,Q是BC边上的两点,AP=AQ,∠BAP=20°,求∠AQB的度数; (2)点P,Q是BC边上的两个动点(不与点B,C重合),点P在点Q的左侧,且AP=AQ,点Q关于直线AC的对称点为M,连接AM,PM. ①依题意将图2补全; ②小茹通过观察、实验提出猜想:在点P,Q运动的过程中,始终有PA=PM,小茹把这个猜想与同学们进行交流,通过讨论,形成了证明该猜想的几种想法: 想法1:要证明PA=PM,只需证△APM是等边三角形; 想法2:在BA上取一点N,使得BN=BP,要证明PA=PM,只需证△ANP≌△PCM; 想法3:将线段BP绕点B顺时针旋转60°,得到线段BK,要证PA=PM,只需证PA=CK,PM=CK… 请你参考上面的想法,帮助小茹证明PA=PM(一种方法即可). 6 28.(2017年)在等腰直角△ABC中,∠ACB=90°,P是线段BC上一动点(与点B、C不重合),连接AP,延长BC至点Q,使得CQ=CP,过点Q作QH⊥AP于点H,交AB于点M. (1)若∠PAC=α,求∠AMQ的大小(用含α的式子表示). (2)用等式表示线段MB与PQ之间的数量关系,并证明. 6查看更多