- 2021-04-16 发布 |
- 37.5 KB |
- 15页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
八年级下册数学同步练习第六章复习2 北师大版
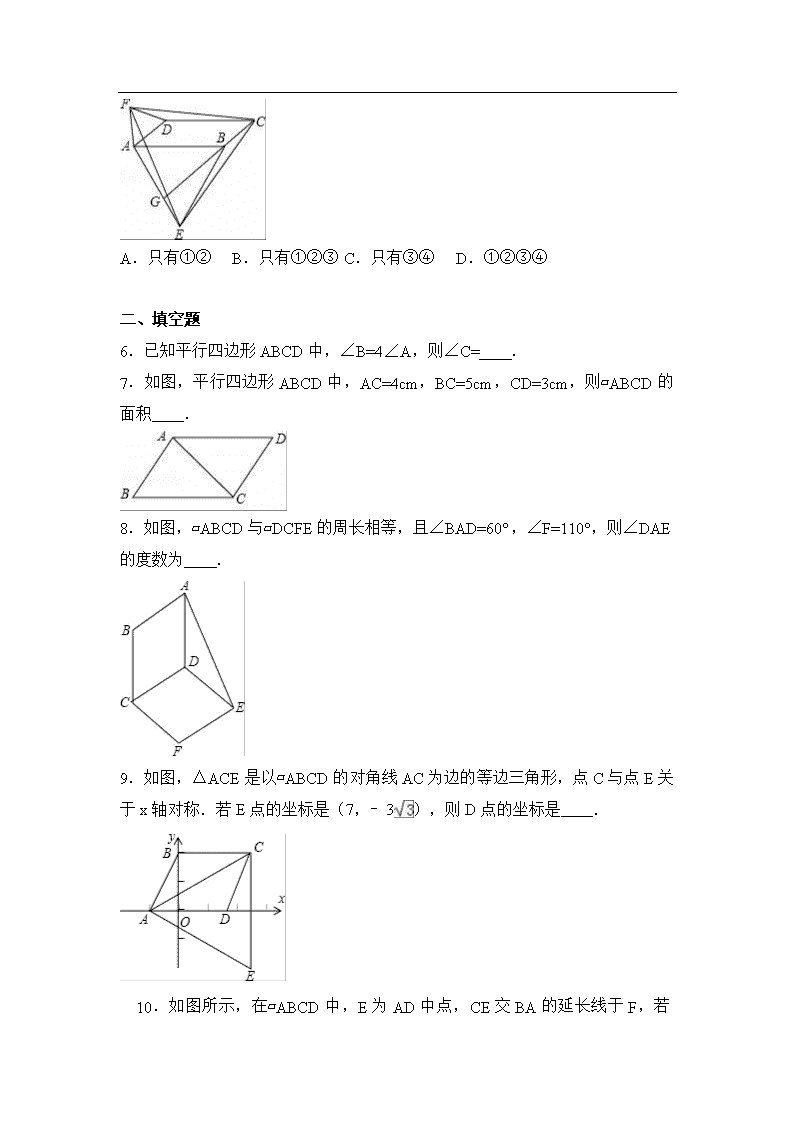
第六章复习 一、选择题 1.已知▱ABCD的周长为32,AB=4,则BC=( ) A.4 B.12 C.24 D.28 2.在平行四边形ABCD中,∠B=60°,那么下列各式中,不能成立的是( ) A.∠D=60° B.∠A=120° C.∠C+∠D=180° D.∠C+∠A=180° 3.如图,在平行四边形ABCD中,AB>BC,按以下步骤作图:以A为圆心,小于AD的长为半径画弧,分别交AB、CD于E、F;再分别以E、F为圆心,大于EF的长半径画弧,两弧交于点G;作射线AG交CD于点H.则下列结论: ①AG平分∠DAB,②CH=DH,③△ADH是等腰三角形,④S△ADH=S四边形ABCH. 其中正确的有( ) A.①②③ B.①③④ C.②④ D.①③[来源:学_科_网] 4.在△MNB中,BN=6,点A,C,D分别在MB,NB,MN上,四边形ABCD为平行四边形,且∠NDC=∠MDA,则四边形ABCD的周长是( ) A.24 B.18 C.16 D.12 5.如图,在▱ABCD中,分别以AB、AD为边向外作等边△ABE、△ADF,延长CB交AE于点G,点G在点A、E之间,连接CE、CF,EF,则以下四个结论一定正确的是( ) ①△CDF≌△EBC;②∠CDF=∠EAF;③△ECF是等边三角形;④CG⊥AE. [来源:学科网ZXXK] A.只有①② B.只有①②③ C.只有③④ D.①②③④ 二、填空题 6.已知平行四边形ABCD中,∠B=4∠A,则∠C= . 7.如图,平行四边形ABCD中,AC=4cm,BC=5cm,CD=3cm,则▱ABCD的面积 . 8.如图,▱ABCD与▱DCFE的周长相等,且∠BAD=60°,∠F=110°,则∠DAE的度数为 . 9.如图,△ACE是以▱ABCD的对角线AC为边的等边三角形,点C与点E关于x轴对称.若E点的坐标是(7,﹣3),则D点的坐标是 . 10.如图所示,在▱ABCD中,E为AD中点,CE交BA的延长线于F,若BC=2AB,∠FBC=70°,则∠EBC的度数为 度. 三、解答题 11.如图,已知平行四边形ABCD,DE是∠ADC的角平分线,交BC于点E. (1)求证:CD=CE; (2)若BE=CE,∠B=80°,求∠DAE的度数. 12.已知:如图,在▱ABCD中,∠ADC、∠DAB的平分线DF、AE分别与线段BC相交于点F、E,DF与AE相交于点G. (1)求证:AE⊥DF; (2)若AD=10,AB=6,AE=4,求DF的长. 参考答案与试题解析 一、选择题 1.已知▱ABCD的周长为32,AB=4,则BC=( ) A.4 B.12 C.24 D.28 【考点】平行四边形的性质. 【专题】计算题. 【分析】根据平行四边形的性质得到AB=CD,AD=BC,根据2(AB+BC)=32,即可求出答案. 【解答】解:∵四边形ABCD是平行四边形, ∴AB=CD,AD=BC, ∵平行四边形ABCD的周长是32, ∴2(AB+BC)=32, ∴BC=12. 故选B. 【点评】本题主要考查对平行四边形的性质的理解和掌握,能利用平行四边形的性质进行计算是解此题的关键. 2.在平行四边形ABCD中,∠B=60°,那么下列各式中,不能成立的是( ) A.∠D=60° B.∠A=120° C.∠C+∠D=180° D.∠C+∠A=180° 【考点】平行四边形的性质;多边形内角与外角. 【专题】压轴题. 【分析】由于平行四边形中相邻内角互补,对角相等,而∠A和∠C是对角,而它们和∠B是邻角,∠D和∠B是对角,由此可以分别求出它们的度数,然后可以判断了. 【解答】解:∵四边形ABCD是平行四边形, ∴∠A=∠C,∠B=∠D, 而∠B=60°, ∴∠A=∠C=120°,∠D=60°. 所以D是错误的. 故选D. 【点评】本题主要利用了平行四边形的角的性质解决问题. 3.如图,在平行四边形ABCD中,AB>BC,按以下步骤作图:以A为圆心,小于AD的长为半径画弧,分别交AB、CD于E、F;再分别以E、F为圆心,大于EF的长半径画弧,两弧交于点G;作射线AG交CD于点H.则下列结论: ①AG平分∠DAB,②CH=DH,③△ADH是等腰三角形,④S△ADH=S四边形ABCH.[来源:Z,xx,k.Com] 其中正确的有( ) A.①②③ B.①③④ C.②④ D.①③ 【考点】平行四边形的性质;作图—复杂作图. 【分析】根据作图过程可得得AG平分∠DAB;再根据角平分线的性质和平行四边形的性质可证明∠DAH=∠DHA,进而得到AD=DH,从而得到△ADH是等腰三角形. 【解答】解:根据作图的方法可得AG平分∠DAB, 故①正确; ∵AG平分∠DAB, ∴∠DAH=∠BAH, ∵CD∥AB, ∴∠DHA=∠BAH, ∴∠DAH=∠DHA, ∴AD=DH, ∴△ADH是等腰三角形, 故③正确; 故选:D. 【点评】此题主要考查了平行四边形的性质,以及角平分线的做法,关键是掌握平行四边形对边平行. 4.在△MNB中,BN=6,点A,C,D分别在MB,NB,MN上,四边形ABCD为平行四边形,且∠NDC=∠MDA,则四边形ABCD的周长是( ) A.24 B.18 C.16 D.12 【考点】平行四边形的性质. 【分析】本题利用了平行四边形的性质,两组对边分别平行,利用两直线平行得出同位角相等后,再根据已知条件判断出BM=BN,从而四边形ABCD的周长=BM+BN=2BN而求解. 【解答】解:在平行四边形ABCD中CD∥AB,AD∥BC, ∴∠M=∠NDC,∠N=∠MDA, ∵∠NDC=∠MDA, ∴∠M=∠N=∠NDC=∠MDA, ∴MB=BN=6,CD=CN,AD=MA, ∴四边形ABCD的周长=AB+BC+CD+AD=MA+AB+BC+CN=MB+BN=2BN=12. 故选D. 【点评】要求周长就要先求出四边的长,要求四边的长,就要根据平行四边形的性质和已知条件计算. 5.如图,在▱ABCD中,分别以AB、AD为边向外作等边△ABE、△ ADF,延长CB交AE于点G,点G在点A、E之间,连接CE、CF,EF,则以下四个结论一定正确的是( ) ①△CDF≌△EBC;②∠CDF=∠EAF;③△ECF是等边三角形;④CG⊥AE. A.只有①② B.只有①②③ C.只有③④ D.①②③④ 【考点】平行四边形的性质;全等三角形的判定与性质;等边三角形的性质;等边三角形的判定. 【专题】压轴题. 【分析】根据题意,结合图形,对选项一一求证,判定正确选项. 【解答】解:∵△ABE、△ADF是等边三角形 ∴FD=AD,BE=AB ∵AD=BC,AB=DC ∴FD=BC,BE=DC ∵∠B=∠D,∠FDA=∠ABE ∴∠CDF=∠EBC ∴△CDF≌△EBC,故①正确; ∵∠FAE=∠FAD+∠EAB+∠BAD=60°+60°+(180°﹣∠CDA)=300°﹣∠CDA, ∠FDC=360°﹣∠FDA﹣∠ADC=300°﹣∠CDA, ∴∠CDF=∠EAF,故②正确; 同理可得:∠CBE=∠EAF=∠CDF, ∵BC=AD=AF,BE=AE, ∴△EAF≌△EBC, ∴∠AEF=∠BEC, ∵∠AEF+∠FEB=∠BEC+∠FEB=∠AEB=60°, ∴∠FEC=60°, ∵CF=CE, ∴△ECF是等边三角形,故③正确; 在等边三角形ABE中, ∵等边三角形顶角平分线、底边上的中线、高和垂直平分线是同一条线段 ∴如果CG⊥AE,则G是AE的中点,∠ABG=30°,∠ABC=150°,题目缺少这个条件,CG⊥AE不能求证,故④错误. 故选B. 【点评】本题考查了全等三角形的判定、等边三角形的判定和性质、平行四边形的性质等知识,综合性强.考查学生综合运用数学知识的能力. 二、填空题 6.已知平行四边形ABCD中,∠B=4∠A,则∠C= 36° . 【考点】平行四边形的性质. 【分析】首先利用平行四边形性质得到∠C=∠A,BC∥AD,推出∠A+∠B=180°,求出∠A的度数,即可求出∠C. 【解答】解:∵四边形ABCD是平行四边形, ∴∠C=∠A,BC∥AD, ∴∠A+∠B=180°, ∵∠B=4∠A, ∴∠A=36°, ∴∠C=∠A=36°, 故答案为36°. 【点评】本题考查了平行四边形性质和平行线的性质的应用,主要考查学生运用平行四边形性质进行推理的能力,题目比较好,难度也不大. 7.如图,平行四边形ABCD中,AC=4cm,BC=5cm,CD=3cm,则▱ABCD的面积 12cm2 . 【考点】平行四边形的性质. 【分析】利用勾股定理的逆定理可知△ABC是直角三角形,再利用平行四边形的面积等于2倍的△ABC的面积计算即可. 【解答】解:∵四边形ABCD是平行四边形, ∴AB=CD=3cm, ∵AC=4cm,BC=5cm, ∴AC2+AB2=AC2, ∴△ABC是直角三角形, ∴S△ABC=×3×4=6cm2, ∴则▱ABCD的面积=2×6=12cm2, 故答案为12cm2. 【点评】本题考查了勾股定理的逆定理和平行四边形的性质,题目比较简单. 8.如图,▱ABCD与▱DCFE的周长相等,且∠BAD=60°,∠F=110°,则∠DAE的度数为 25° . 【考点】平行四边形的性质. 【专题】压轴题. 【分析】由,▱ABCD与▱DCFE的周长相等,可得到AD=DE即△ADE是等腰三角形,再由且∠BAD=60°,∠F=110°,即可求出∠DAE的度数. 【解答】解:∵▱ABCD与▱DCFE的周长相等,且CD=CD, ∴AD=DE, ∵∠DAE=∠DEA, ∵∠BAD=60°,∠F=110°, ∴∠ADC=120°,∠CDE═∠F=110°, ∴∠ADE=360°﹣120°﹣110°=130°, ∴∠DAE==25°, 故答案为:25°. 【点评】本题考查了平行四边形的性质:平行四边形的对边相等、平行四边形的对角相等以及邻角互补和等腰三角形的判定和性质、三角形的内角和定理. 9.如图,△ACE是以▱ABCD的对角线AC为边的等边三角形,点C与点E关于x轴对称.若E点的坐标是(7,﹣3),则D点的坐标是 (5,0) . 【考点】平行四边形的性质;坐标与图形性质;等边三角形的性质. 【专题】压轴题. 【分析】设CE和x轴交于H,由对称性可知CE=6,再根据等边三角形的性质可知AC=CE=6,根据勾股定理即可求出AH的长,进而求出AO和DH的长,所以OD可求,又因为D在x轴上,纵坐标为0,问题得解.[来源:学.科.网] 【解答】解:∵点C与点E关于x轴对称,E点的坐标是(7,﹣3), ∴C的坐标为(7,3), ∴CH=3,CE=6, ∵△ACE是以▱ABCD的对角线AC为边的等边三角形, ∴AC=6, ∴AH=9, ∵OH=7, ∴AO=DH=2, ∴OD=5,[来源:学§科§网Z§X§X§K] ∴D点的坐标是(5,0), 故答案为(5,0). 【点评】本题考查了平行四边形的性质、等边三角形的性质、点关于x轴对称的特点以及勾股定理的运用. 10.如图所示,在▱ABCD中,E为AD中点,CE交BA的延长线于F,若BC=2AB,∠FBC=70°,则∠EBC的度数为 35 度. 【考点】平行四边形的性质. 【分析】由题意可证△DEC≌△AEF,从而推出BC=BF,即△FBC为等腰三角形,E为FCR的中点,所以得到∠EBC=∠EBF=∠CBF=35°. 【解答】解:∵▱ABCD, ∴AB=CD,DC∥AB, ∴∠ECD=∠EFA ∵DE=AE,∠DEC=∠AEF ∴△DEC≌△AEF ∴DC=AF ∴AB=AF ∵BC=2AB,AB=AF ∴BC=BF ∴△FBC为等腰三角形 再由△DEC≌△AEF,得EC=EF ∴∠EBC=∠EBF=∠CBF=×70°=35° 故答案为35. 【点评】本题主要考查了平行四边形的性质,题目给出了一角,求未知角,这就要根据已知的条件,让已知与未知建立联系,求出角. 三、解答题 11.如图,已知平行四边形ABCD,DE是∠ADC的角平分线,交BC于点E. (1)求证:CD=CE; (2)若BE=CE,∠B=80°,求∠DAE的度数. 【考点】平行四边形的性质. 【专题】计算题;证明题. 【分析】(1)根据DE是∠ADC的角平分线得到∠1=∠2,再根据平行四边形的性质得到∠1=∠3,所以∠2=∠3,根据等角对等边即可得证; (2)先根据BE=CE结合CD=CE得到△ABE是等腰三角形,求出∠BAE的度数,再根据平行四边形邻角互补得到∠BAD=100°,所以∠DAE可求. 【解答】(1)证明:如图,在平行四边形ABCD中, ∵AD∥BC ∴∠1=∠3 又∵∠1=∠2, ∴∠2=∠3, ∴CD=CE; (2)解:∵四边形ABCD是平行四边形, ∴AB=CD,AD∥BC, 又∵CD=CE,BE=CE, ∴AB=BE, ∴∠BAE=∠BEA. ∵∠B=80°, ∴∠BAE=50°, ∴∠DAE=180°﹣50°﹣80°=50°. 【点评】(1)由角平分线得到相等的角,再利用平行四边形的性质和等角对等边的性质求解; (2)根据“BE=CE”得出AB=BE是解决问题的关键. 12.已知:如图,在▱ABCD中,∠ADC、∠DAB的平分线DF、AE分别与线段BC相交于点F、E,DF与AE相交于点G. (1)求证:AE⊥DF; (2)若AD=10,AB=6,AE=4,求DF的长. 【考点】平行四边形的性质;垂线;平行线的性质;三角形内角和定理;角平分线的性质;勾股定理. 【专题】几何综合题. 【分析】(1)根据平行四边形的性质和平行线的性质推出∠ADC+∠DAB=180°,根据角平分线得到∠ADF+∠DAE=(∠ADC+∠DAB)=90°,即可求出结论; (2)过点D作DH∥AE,交BC的延长线于点H,得到平行四边形AEHD,求出DH=AE=4,EH=AD=10,根据平行四边形的性质和平行线的性质推出DC=FC,AB=EB,求出BF、FE、FH的长,根据勾股定理即可求出答案. 【解答】(1)证明:在▱ABCD中AB∥CD, ∴∠ADC+∠DAB=180°. ∵DF、AE分别是∠ADC、∠DAB的平分线, ∴∠ADF=∠CDF=∠ADC,∠DAE=∠BAE=∠DAB, ∴∠ADF+∠DAE=(∠ADC+∠DAB)=90°, ∴∠AGD=90°, ∴AE⊥DF; (2)解:过点D作DH∥AE,交BC的延长线于点H, 则四边形AEHD是平行四边形,且FD⊥DH. ∴DH=AE=4,EH=AD=10. 在▱ABCD中AD∥BC, ∴∠ADF=∠CFD,∠DAE=∠BEA. ∴∠CDF=∠CFD,∠BAE=∠BEA. ∴DC=FC,AB=EB. 在▱ABCD中,AD=BC=10,AB=DC=6, ∴CF=BE=6,BF=BC﹣CF=10﹣6=4. ∴FE=BE﹣BF=6﹣4=2, ∴FH=FE+EH=12, 在Rt△FDH中,DF===8. 答:DF的长是8. 【点评】本题主要考查对平行四边形的性质,勾股定理,三角形的内角和定理,平行线的性质,角平分线的定义,垂线的定义等知识点的理解和掌握,熟练地运用这些性质进行证明是解此题的关键,题型较好,综合性强. 查看更多