- 2021-04-16 发布 |
- 37.5 KB |
- 5页
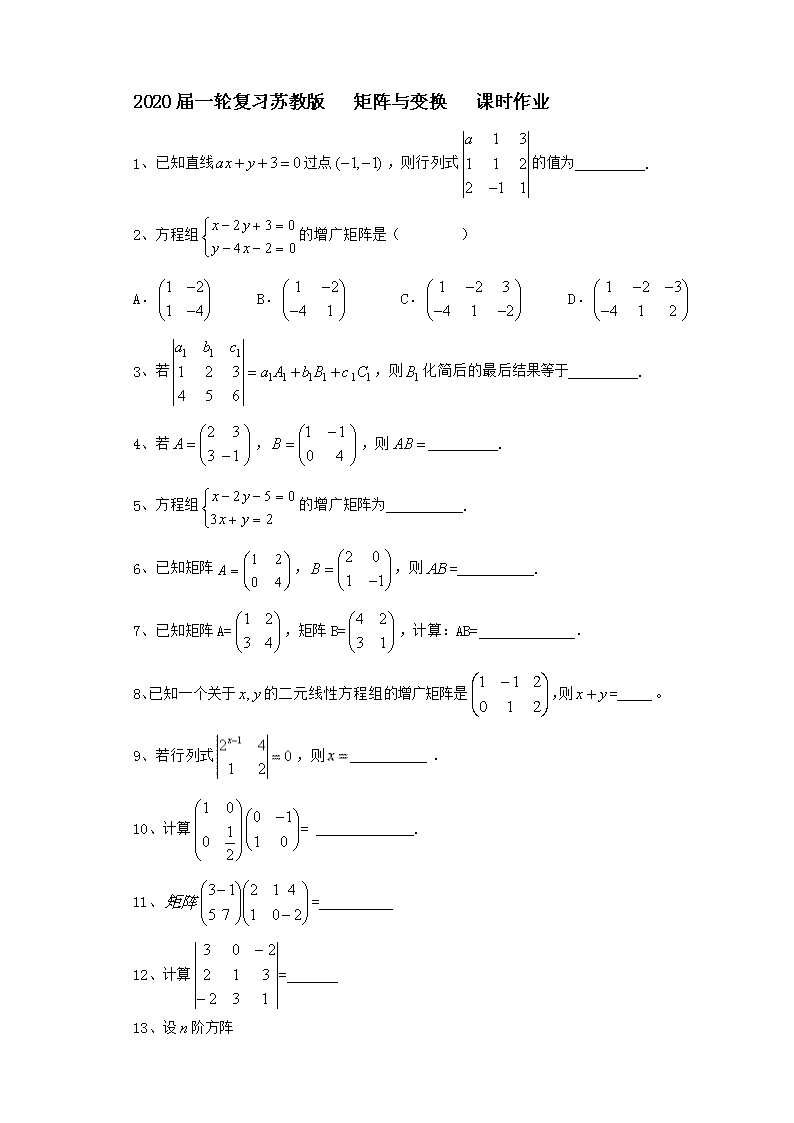

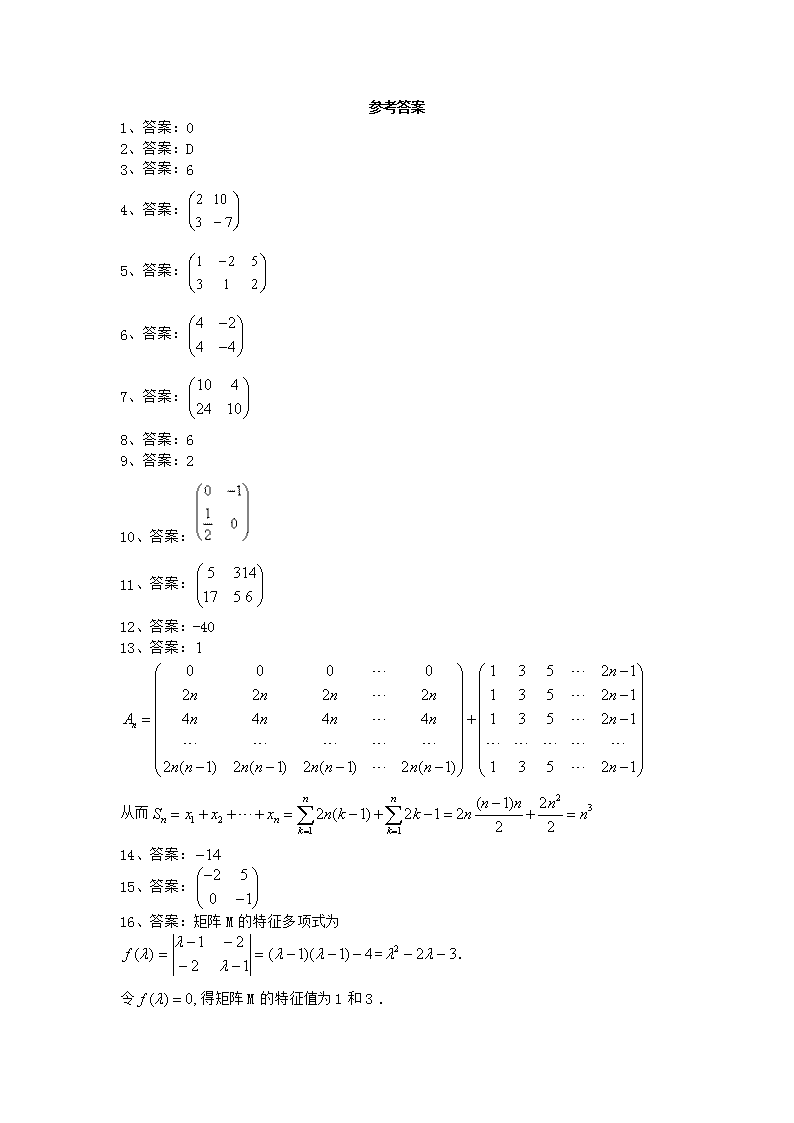
申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
【数学】2020届一轮复习苏教版 矩阵与变换 课时作业
2020届一轮复习苏教版 矩阵与变换 课时作业 1、已知直线过点,则行列式的值为__________. 2、方程组的增广矩阵是( ) A. B. C. D. 3、若,则化简后的最后结果等于__________. 4、若,,则__________. 5、方程组的增广矩阵为___________. 6、已知矩阵,,则=___________. 7、已知矩阵A=,矩阵B=,计算:AB= . 8、已知一个关于的二元线性方程组的增广矩阵是,则=_____。 9、若行列式,则___________. 10、计算= ______________. 11、= 12、计算= 13、设阶方阵 , 任取中的一个元素,记为;划去所在的行和列,将剩下的元素按原来的位置关系组成阶方阵,任取中的一个元素,记为;划去所在的行和列,……;最后剩下一个元素记为,记,则=__________. 14、行列式中第行第列元素的代数余子式的值为,则实数=__________. 15、已知矩阵,,则=__________. 16、求矩阵M=的特征值及其对应的特征向量. 17、在直角坐标系中,已知的顶点坐标为,求在矩阵对应的变换下所得到的图形的面积,这里矩阵 18、已知矩阵.(1)求逆矩阵; (2)若矩阵X满足,试求矩阵X. 19、二阶矩阵有特征值其对应的一个特征向量并且矩阵对应的变换将点变换成点,求矩阵. 20、解关于的方程组,并对解的情况进行讨论. 参考答案 1、答案:0 2、答案:D 3、答案:6 4、答案: 5、答案: 6、答案: 7、答案: 8、答案:6 9、答案:2 10、答案: 11、答案: 12、答案:-40 13、答案: 从而 14、答案: 15、答案: 16、答案:矩阵M的特征多项式为=. 令得矩阵M的特征值为1和3 . 当 所以矩阵M的属于特征值1的一个特征向量为. 当 所以矩阵M的属于特征值3的一个特征向量为. 17、答案:方法一:由题设得 由 可知三点在矩阵对应的变换下所得到的点分别是计算得的面积为l.所以△ABC在矩阵对应的变换下所得到的图形的面积为1. 方法二:在矩阵对应的变换下,一个图形变换为其绕原点逆时针旋转得到的图形;在矩阵作用下,一个图形变换为与之关于直线对称的图形.因此,在矩阵对应的变换下所得到的图形,与全等.从而其面积等于△ABC的面积,即为l. 18、答案:(1)设=,则==. ∴解得∴=. (2). 19、答案:设,则由,得, 即 由,得, 从而, 由,,解得 ∴, 20、答案:,, 当且,即,方程组有唯一解; 当,即,,方程组有无穷多解,; 当,即,,方程组无解. 查看更多