- 2021-04-15 发布 |
- 37.5 KB |
- 9页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2010中考数学绍兴考试试题
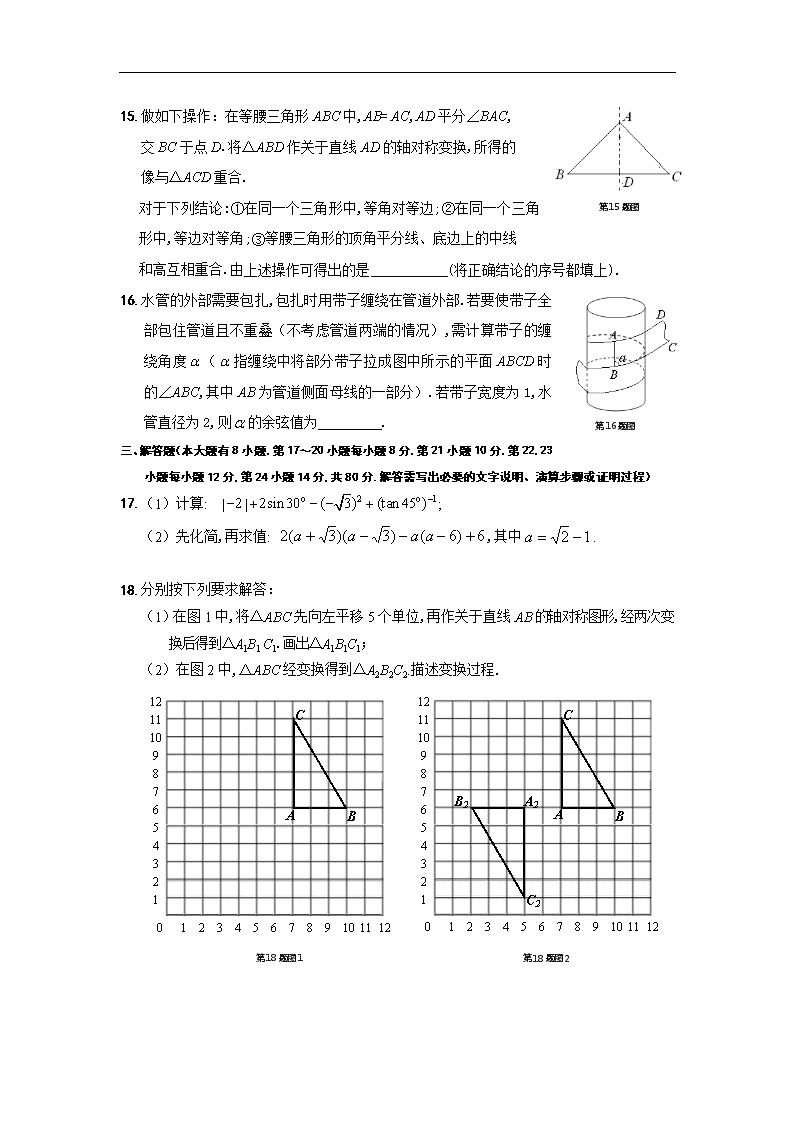
2010年浙江省绍兴市初中毕业生学业考试试卷 数 学 一、选择题(本大题有10小题,每小题4分,共40分.请选出每小题中一个符合题意的正确选项,不选、多选、错选,均不给分) 1.的相反数是( ) A.2 B.-2 C. D. 主视方向 2.如图,是由四个相同的小正方体组成的立体图形,它的俯视图是( ) A. B. C. D. 第2题图 3.已知⊙O的半径为5,弦AB的弦心距为3,则AB的长是( ) A.3 B.4 C.6 D.8 第4题图 4.自上海世博会开幕以来,中国馆以其独特的造型吸引 了世人的目光.据预测,在会展期间,参观中国馆的人次数估计可达到14 900 000,此数用科学记数法表示是 ( ) A. B. C. D. 5.化简,可得( ) A. B. C. D. 6.甲、乙、丙、丁四位选手各10次射击成绩的平均数和方差如下表: 选 手 甲 乙 丙 丁 平均数(环) 9.2 9.2 9.2 9.2 方差(环2) 0.035 0.015 0.025 0.027 则这四人中成绩发挥最稳定的是( ) A.甲 B.乙 C.丙 D.丁 第7题图 7.一辆汽车和一辆摩托车分别从A,B两地去同一城市,它们离A地的路程随时间变化的图象如图所示.则下列结论错误的是( ) A.摩托车比汽车晚到1 h B. A,B两地的路程为20 km C.摩托车的速度为45 km/h D.汽车的速度为60 km/h 第8题图 B A C 8.如图,已知△ABC,分别以A,C为圆心,BC,AB长为半径画弧,两弧在直线BC上方交于点D,连结AD,CD.则有( ) A.∠ADC与∠BAD相等 B.∠ADC与∠BAD互补 C.∠ADC与∠ABC互补 D.∠ADC与∠ABC互余 9.已知(x1, y1),(x2, y2),(x3, y3)是反比例函数的图象上的三个点,且x1<x2<0,x3>0,则y1,y2,y3的大小关系是( ) A. y3<y1<y2 B. y2<y1<y3 C. y1<y2<y3 D. y3<y2<y1 第10题图 A B 单位:mm l1 l2 10.如图为某机械装置的截面图,相切的两圆⊙O1, ⊙O2均与⊙O的弧AB相切,且O1O2∥l1( l1为水 平线),⊙O1,⊙O2的半径均为30 mm,弧AB的 最低点到l1的距离为30 mm,公切线l2与l1间的 距离为100 mm.则⊙O的半径为( ) A.70 mm B.80 mm C.85 mm D.100 mm 二、填空题(本大题有6小题,每小题5分,共30分.将答案填在题中第12题图 横线上) 11.因式分解:=_______________. 12.如图,⊙O是正三角形的外接圆,点在劣弧上, =22°,则的度数为_____________. 13.不等式-的解是_______________. 14.根据第六届世界合唱比赛的活动细则,每个参赛的合唱团在比赛时须演唱4首歌曲.爱乐合唱团已确定了2首歌曲,还需在A,B两首歌曲中确定一首,在C,D两首歌曲中确定另一首,则同时确定A,C为参赛歌曲的概率是_______________. 15.做如下操作:在等腰三角形ABC中,AB= AC,AD平分∠BAC, 交BC于点D.将△ABD作关于直线AD的轴对称变换,所得的 像与△ACD重合. 第15题图 对于下列结论:①在同一个三角形中,等角对等边;②在同一个三角形中,等边对等角;③等腰三角形的顶角平分线、底边上的中线 和高互相重合.由上述操作可得出的是 (将正确结论的序号都填上). 第16题图 16.水管的外部需要包扎,包扎时用带子缠绕在管道外部.若要使带子全部包住管道且不重叠(不考虑管道两端的情况),需计算带子的缠绕角度(指缠绕中将部分带子拉成图中所示的平面ABCD时的∠ABC,其中AB为管道侧面母线的一部分).若带子宽度为1,水管直径为2,则的余弦值为 . 三、解答题(本大题有8小题,第17~20小题每小题8分,第21小题10分,第22,23小题每小题12分,第24小题14分,共80分.解答需写出必要的文字说明、演算步骤或证明过程) 17.(1)计算: ||; (2)先化简,再求值: ,其中. 18.分别按下列要求解答: (1)在图1中,将△ABC先向左平移5个单位,再作关于直线AB的轴对称图形,经两次变换后得到△A1B1 C1.画出△A1B1C1; (2)在图2中,△ABC经变换得到△A2B2C2.描述变换过程. 0 1 2 3 4 5 6 7 8 9 10 12 11 12 11 10 9 8 7 6 5 4 3 2 1 A B C A2 B2 C2 0 1 2 3 4 5 6 7 8 9 10 12 11 12 11 10 9 8 7 6 5 4 3 2 1 A B C 第18题图2 第18题图1 19.绍兴有许多优秀的旅游景点,某旅行社对5月份本社接待的外地游客来绍旅游的首选景点作了一次抽样调查,调查结果如下图表. 人数(人) 景点 外地游客来绍旅游首选景点统计图 鲁迅故里 柯岩胜景 五泄瀑布 大佛寺院 千丈飞瀑 曹娥庙宇 其它 外地游客来绍旅游首选景点的频数分布表 景点 频数 频率 鲁迅故里 650 0.325 柯岩胜景 350 五泄瀑布 300 0.15 大佛寺院 300 0.15 千丈飞瀑 200 0.1 曹娥庙宇 0.075 其 它 50 0.025 第19题图 (1)请在上述频数分布表中填写空缺的数据,并补全统计图; (2)该旅行社预计6月份接待外地来绍的游客2 600人,请你估计首选景点是鲁迅故里的人数. 20.如图,小敏、小亮从A,B两地观测空中C处一个气球,分 别测得仰角为30°和60°,A,B两地相距100 m.当气球 沿与BA平行地飘移10秒后到达C′处时,在A处测得气 球的仰角为45°. (1)求气球的高度(结果精确到0.1m); 第20题图 (2)求气球飘移的平均速度(结果保留3个有效数字). A y O B x 第21题图 21.在平面直角坐标系中,一次函数的图象与坐标轴围成的三角形, 叫做此一次函数的坐标三角形.例如,图中的一次函数的图象与 x,y轴分别交于点A,B,则△OAB为此函数的坐标三角形. (1)求函数y=x+3的坐标三角形的三条边长; (2)若函数y=x+b(b为常数)的坐标三角形周长为16, 求此三角形面积. 22.某公司投资新建了一商场,共有商铺30间.据预测,当每间的年租金定为10万元时,可全部租出.每间的年租金每增加5 000元,少租出商铺1间.该公司要为租出的商铺每间每年 交各种费用1万元,未租出的商铺每间每年交各种费用5 000元. (1)当每间商铺的年租金定为13万元时,能租出多少间? (2)当每间商铺的年租金定为多少万元时,该公司的年收益(收益=租金-各种费用)为275万元? 23. (1) 如图1,在正方形ABCD中,点E,F分别在边BC, CD上,AE,BF交于点O,∠AOF=90°. 求证:BE=CF. 第23题图1 (2) 如图2,在正方形ABCD中,点E,H,F,G分别在边AB, BC,CD,DA上,EF,GH交于点O,∠FOH=90°, EF =4.求GH的长. 第23题图2 (3) 已知点E,H,F,G分别在矩形ABCD的边AB,BC,CD,DA上,EF,GH交于点O, ∠FOH=90°,EF=4. 直接写出下列两题的答案: ①如图3,矩形ABCD由2个全等的正方形组成,求GH的长; ②如图4,矩形ABCD由n个全等的正方形组成,求GH的长(用n的代数式表示). 第23题图4 第23题图3 24.如图,设抛物线C1:, C2:,C1与C2的交点为A, B,点A的坐标是,点B的横坐标是-2. 第24题图 (1)求的值及点B的坐标; (2)点D在线段AB上,过D作x轴的垂线,垂足为点H, 在DH的右侧作正三角形DHG. 记过C2顶点M的 直线为,且与x轴交于点N. ① 若过△DHG的顶点G,点D的坐标为 (1, 2),求点N的横坐标; ② 若与△DHG的边DG相交,求点N的横 坐标的取值范围. 浙江省2010年初中毕业生学业考试绍兴市试卷数学参考答案 一、选择题(本大题有10小题,满分40分) 1.D 2.C 3. D 4. D 5.B 6.B 7.C 8. B 9. A 10. B 二、填空题(本大题有6小题,满分30分) 11. 12. 38° 13. 14. 15.②③ 16. 第18题图 三、解答题(本大题有8小题,满分80分) 17.(本题满分8分) 解:(1) 原式= 2+1-3+1=1. (2) 原式=, 当时,原式=. 18.(本题满分8分) (1) 如图. (2) 将△ABC先关于点A作中心对称图形,再向左平移 第20题图 第21题图 2个单位,得到△A2B2C2.(变换过程不唯一) 19.(本题满分8分) (1) 0.175, 150. 图略. (2) 解:2 600×0.325=845(人) . 20.(本题满分8分) 解:(1) 作CD⊥AB,C/E⊥AB,垂足分别为D,E. ∵ CD =BD·tan60°, CD =(100+BD)·tan30°, ∴(100+BD)·tan30°=BD·tan60°, ∴ BD=50, CD =50≈86.6 m, ∴ 气球的高度约为86.6 m. (2) ∵ BD=50, AB=100, ∴ AD=150 , 又∵ AE =C/E=50, ∴ DE =150-50≈63.40, ∴ 气球飘移的平均速度约为6.34米/秒. 21.(本题满分10分) 解:(1) ∵ 直线y=x+3与x轴的交点坐标为(4,0),与y轴交点坐标为(0,3), ∴函数y=x+3的坐标三角形的三条边长分别为3,4,5. (2) 直线y=x+b与x轴的交点坐标为(,0),与y轴交点坐标为(0,b), 当b>0时,,得b =4,此时,坐标三角形面积为; 当b<0时,,得b =-4,此时,坐标三角形面积为. 综上,当函数y=x+b的坐标三角形周长为16时,面积为. 22.(本题满分12分) 解:(1)∵ 30 000÷5 000=6, ∴ 能租出24间. (2)设每间商铺的年租金增加x万元,则 (30-)×(10+x)-(30-)×1-×0.5=275, 第23题图1 2 x 2-11x+5=0, ∴ x=5或0.5, ∴ 每间商铺的年租金定为10.5万元或15万元. 23.(本题满分12分) (1) 证明:如图1,∵ 四边形ABCD为正方形, ∴ AB=BC,∠ABC=∠BCD=90°, ∴ ∠EAB+∠AEB=90°. ∵ ∠EOB=∠AOF=90°, 第23题图2 O′ N M ∴ ∠FBC+∠AEB=90°,∴ ∠EAB=∠FBC, ∴ △ABE≌△BCF , ∴ BE=CF. (2) 解:如图2,过点A作AM//GH交BC于M, 过点B作BN//EF交CD于N,AM与BN交于点O/, 则四边形AMHG和四边形BNFE均为平行四边形, ∴ EF=BN,GH=AM, ∵ ∠FOH=90°, AM//GH,EF//BN, ∴ ∠NO/A=90°, 故由(1)得, △ABM≌△BCN, ∴ AM=BN, ∴ GH=EF=4. (3) ① 8.② 4n. 24.(本题满分14分) 解:(1)∵ 点A在抛物线C1上,∴ 把点A坐标代入得 =1. ∴ 抛物线C1的解析式为, 设B(-2,b), ∴ b=-4, ∴ B(-2,-4) . (2)①如图1, ∵ M(1, 5),D(1, 2), 且DH⊥x轴,∴ 点M在DH上,MH=5. 第24题图1 过点G作GE⊥DH,垂足为E, 由△DHG是正三角形,可得EG=, EH=1, ∴ ME=4. 设N ( x, 0 ), 则 NH=x-1, 由△MEG∽△MHN,得 , ∴ , ∴ , ∴ 点N的横坐标为. ② 当点D移到与点A重合时,如图2, 第24题图2 直线与DG交于点G,此时点N的横坐标最大. 过点G,M作x轴的垂线,垂足分别为点Q,F, 设N(x,0), ∵ A (2, 4), ∴ G (, 2), ∴ NQ=,NF =, GQ=2, MF =5. ∵ △NGQ∽△NMF, ∴ , ∴ , 第24题图3 图4 ∴ . 当点D移到与点B重合时,如图3, 直线与DG交于点D,即点B, 此时点N的横坐标最小. ∵ B(-2, -4), ∴ H(-2, 0), D(-2, -4), 设N(x,0), ∵ △BHN∽△MFN, ∴ , ∴ , ∴ . ∴ 点N横坐标的范围为 ≤x≤且x≠0. 查看更多