备战2020年高考数学大一轮复习 热点聚焦与扩展 专题31 数形结合之——简单线性规划

备战2020年高考数学大一轮复习 热点聚焦与扩展 专题31 数形结合之——简单线性规划

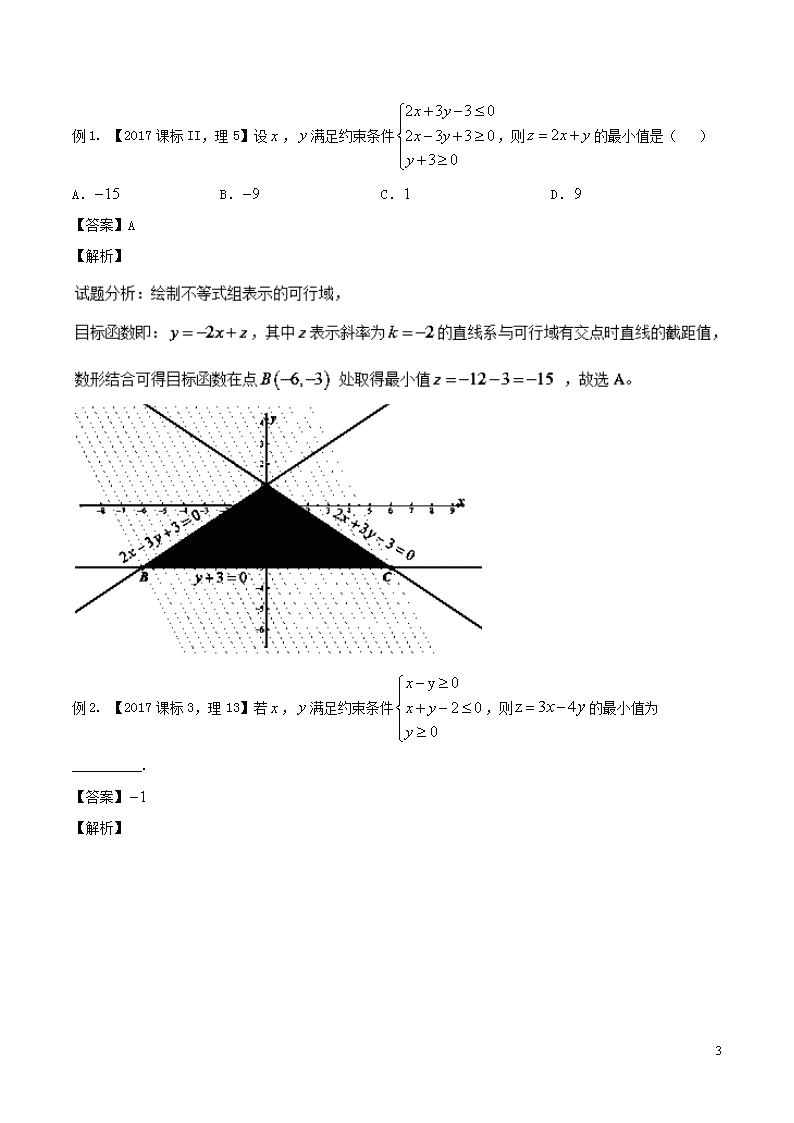
专题31 数形结合之----简单线性规划 ‎【热点聚焦与扩展】‎ ‎ 从考纲和考题中看，该部分内容难度不大，重点考查目标函数在线性约束条件下的最大值和最小值问题，或在目标函数的最值已知的条件下确定参数的值，命题形式以选择、填空为主，但也有解答题以应用题的形式出现．本专题重点说明利用数形结合法解答此类问题.‎ ‎（一）简单线性规划问题 ‎1、相关术语：‎ ‎（1）线性约束条件：关于变量的一次不等式（或方程）组 ‎（2）可行解：满足线性约束条件的解 ‎（3）可行域：所有可行解组成的集合 ‎（4）目标函数：关于的函数解析式 ‎（5）最优解：是目标函数取得最大值或最小值的可行解 ‎2、如何在直角坐标系中作出可行域：‎ ‎（1）先作出围成可行域的直线，利用“两点唯一确定一条直线”可选取直线上的两个特殊点（比如坐标轴上的点），以便快速做出直线 ‎（2）如何判断满足不等式的区域位于直线的哪一侧：一条曲线（或直线）将平面分成若干区域，则在同一区域的点，所满足不等式的不等号方向相同，所以可用特殊值法，利用特殊点判断其是否符合不等式，如果符合，则该特殊点所在区域均符合该不等式，具体来说有以下三种情况：‎ ‎① 竖直线或水平线：可通过点的横（纵）坐标直接进行判断 ‎② 一般直线：可代入点进行判断，若符合不等式，则原点所在区域即为不等式表示区域，否则则为另一半区域.例如：不等式，代入符合不等式，则所表示区域为直线的右下方 ‎③ 过原点的直线：无法代入，可代入坐标轴上的特殊点予以解决，或者利用象限进行判断.例如：：直线穿过一、三象限，二、四象限分居直线两侧.考虑第四象限的点，所以必有，所以第四象限所在区域含在表示的区域之中.‎ ‎（3）在作可行域时要注意边界是否能够取到：对于约束条件（或 20‎ ‎）边界不能取值时，在图像中边界用虚线表示；对于约束条件（或）边界能取值时，在图像中边界用实线表示 ‎3、利用数形结合寻求最优解的一般步骤 ‎（1）根据约束条件，在平面直角坐标系中作出可行域所代表的区域 ‎（2）确定目标函数在式子中的几何意义，常见的几何意义有：（设为常数）‎ ‎① 线性表达式——与纵截距相关：例如，则有，从而的取值与动直线的纵截距相关，要注意的符号，若，则的最大值与纵截距最大值相关；若，则的最大值与纵截距最小值相关.‎ ‎② 分式——与斜率相关（分式）：例如：可理解为是可行域中的点与定点连线的斜率.‎ ‎③ 含平方和——与距离相关：例如：可理解为是可行域中的点与定点距离的平方.‎ ‎（3）根据的意义寻找最优解，以及的范围（或最值）‎ ‎4、线性目标函数影响最优解选取的要素：当目标函数直线斜率与约束条件直线斜率符号相同时，目标函数直线斜率与约束条件直线斜率的大小会影响最优解的选取.‎ ‎（1）在斜率符号相同的情况下：越大，则直线越“陡”‎ ‎（2）在作图和平移直线的过程中，图像不必过于精确，但斜率符号相同的直线之间，陡峭程度要与斜率绝对值大小关系一致，这样才能保证最优解选取的准确 ‎（3）当目标函数的斜率与约束条件中的某条直线斜率相同时，有可能达到最值的最优解有无数多个（位于可行域的边界上）‎ ‎（4）当目标函数的斜率含参时，涉及到最优解选取的分类讨论，讨论通常以约束条件中同符号的斜率作为分界点.‎ ‎（二）非常规线性规划问题解答策略 第一依然要借助可行域及其图形；第二，要确定参数的作用，让含参数的图形运动起来寻找规律；第三，要能将图形中的特点与关系翻译成代数的语言，并进行精确计算.‎ ‎【经典例题】‎ 20‎ 例1. 【2017课标II，理5】设，满足约束条件，则的最小值是（ ）‎ A． B． C． D．‎ ‎【答案】A ‎【解析】‎ 例2. 【2017课标3，理13】若，满足约束条件，则的最小值为__________.‎ ‎【答案】 ‎ ‎【解析】‎ 20‎ ‎【名师点睛】求线性目标函数z＝ax＋by(ab≠0)的最值，当b＞0时，直线过可行域且在y轴上截距最大时，z值最大，在y轴截距最小时，z值最小；当b＜0时，直线过可行域且在y轴上截距最大时，z值最小，在y轴上截距最小时，z值最大.‎ 例3. 【2019年5月2019届高三第三次全国大联考】已知实数，满足约束条件，则的最小值为（ ）‎ A. B. C. D. ‎ ‎【答案】A ‎【解析】作出不等式组表示的平面区域如下图中阴影部分所示，易知表示可行域内的点到点的距离的平方，所以．故选A．‎ 20‎ 例4.【2019年5月2019届高三第三次全国大联考】已知实数满足约束条件，则的取值范围为（ ）‎ A. B. C. D. ‎ ‎【答案】B 例5.【2019届宁夏银川市第二中学二模】设不等式组所表示的平面区域是Ω1，平面区域Ω2与Ω1关于直线3x－4y－9＝0对称．对于Ω1中的任意点A与Ω2中的任意点B，|AB|的最小值等于(　　)‎ A. B. 4 C. D. 2‎ ‎【答案】B ‎【解析】分析：根据已知的约束条件，画出满足约束条件的可行域Ω1，根据对称的性质，不难得到：当A点距对称轴的距离最近时，|AB|有最小值．‎ 详解：‎ 20‎ 故选B.‎ 点睛：本题是常规的线性规划问题，线性规划问题常出现的形式有：①直线型，转化成斜截式比较截距，要注意前面的系数为负时，截距越大，值越小；②分式型，其几何意义是已知点与未知点的斜率；③平方型，其几何意义是距离，尤其要注意的是最终结果应该是距离的平方；④绝对值型，转化后其几何意义是点到直线的距离.‎ 例6.【2019届云南省曲靖市第一中学4月监测（七）】若不等式，表示的平面区域为三角形且其面积等于，则的最小值为（ ）‎ A. -2 B. C. -3 D. 1‎ ‎【答案】A ‎【解析】分析：先做出不等式组对应的平面区域，求出三角形的各顶点坐标，利用三角形的面积公式确定值，再利用平移目标函数直线确定最优解．‎ 详解：作出不等式组表示的平面区域（如图所示），‎ 20‎ 由图象，得当直线过点时，‎ 取得最小值为.故选A．‎ 例7．【2019届湖南师范大学附属中学高三月考六】已知满足约束条件若取得最大值的最优解不唯一，则实数的值为( )‎ A. 或-1 B. 2或 C. -2或1 D. 2或-1‎ ‎【答案】C ‎【解析】分析：作出不等式组对应的平面区域，利用目标函数的几何意义，得到直线的斜率的变换，从而求出的值.‎ 详解：作出不等式组表示的平面区域，如图所示，‎ 20‎ 则直线与直线平行，此时；‎ 综上或，故选C.‎ 例8.【2019届百校联盟TOP20四月联考】已知，若存在点，使得，则的取值范围为（ ）‎ A. B. C. D. ‎ ‎【答案】C ‎【解析】分析：作出不等式组表示的可行域，利用图象的直观性建立的不等式组，即可求出的取值范围.‎ 详解：作出不等式组表示的可行域，如图，‎ 要使可行域存在，必有，若可行域存在点，使得，‎ 则可行域内含有直线上的点，只需边界点在直线上方，‎ 20‎ 且在直线下方，解不等式，解得 故选：C 例9.【2019届山西省孝义市一模】已知不等式组表示的平面区域为，若函数的图象上存在区域上的点，则实数的取值范围是（ ）‎ A. B. C. D. ‎ ‎【答案】C 由可解得，即B（2，﹣1）此时有﹣1=|2﹣1|+m，解得m=﹣2；‎ 由可解得，即B（1，1）此时有1=|1﹣1|+m，解得m=1；‎ 故实数m的取值范围为[﹣2，1]，‎ 故答案为[﹣2，1]．‎ 故选C.‎ 20‎ 例10.【2019届北京市海淀区二模】两个居民小区的居委会欲组织本小区的中学生，利用双休日去市郊的敬老院参加献爱心活动.两个校区每位同学的往返车费及服务老人的人数如下表：‎ 小区 小区 往返车费 ‎3元 ‎5元 服务老人的人数 ‎5人 ‎3人 根据安排，去敬老院的往返总车费不能超过37元，且小区参加献爱心活动的同学比小区的同学至少多1人，则接受服务的老人最多有____人.‎ ‎【答案】‎ ‎【解析】分析：设两区参加活动同学的人数分别为，受到服务的老人人数为，‎ 找出约束条件与目标函数，准确地描画可行域,平移直线可求得满足题设的最优解.‎ 详解：‎ 当时，取得最大值为，‎ 即接受服务的老人最多有人，故答案为.‎ ‎【精选精练】‎ 20‎ ‎1.【2019届辽宁省丹东市模拟二】若点满足不等式组，则的取值范围为（ ）‎ A. B. ‎ C. D. ‎ ‎【答案】A ‎【解析】分析：将不等式组的可行域表示在平面直角坐标系中，进而利用，即，转化为区域内的点和定点连线的斜率即可.‎ 详解：‎ 故选A.‎ ‎2.【2019届黑龙江省哈尔滨师范大学附属中学三模】设点满足约束条件,且,则这样的点共有( ）个 A. 12 B. 11 C. 10 D. 9‎ 20‎ ‎【答案】A ‎【解析】分析：由约束条件画出可行域，根据可行域，利用,可逐一写出满足条件的点，从而可得结果.‎ 详解：‎ 画出表示的可行域，由图可知，满足，得，‎ 共有，，‎ 共个，故选A.‎ ‎3.【2019届陕西省咸阳市三模】已知实数，满足给，中间插入5个数，这7个数构成以为首项，为末项的等差数列，则这7个数和的最大值为（ ）‎ A. B. C. D. ‎ ‎【答案】D ‎【解析】分析：实数x，y满足，如图所示，画出可行域△ABC．给x，y中间插入5个数，这7个数构成以x为首项，y为末项的等差数列，则这7个数和=，令x+y=t，则y=﹣x+t．利用线性规划 20‎ 因此这7个数和=的最大值为，‎ 故答案为：D ‎4．【2019届相阳教育“黉门云”高考模拟】已知,满足约束条件，若的最小值为1，则=（ ）‎ A. 2 B. 1 C. D. ‎ ‎【答案】C ‎【解析】画出可行域如下图所示,由图可知,目标函数在点处取得最小值,即.故选C.‎ 20‎ ‎5．【2019届第三次全国大联考】已知不等式组表示的平面区域为，若以原点为圆心的圆与无公共点，则圆的半径的取值范围为（ ）‎ A. B. C. D. ‎ ‎【答案】D ‎【解析】作出不等式组表示的平面区域，如图中阴影部分所示，‎ 可知当圆的半径小于原点到直线的距离或大于时，圆与无公共点，而原点到直线的距离为，，故圆的半径的取值范围为.‎ ‎6．【2019届浙江省宁波市5月模拟】已知实数，满足不等式组，则的最大值为（ ）‎ 20‎ A. 0 B. 2 C. 4 D. 8‎ ‎【答案】C ‎|x﹣y|的几何意义：表示区域内的点到直线x﹣y=0的距离的倍，‎ 由图可知点A(4,0)到直线x-y=0距离最大，所以|x﹣y|的最大值为 故答案为：C．‎ 点睛：本题解题的关键是发现|x-y|的几何意义，|x-y|它表示区域内的点到直线x﹣y=0的距离的倍，利用数形结合分析解答，可以提高解题效率.所以在今后的解题过程中，看到|ax+by|要联想到点到直线的距离公式.‎ ‎7．【2019届广东省佛山市检测二】已知，设满足约束条件，且的最小值为-4，则 ( )‎ A. 1 B. 2 C. 3 D. 4‎ ‎【答案】C 20‎ 故选C.‎ ‎8.【2019届安徽省“皖南八校”第三次（4月）联考】已知函数，若满足，则的取值范围是（ ）‎ A. B. C. D. ‎ ‎【答案】C ‎【解析】分析：由已知条件可得，函数是定义在上的奇函数，从而将题中的条件转化为关于的二元一次不等式组，画出相应的可行域，之后结合目标函数的几何意义，确定最优解的位置，从而求得范围.‎ 20‎ 最小值，在点处取得最大值，而边界值取不到，故答案是，故选C.‎ ‎9.【2019届高考全程训练】某研究所计划利用“神舟十一号”飞船进行新产品搭载实验，计划搭载新产品，要根据该产品的研制成本、产品质量、搭载实验费用和预计产生收益来决定具体安排，通过调查，搭载每件产品有关数据如表：‎ 因素 产品 产品 备注 研制成本、搭载费用之和/万元 ‎ ‎20‎ ‎30‎ 计划最大投资 金额300万元产品质量/千克 ‎10‎ ‎5‎ 最大搭载 质量110千克预计收益/万元 ‎80‎ ‎60‎ ‎——‎ 则使总预计收益达到最大时， 两种产品的搭载件数分别为(　　)‎ A. 9,4 B. 8,5 C. 9,5 D. 8,4‎ ‎【答案】A 由解得,故M(9,4)．‎ 20‎ 所以目标函数的最大值为zmax＝80×9＋60×4＝960，此时搭载产品A有9件，产品B有4件．‎ 故选A.‎ ‎10.【2019届第二次全国大联考】若满足不等式组，则目标函数的取值范围是_____．‎ ‎【答案】 ‎ ‎【解析】 ，‎ 令，并作出不等式组表示的可行域如图中阴影部分所示，‎ ‎11．【2019届辽宁省丹东市测试二】设实数，满足约束条件，则的取值范围为_______．‎ ‎【答案】‎ ‎【解析】分析：画出不等式组表示的可行域，将变形为，然后平移直线确定取最小和最大值时的最优解，进而可得所求范围．‎ 详解：画出不等式组表示的可行域（如图阴影部分所示）．‎ 20‎ ‎12．【2019届江西省景德镇市第一中学等盟校第二次联考】若实数，满足，则的取值范围是__________．‎ ‎【答案】‎ ‎【解析】分析：画出可行域，设,化为，平移直线，由可行域可得的取值范围，从而可得的取值范围.‎ 详解：‎ 设,化为，‎ 画出，表示的可行域，平移直线，如图，‎ 20‎ 故答案为.‎ 20‎