八年级下册数学同步练习第三章复习 北师大版

八年级下册数学同步练习第三章复习 北师大版

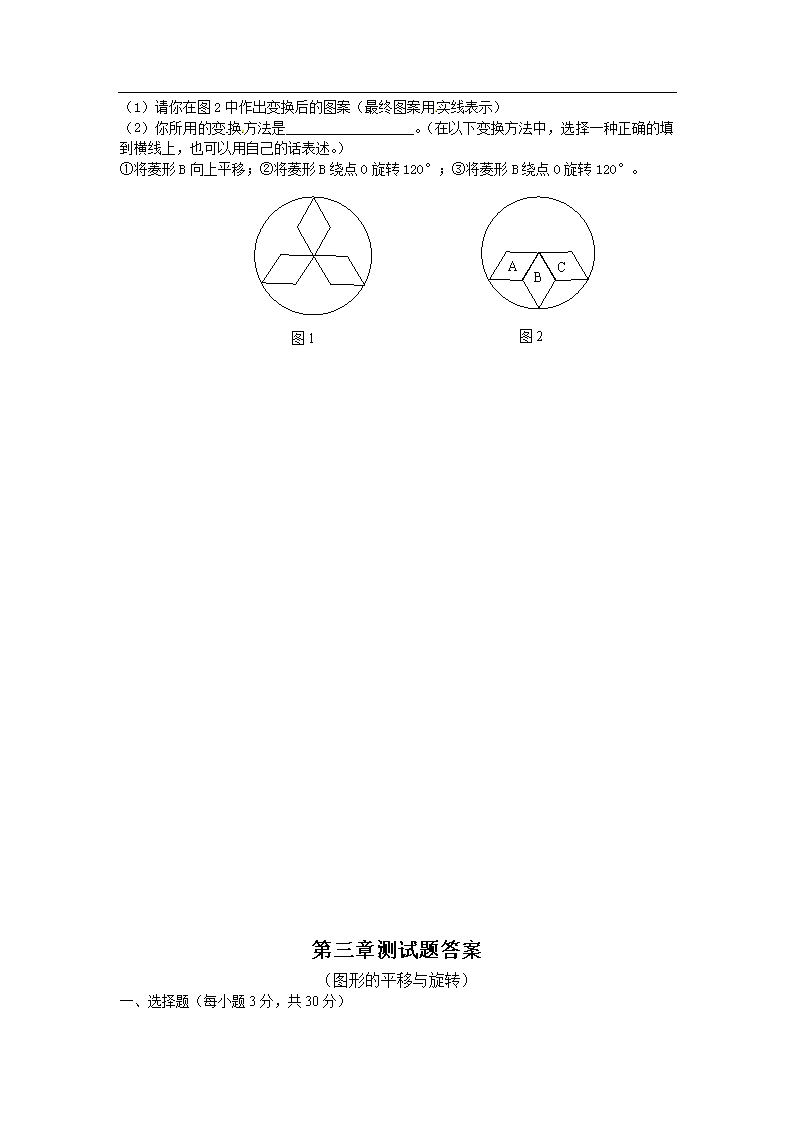
第三章复习 一、选择题（每小题3分，共30分）‎ ‎1、下列图形经过平移后恰好可以与原图形组合成一个长方形的是（ ）‎ A、三角形 B、正方形 C、梯形 D、都有可能 ‎2、在图形平移的过程中，下列说法中错误的是（ ）‎ A、图形上任意点移动的方向相同 B、图形上任意点移动的距离相同 C、图形上可能存在不动的点 D、图形上任意两点连线的长度不变 ‎3、有关图形旋转的说法中错误的是（ ）‎ A、图形上每一点到旋转中心的距离相等 B、图形上每一点移动的角度相同 C、图形上可能存在不动点 D、图形上任意两点连线的长度与旋转其对应两点连线的长度相等。‎ ‎4、如右图所示，观察图形，下列结论正确的是（ ）‎ A、它是轴对称图形，但不是旋转对称图形；‎ B、它是轴对称图形，又是旋转对称图形；‎ C、它是旋转对称图形，但不是轴对称图形；‎ D、它既不是旋转对称图形，又不是轴对称图形。‎ ‎5、下列图形中，既是轴对称图形，又是旋转对称图形的是（ ）‎ A、等腰三角形 B、平行四边形 C、等边三角形 D、三角形 ‎6、等边三角形的旋转中心是什么？旋转多少度能与原来的图形重合（ ）‎ A、三条中线的交点，60° B、三条高线的交点，120°‎ C、三条角平分线的交点，60° D、三条中线的交点，180°‎ ‎7、如图1，△BOD的位置经过怎样的运动和△AOC重合（ ）‎ A B C D O 图3‎ A、翻折 B、平移 C、旋转90° D、旋转180°‎ A B C D E 图2‎ 图1‎ A C D B O ‎[来源:Z+xx+k.Com][来源:学科网ZXXK]‎ ‎8、钟表上12时15分钟时，时针与分针的夹角为（ ）‎ ‎ A、90° B、82.5° C、67.5° D、60°‎ 二、填空题（每小题4分，共32分）‎ ‎9、经过平移， 和 平行且相等， 相等。‎ ‎10、如图2，△ABC中，∠ACB=90°，AB=13,AC=12,将△ABC沿射线BC的方向平移一段距离后得到△DCE，那么CD= ；BD= 。‎ ‎11、如图3所示，∠AOB=∠COB=60°,OA=OB,OC=OD,把△AOC绕点O顺时针旋转60°，点A将与点 重合，点C将与点 重合，因此△AOC与△BOD可以通过 得到。‎ ‎12、正方形至少旋转 能与自身重合，正六边形至少旋转 ‎ 能与自身重合。‎ ‎13、如图4，等边三角形ABC旋转后能与等边三角形DBC重合，那么在图形所在的平面上可以作为旋转中心的点共有 个。‎ A B C D O 图5‎ A B C D 图4‎ ‎14、如图5，△ABC≌△CDA,BD交AC于点O，则△ABC绕点O旋转 后与△CDA重合，△ABO可以由△CDO绕点 旋转 得到。‎ 三、解答题（58分）‎ ‎15、（10分）如右图所示，△ABC是直角三角形，BC是斜边，将△ABP绕点A逆时针旋转后，‎ 能与△ACP′重合，如果AP=3，求PP′的长。‎ A B C P′‎ P ‎16、（10分）如图所示，在等腰直角三角形ABC中，AD为斜边上的高，点E、F分别在AB、AC上，△AED经过旋转到了△CDF的位置。‎ ‎⑴ △BED和△AFD之间可以看成是经过怎样的变换得到的？‎ ⑵ AD与EF相交于点G，试判断∠AED与∠AGF的大小关系，并说明理由。‎ A B D C F E G ‎[来源:学&科&网]‎ ‎17、（10分）某产品的标志图案如图1所示，要在所给的图形图2中，把A、B、C三个菱形通过一种或几种变换，使之变为与图1一样的图案。‎ ‎（1）请你在图2中作出变换后的图案（最终图案用实线表示）‎ ‎（2）你所用的变换方法是 。（在以下变换方法中，选择一种正确的填到横线上，也可以用自己的话表述。）‎ ‎①将菱形B向上平移；②将菱形B绕点O旋转120°；③将菱形B绕点O旋转120°。‎ 图2‎ C A B 图1‎ ‎ ‎ ‎[来源:学*科*网Z*X*X*K]‎ 第三章测试题答案 ‎（图形的平移与旋转）‎ 一、选择题（每小题3分，共30分）‎ ‎1、B 2、D 3、B 4、C 5、A 6、B 7、C 8、B 9、D 10、B 二、填空题（每小题4分，共32分）‎ ‎11、对应点所连的线段和对应线段；对应角。 12、13；。 13、以大五角星的中心。 14、平移，旋转，轴对称。 15、B；D；相互旋转。 16、90°；60°。 17、三。 18、180°；O；180°。‎ 三、解答题（58分）‎ ‎19、解：（1）点A的对应点是点D ；‎ ‎（2）AD=3㎝；[来源:学科网ZXXK]‎ ‎（3）∠ABC=∠DEF；‎ ‎（4）从图形发现了：①对应线段、对应角相等；②对应点所连的线段平行（或在同一直线）且相等。‎ A B C M N D E F ‎20、解：作图如下：‎ ‎ 所以△DEF就是△ABC平移后的图形。‎ ‎21、解：∵△ABP绕点A逆时针旋转后与△ACP′重合，‎ A B C P′‎ P ‎∴AP′= AP=3,∠BAP=∠CAP′,‎ ‎∴∠PAP′=∠PAC+∠CAP′=∠PAC+∠BAP=∠BAC=90°,‎ ‎∴PP′===.‎ ‎22、解：⑴△BED绕点D顺时针旋转90°得到的△AFD；‎ ‎△AFD绕点D逆时针旋转90°得到的△BED。‎ ‎（2）∵△AED经过旋转到了△CDF的位置，∴∠ADE=∠CDF,DE=DF,‎ A B D C F E G ‎∵∠EDF=∠ADE+∠ADF, ∴∠EDF=∠CDF+∠ADF,‎ ‎ ∵AD为斜边上的高，∴∠ADC=90°, ∴∠EDF=90°,‎ ‎ ∴△EFD是等腰直角三角形，∴∠ DFE=45°, ‎ ‎∴∠AGF=∠ADF+∠ DFE=∠ADF+45°,‎ ‎∵∠CFD=∠ADF+∠DAF=∠ADF+45°,‎ ‎∴∠AGF=∠CFD, ∵∠AED=∠CFD,‎ ‎∴∠AED=∠AGF.‎ 图2‎ A CC BC ‎23、解：（1）变换后的图案如右图所示：‎ ‎ （2）你所用的变换方法是：①将菱形B向上平移 。‎ ‎24、解：（1）过点O分别作OP⊥AB于P,OQ⊥AD于Q。‎ ‎ 则∠OPM=∠OQN=90°,OP=OQ,‎ ‎ ∵∠POM+∠MOQ=∠QON+∠MOQ=90°,‎ ‎ ∴∠POM=∠QON,‎ ‎ ∴△POM≌△QON,‎ ‎ ∴‎ A B C D F E G O Q P M N ‎ =㎝。‎ ‎ （2）如果正方形OGEF的边长是4㎝，则 ‎ ‎ ‎ =㎝。‎ ‎ 所以阴影部分的面积不变，仍为㎝。‎ ‎ （3）如果正方形OGEF的边长是5㎝或6㎝，则 ‎ ‎ ‎ =㎝。‎ ‎ 所以阴影部分的面积不变，仍为㎝。‎ ‎ （4）由此可以发现：若正方形ABCD的边长是3㎝不变，改变正方形OGEF的边长，但两个正方形重叠的阴影部分的面积仍为㎝。‎