2017年4月福建省高三数学（文科）有详细答案

2017年4月福建省高三数学（文科）有详细答案

‎2017年4月福建省高三数学（文科）质量检测试题 一、 选择题：( 共12题每小题5分)‎ ‎1、已知集合U=‎-1，0，1‎ ，A=xx=m‎2‎,m∈U ,则CUA=‎（ ）‎ A、{0,1} B{-1,0,1} C、 ∅ D、{-1}‎ ‎2、已知正方形ABCD边长为1，向量AB=a ,‎ ‎BC=b ,‎ ‎CD=c则a+b+c‎=‎( )‎ A、1 B、‎2‎ C、‎2‎‎2‎ D、 3‎ ‎3、某网店出售一种饼干，有草莓味，巧克力味、香蕉味，香芋味共四种口味。一个顾客在该店购买了两袋这种饼干，口味选择，随机派送。则这位顾客买到的饼干是同一种口味的概率为（ ）‎ A、‎1‎‎16‎ B、‎1‎‎4‎ C、‎2‎‎5‎ D、‎‎2‎‎3‎ ‎4、若x,y满足约束条件x-y≥0‎x+2y-3≥0‎‎2x+y-6≤0‎ 则Z=x-2y的最小值为（ ）‎ A、-6 B-2 C、-1 D、3‎ ‎5、△ABC中，角A，B，C，所对的边分别为a,b,c,若a=‎6‎‎2‎b,A =2B则CosB=（ ）‎ A、‎6‎‎6‎ B、‎6‎‎5‎ C、‎6‎‎4‎ D、‎‎6‎‎3‎ ‎6、已知递增的等比数列{an}的公比为q,其前n项和Sn＜0，则（ ）‎ A、a1<0,01 C、a1>0, 00，q>1‎ ‎7、右图是某几何体的三视图，正视图、侧视图、俯视图 都是边长为2正方形.则该几何体的体积为（ ）‎ A、8-‎4‎‎3‎π B、8-π C、8-‎2‎‎3‎π D、8-‎‎1‎‎3‎π ‎8、函数y=x‎3‎+ln(x‎2‎‎+1‎‎-x)‎的图像大致为（ ）‎ 开始 输入a 输出b i=1‎ a=1-‎‎1‎a i=i+1‎ b=2a i‎≤2017?‎ 结束 ‎9、执行如图所示的程序框图，若输入的a的 值为2，则输出的b的值为（ ）‎ A-2 B 1 C 2 D 4‎ ‎10、已知函数f(x)=‎3‎sin2x+2cos‎2‎x 下列结论正确的是（ ）‎ A、函数f(x)的最小正周期为2π； B、函数f(x)在（π‎12‎‎，‎π‎4‎）上是增函数 C、函数f(x)的图像关于x=‎π‎6‎ 对称 D、函数f(x)的图像关于（ ‎-‎π‎12‎,0）对称 ‎11、已知正三棱柱ABC-A1B1C1的顶点A1，B1，C1在同一个球面上，且平面ABC经过球心。若此球的表面积为4π，则此三棱柱的侧面积最大值为（ ）‎ A、‎3‎‎3‎ B、‎3‎ C、‎3‎‎3‎‎3‎ D、‎‎3‎‎3‎ ‎12、设F是椭圆C：x‎2‎a‎2‎‎+‎y‎2‎b‎2‎=1（a>b>0）的焦点，P是C上的点。圆x‎2‎‎+‎y‎2‎=‎a‎2‎‎9‎ 与线段PF交与A，B两点，若A，B三等分PF，则C的离心率为（ ）‎ A、‎3‎‎3‎ B、‎5‎‎3‎ C、‎10‎‎4‎ D、‎‎17‎‎5‎ 二、填空题：（共四小题，每小题5分）‎ ‎13、已知复数Z=‎1+3i‎2+i ,则Z= ‎ ‎14、已知α是第一象限角，sin(π-α)=‎3‎‎5‎，则tanα= ‎ ‎15、过双曲线：x‎2‎-y‎2‎=1的焦点且垂直x轴的直线交双曲线于A，B两点.‎ 则AB‎=‎ ‎ ‎16、函数f(x)=alnx+x2+（a-6）x在（0，3）上不是单调函数。则实数a的取值范围是 ‎ ‎ ‎ 解答题：（共六题）‎ ‎17、（本小题满分12分）已知等差数列{an}的前n项和Sn,a2=2,S5=15,‎ 数列{bn}的前n项和Tn=（n+5）an ‎(1)求an；（2）求{‎1‎anbn}的前n项和。‎ ‎18、（本小题满分12分）某通信商推出两款套餐，详情如下：‎ 套餐名称 月套餐费（单位：元）‎ 月套餐流量（单位：M）‎ A ‎20‎ ‎300‎ B ‎30‎ ‎500‎ 这两款套餐都有如下的附加条款：套餐费月初一次性收取；手机流量一旦超出套餐流量，系统就自动帮助用户充值200M流量，充值费20元；如果再次超出套餐流量，系统就再次自动帮助用户充值200M流量，充值费20元/次；以此类推。如果当月流量有剩余，系统将自动清零，无法转入下月使用。‎ 小王过去50个月手机月使用的流量（单位：M）的频数分布表如下：‎ 月使用流量分组 ‎[100,200]‎ ‎(200,300]‎ ‎(300,400]‎ ‎(400,500]‎ ‎(500,600]‎ ‎(600,700]‎ 频数 ‎4‎ ‎11‎ ‎12‎ ‎18‎ ‎4‎ ‎1‎ 根据小王过去50个月手机月使用的流量情况，回答以下问题：‎ ‎（1）若小王订购A套餐，假设小王月实际使用流量为x，‎ ‎（单位：M,100‎‎≤x≤700)‎ 月使用流量费用为y(单位：元)将y表示成x的函数；‎ ‎（2）小王拟定在A套餐或B套餐中选定一款，若以月平均使用费用为决策依据，他应选购那一款？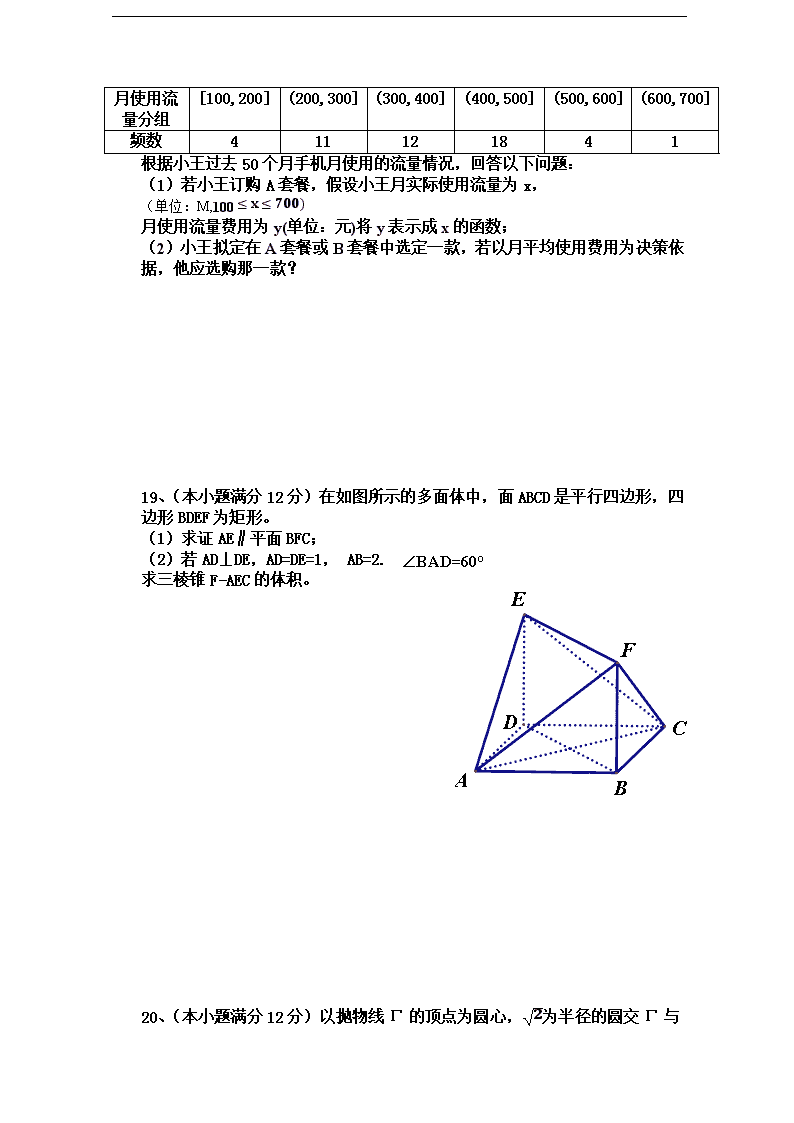‎ ‎19、（本小题满分12分）在如图所示的多面体中，面ABCD是平行四边形，四边形BDEF为矩形。‎ ‎（1）求证AE∥平面BFC；‎ ‎（2）若AD⊥DE，AD=DE=1， AB=2.‎ 求三棱锥F-AEC的体积。‎ ‎20、（本小题满分12分）以抛物线Г的顶点为圆心，‎2‎为半径的圆交Г 与A，B两点，且AB=2‎ ‎（1）建立适当的坐标系，求Г的方程；（2）若过点A且与Г只有一个公共点的直线l交Г的对称轴于点C，点D在线段AB上。直线CD与Г交于P，Q两点。求证：PC‎∙‎QD=PD‎∙‎QC ‎21、（本小题满分12分）已知函数f(x)=‎℮‎‎-x‎+ax, a∈R ‎ ‎（1）讨论f(x)的最值 ‎（2）若a=0,求证：f(x)‎‎>-‎1‎‎2‎x‎2‎+‎‎5‎‎8‎ ‎ ‎ ‎22、（本小题满分10分）坐标系与参数方程 在平面直角坐标系x0y中，曲线C1的参数方程为x=2+2cost‎2sint (t为参数)‎ 在以坐标原点为极点，x轴正半轴为极轴的极坐标系中，曲线C2：ρ=2sinθ,曲线C3：‎ Θ=‎π‎6‎‎ （ρ>0）,A(2,0)‎ ‎(1)把C1的参数方程化成极坐标方程；（2）设C3分别与C1，C2交于P,Q两点，求△APQ的面积。‎ ‎23、（本小题满分10分）不等式选讲：‎ 已知函数f(x)=‎2x+1‎+x-2‎,集合A={xf(x)<3‎} ‎ (1) 求A；（2）S，t∈A，求证：‎‎1-‎ts‎<‎t-‎‎1‎s