- 2021-04-15 发布 |
- 37.5 KB |
- 9页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
高考文科立体几何考试大题题型
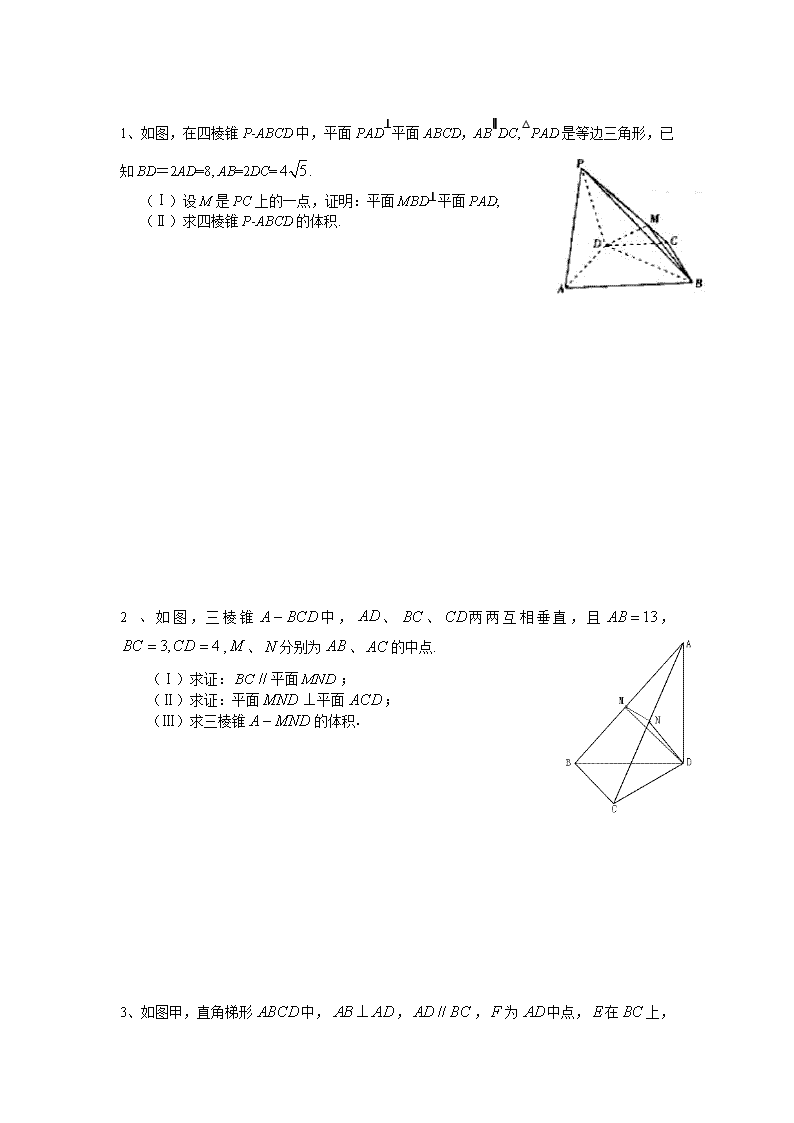
高考文科数学立体几何大题题型 基本平行、垂直 1、如图,在四棱台中,平面,底面是平行四边形,,,60°. (Ⅰ)证明:; (Ⅱ)证明:. 2.如图,四棱锥中,四边形为矩形,为等腰三角形,,平面 平面,且.分别为和的中点. (1)证明:平面; (2)证明:平面平面; (3)求四棱锥的体积. 3. 如图,已知四棱锥中,底面是直角梯形,, ,, ,平面,. A B C D P M (1)求证:平面;[来源:Z.xx.k.Com] (2)求证:平面; (3)若M是PC的中点,求三棱锥M—ACD的体积. ks5u ks5u ks5u ks5u ks5u ks5u ks5u ks5u ks5u ks5u ks5u ks5u ks5u ks5u ks5u ks5u ks5u ks5u ks5u ks5u ks5u ks5u ks5u ks5u ks5u ks5u ks5u ks5u ks5u ks5u ks5u ks5u ks5u ks5u ks5u ks5u ks5u ks5u ks5u ks5u ks5u ks5u ks5u ks5u ks5u ks5u ks5u ks5u ks5u ks5u ks5u ks5u ks5u ks5u ks5u ks5u ks5u ks5u ks5u ks5u ks5u ks5u ks5u ks5u ks5u 4.如图,四棱锥中,平面,四边形是矩形,、分别是、的中点.若,. (Ⅰ)求证:平面; (Ⅱ) 求点到平面的距离; 体积: 1、如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,AB∥DC,△PAD是等边三角形,已知BD=2AD=8, AB=2DC=. (Ⅰ)设M是PC上的一点,证明:平面MBD⊥平面PAD; (Ⅱ)求四棱锥P-ABCD的体积. 2、如图,三棱锥中,、、两两互相垂直,且,,、分别为、的中点. (Ⅰ)求证:平面; (Ⅱ)求证:平面平面; (Ⅲ)求三棱锥的体积. 3、如图甲,直角梯形中,,,为中点,在 上,且,已知,现沿把四边形折起如图乙,使平面⊥平面. ()求证: (Ⅱ)求证:平面; (Ⅲ求三棱锥的体积。 立体几何中的三视图问题 1.已知某几何体的直观图与它的三视图,其中俯视图为正三角形,其它两个视图是矩形.已知是这个几何体的棱上的中点。 (1)求出该几何体的体积; (2)求证:直线; (3)求证:平面. C A B C1 A1 B1 D _ 3 _ 3 _ 1 _ 2 _ 1 _ 1 _ 2 _ 1 主视图 侧视图 俯视图 2. 已知四棱锥的三视图如下图所示,其中主视图、侧 视图是直角三角形,俯视图是有一条对角线的正方形.是侧棱 上的动点. (1)求证: (2)若五点在同一球面上,求该球的体积. A B C D P E 主视图 1 左视图 2 俯视图视图 3.一个三棱柱直观图和三视图如图所示, 设、分别为和的中点. (Ⅰ)求几何体的体积; (Ⅱ)证明:平面; (Ⅲ)证明:平面平面. 立体几何中的动点问题 1.已知四边形为矩形,、分别是线段、的中点,平面 (1)求证:; (2)设点在上,且平面,试确定点的位置. P A B E F C D · 2.如图,己知中,,, 且 (1)求证:不论为何值,总有 (2)若求三棱锥的体积. 3.如图,已知△ABC内接于圆O,AB是圆O的直径,四边形DCBE 为平行四边形,DC平面ABC ,, . (1)证明:平面ACD平面; (2)记,表示三棱锥A-CBE的体积,求的表达式; (3)当取得最大值时,求证:AD=CE. 立体几何中的翻折问题ks5u ks5u ks5u ks5u ks5u ks5u ks5u ks5u ks5u ks5u ks5u ks5u ks5u ks5u ks5u ks5u ks5u ks5u ks5u ks5u ks5u ks5u ks5u ks5u ks5u ks5u ks5u ks5u ks5u ks5u 1. 如图1,在直角梯形中,,,.将沿折起,使平面平面,得到几何体,如图2所示. A B C D 图2 (Ⅰ) 求证:平面; B A C D 图1 (Ⅱ) 求几何体的体积. 图6 2. 如图6,在直角梯形ABCP中,AP//BC,APAB,AB=BC=, D是AP的中点,E,F,G分别为PC、PD、CB的中点,将沿 CD折起,使得平面ABCD,如图7. (Ⅰ)求证:AP//平面EFG; 图7 (Ⅲ)求三棱椎的体积.查看更多