2020九年级数学下册 中考模拟卷 （新版）新人教版

2020九年级数学下册 中考模拟卷 （新版）新人教版

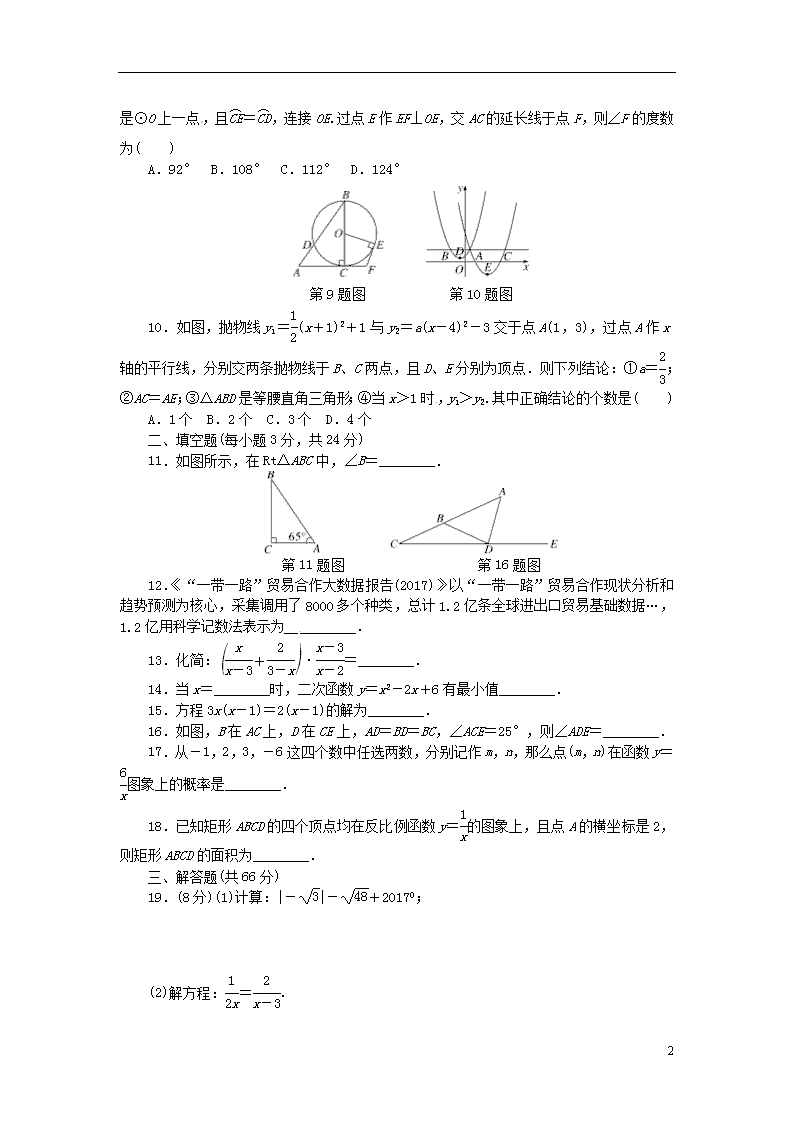
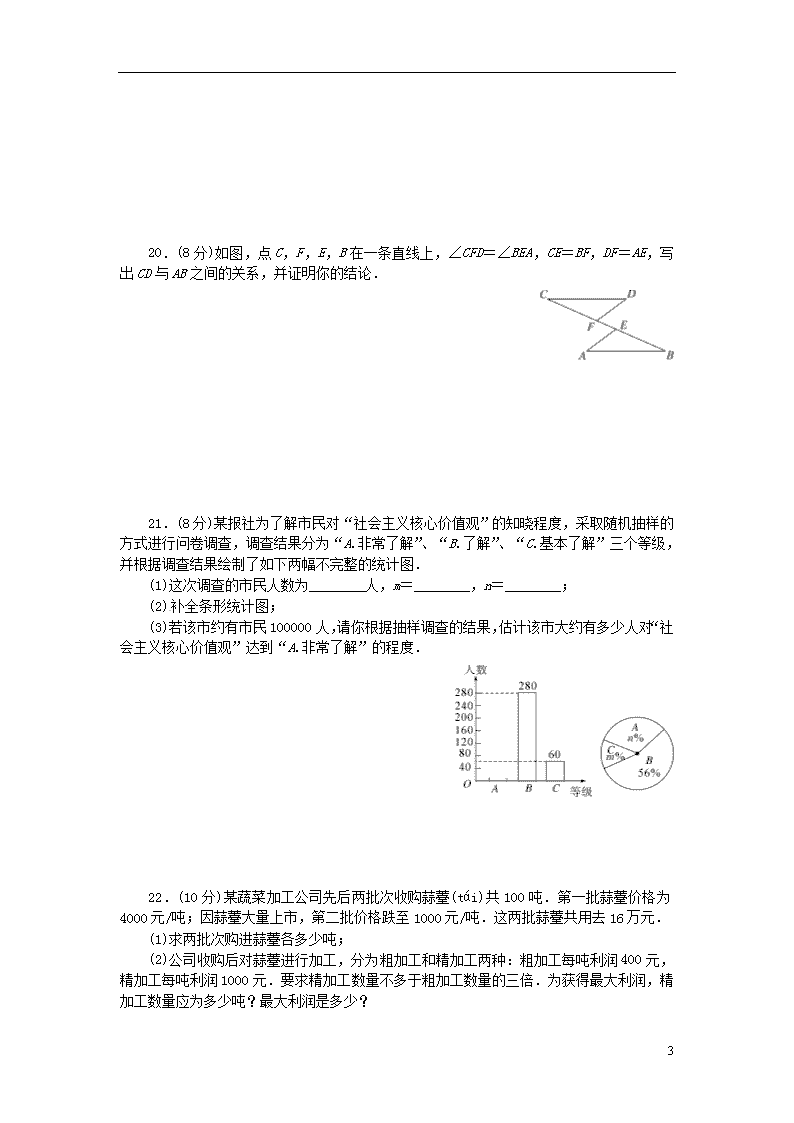
‎2018年中考模拟卷 时间：120分钟　　　　　满分：120分 题号 一 二 三 总分 得分 一、选择题(每小题3分，共30分)‎ ‎1．《九章算术》中注有“今两算得失相反，要令正负以名之”，意思是：今有两数若其意义相反，则分别叫作正数与负数．若气温为零上‎10℃‎记作＋‎10℃‎，则－‎3℃‎表示气温为(　　)‎ A．零上‎3℃‎ B．零下‎3℃‎ C．零上‎7℃‎ D．零下‎7℃‎ ‎2．不等式4－2x＞0的解集在数轴上表示为(　　)‎ ‎3．下列运算正确的是(　　)‎ A．‎3m－‎2m＝1 B．(m3)2＝m6‎ C．(－‎2m)3＝－‎2m3‎ D．m2＋m2＝m4‎ ‎4．如图所示的几何体的俯视图为(　　)‎ ‎5．某校举行“汉字听写比赛”，5个班级代表队的正确答题数如图．这5个正确答题数所组成的一组数据的中位数和众数分别是(　　)‎ A．10，15 B．13，‎15 C．13，20 D．15，15‎ ‎ ‎ 第5题图 第6题图 ‎6．如图，在▱ABCD中，连接AC，∠ABC＝∠CAD＝45°，AB＝2，则BC的长是(　　)‎ A. B．‎2 C．2 D．4‎ ‎7．若△ABC的每条边长增加各自的10%得△A′B′C′，则∠B′的度数与其对应角∠B的度数相比(　　)‎ A．增加了10% B．减少了10%‎ C．增加了(1＋10%) D．没有改变 ‎8．如果点A(x1，y1)和点B(x2，y2)是直线y＝kx－b上的两点，且当x1＜x2时，y1＜y2，那么函数y＝的图象位于(　　)‎ A．一、四象限 B．二、四象限 ‎ C．三、四象限 D．一、三象限 ‎9．如图，在Rt△ABC中，∠ACB＝90°，∠A＝56°.以BC为直径的⊙O交AB于点D.E 8‎ 是⊙O上一点，且＝，连接OE.过点E作EF⊥OE，交AC的延长线于点F，则∠F的度数为(　　)‎ A．92° B．108° C．112° D．124°‎ ‎ ‎ 第9题图 第10题图 ‎10．如图，抛物线y1＝(x＋1)2＋1与y2＝a(x－4)2－3交于点A(1，3)，过点A作x轴的平行线，分别交两条抛物线于B、C两点，且D、E分别为顶点．则下列结论：①a＝；②AC＝AE；③△ABD是等腰直角三角形；④当x＞1时，y1＞y2.其中正确结论的个数是(　　)‎ A．1个 B．2个 C．3个 D．4个 二、填空题(每小题3分，共24分)‎ ‎11．如图所示，在Rt△ABC中，∠B＝________．‎ ‎ ‎ 第11题图 第16题图 ‎12．《“一带一路”贸易合作大数据报告(2017)》以“一带一路”贸易合作现状分析和趋势预测为核心，采集调用了8000多个种类，总计1.2亿条全球进出口贸易基础数据…，1.2亿用科学记数法表示为__________．‎ ‎13．化简：·＝________．‎ ‎14．当x＝________时，二次函数y＝x2－2x＋6有最小值________．‎ ‎15．方程3x(x－1)＝2(x－1)的解为________．‎ ‎16．如图，B在AC上，D在CE上，AD＝BD＝BC，∠ACE＝25°，则∠ADE＝________．‎ ‎17．从－1，2，3，－6这四个数中任选两数，分别记作m，n，那么点(m，n)在函数y＝图象上的概率是________．‎ ‎18．已知矩形ABCD的四个顶点均在反比例函数y＝的图象上，且点A的横坐标是2，则矩形ABCD的面积为________．‎ 三、解答题(共66分)‎ ‎19．(8分)(1)计算：|－|－＋20170；‎ ‎(2)解方程：＝.‎ 8‎ ‎20．(8分)如图，点C，F，E，B在一条直线上，∠CFD＝∠BEA，CE＝BF，DF＝AE，写出CD与AB之间的关系，并证明你的结论．‎ ‎21．(8分)某报社为了解市民对“社会主义核心价值观”的知晓程度，采取随机抽样的方式进行问卷调查，调查结果分为“A.非常了解”、“B.了解”、“C.基本了解”三个等级，并根据调查结果绘制了如下两幅不完整的统计图．‎ ‎(1)这次调查的市民人数为________人，m＝________，n＝________；‎ ‎(2)补全条形统计图；‎ ‎(3)若该市约有市民100000人，请你根据抽样调查的结果，估计该市大约有多少人对“社会主义核心价值观”达到“A.非常了解”的程度．‎ ‎22．(10分)某蔬菜加工公司先后两批次收购蒜薹(tái)共100吨．第一批蒜薹价格为4000元/吨；因蒜薹大量上市，第二批价格跌至1000元/吨．这两批蒜薹共用去16万元．‎ ‎(1)求两批次购进蒜薹各多少吨；‎ ‎(2)公司收购后对蒜薹进行加工，分为粗加工和精加工两种：粗加工每吨利润400元，精加工每吨利润1000元．要求精加工数量不多于粗加工数量的三倍．为获得最大利润，精加工数量应为多少吨？最大利润是多少？‎ 8‎ ‎23．(10分)如图，在四边形ABCD中，AD＝BC，∠B＝∠D，AD不平行于BC，过点C作CE∥AD交△ABC的外接圆O于点E，连接AE.‎ ‎(1)求证：四边形AECD为平行四边形；‎ ‎(2)连接CO，求证：CO平分∠BCE.‎ ‎24．(10分)如图是小强洗漱时的侧面示意图，洗漱台(矩形ABCD)靠墙摆放，高AD＝‎80cm，宽AB＝‎48cm，小强身高‎166cm，下半身FG＝‎100cm，洗漱时下半身与地面成80°(∠FGK＝80°)，身体前倾成125°(∠EFG＝125°)，脚与洗漱台距离GC＝‎15cm(点D，C，G，K在同一直线上)．‎ ‎(1)此时小强头部E点与地面DK相距多少？‎ ‎(2)小强希望他的头部E恰好在洗漱盆AB的中点O的正上方，他应向前或后退多少？‎ ‎(sin80°≈0.98，cos80°≈0.17，≈1.41，结果精确到‎0.1cm)‎ ‎25．(12分)定义：如图①，抛物线y＝ax2＋bx＋c(a≠0)与x轴交于A，B两点，点P在该抛物线上(P点与A、B两点不重合)．如果△ABP的三边满足AP2＋BP2＝AB2，则称点P为抛物线y＝ax2＋bx＋c(a≠0)的勾股点．‎ ‎(1)直接写出抛物线y＝－x2＋1的勾股点的坐标．‎ 8‎ ‎(2)如图②，已知抛物线y＝ax2＋bx(a≠0)与x轴交于A，B两点，点P(1，)是抛物线的勾股点，求抛物线的函数表达式．‎ ‎(3)在(2)的条件下，点Q在抛物线上，求满足条件S△ABQ＝S△ABP的Q点(异于点P)的坐标．‎ 参考答案与解析 ‎1．B　2.D　3.B　4.D　5.D　6.C　7.D　8.D　9.C ‎10．B　解析：∵抛物线y1＝(x＋1)2＋1与y2＝a(x－4)2－3交于点A(1，3)，∴3＝a 8‎ ‎(1－4)2－3，解得a＝，故①正确；∵E是抛物线的顶点，∴AE＝EC，∴无法得出AC＝AE，故②错误；当y＝3时，3＝(x＋1)2＋1，解得x1＝1，x2＝－3，故B(－3，3)，D(－1，1)，则AB＝4，AD＝BD＝2，∴AD2＋BD2＝AB2，∴△ABD是等腰直角三角形，故③正确；若(x＋1)2＋1＝(x－4)2－3，解得x1＝1，x2＝37，∴当37＞x＞1时，y1＞y2，故④错误．故选B.‎ ‎11．25°‎　12.1.2‎×108　13.1　14.1　5　15.1或　16.75°‎ ‎17.　解析：画树状图得：‎ ‎∵共有12种等可能的结果，点(m，n)恰好在反比例函数y＝图象上的有(2，3)，(－1，－6)，(3，2)，(－6，－1)，∴点(m，n)在函数y＝图象上的概率是＝.‎ ‎18.　解析：如图所示，根据点A在反比例函数y＝的图象上，且点A的横坐标是2，可得A.根据矩形和双曲线的对称性可得B，D，由两点间距离公式可得AB＝＝，AD＝＝，∴S矩形ABCD＝AB·AD＝×＝.‎ ‎19．解：(1)原式＝－4＋1＝1－3.(4分)‎ ‎(2)方程两边同乘以2x(x－3)得，x－3＝4x，解得x＝－1.(6分)检验：当x＝－1时，2x(x－3)≠0，∴原方程的根是x＝－1.(8分)‎ ‎20．解：CD∥AB，CD＝AB，(2分)证明如下：∵CE＝BF，∴CE－EF＝BF－EF，∴CF＝BE.(3分)在△DFC和△AEB中，∴△DFC≌△AEB(SAS)，(6分)∴CD＝AB，∠C＝∠B，∴CD∥AB.(8分)‎ 8‎ ‎21．解：(1)500　12　32(3分)‎ ‎(2)对“社会主义核心价值观”达到“A.非常了解”的人数为32%×500＝160(人)，补全条形统计图如下．(5分)‎ ‎(3)100000×32%＝32000(人)．‎ 答：该市大约有32000人对“社会主义核心价值观”达到“A.非常了解”的程度．(8分)‎ ‎22．解：(1)设第一批购进蒜薹x吨，第二批购进蒜薹y吨．由题意解得(3分)‎ 答：第一批购进蒜薹20吨，第二批购进蒜薹80吨．(4分)‎ ‎(2)设精加工m吨，总利润为w元，则粗加工(100－m)吨．由题意得m≤3(100－m)，解得m≤75，(6分)则利润w＝‎1000m＋400(100－m)＝‎600m＋40000.(8分)∵600＞0，∴w随m的增大而增大，∴m＝75时，w有最大值为85000元．‎ 答：精加工数量为75吨时，获得最大利润，最大利润为85000元．(10分)‎ ‎23．证明：(1)由圆周角定理得∠B＝∠E.∵∠B＝∠D，∴∠E＝∠D.(2分)∵CE∥AD，∴∠D＋∠ECD＝180°，∴∠E＋∠ECD＝180°，∴AE∥CD，∴四边形AECD为平行四边形．(5分)‎ ‎(2)作OM⊥BC于M，ON⊥CE于N.∵四边形AECD为平行四边形，∴AD＝CE.∵AD＝BC，∴CE＝CB.(7分)∵OM⊥BC，ON⊥CE，∴CN＝CM.在Rt△NOC和Rt△MOC中，∴Rt△NOC≌Rt△MOC，∴∠NCO＝∠MCO，∴CO平分∠BCE.(10分)‎ 24． 解：(1)如图，过点F作FN⊥DK于N，过点E作EM⊥FN于M.∵EF＋FG＝‎166cm，FG＝‎100cm，∴EF＝‎66cm.∵∠FGK＝80°，∴FN＝100·sin80°≈‎98cm.(2分)∵∠EFG＝125°，∴∠EFM＝180°－125°－10°＝45°，∴FM＝66·cos45°≈‎46.53cm，∴MN＝FN＋FM≈‎144.5cm.∴此时小强头部E点与地面DK相距约为‎144.5cm.(5分)‎ ‎(2)如图，过点E作EP⊥AB于点P，延长OB交MN于H.∵AB＝‎48cm，O为AB中点，∴AO＝BO＝‎24cm.∵EM＝66·sin45°≈46.53(cm)，∴PH≈46.53(cm)．(7分)∵GN＝100·cos80°≈17(cm)，CG＝‎15cm，∴OH＝24＋15＋17＝56(cm)，OP＝OH－PH＝56－46.53＝9.47≈‎9.5cm，∴他应向前‎9.5cm.(10分)‎ ‎25．解：(1)抛物线y＝－x2＋1的勾股点的坐标为(0，1)．(3分)‎ 8‎ ‎(2)如图，作PG⊥x轴于点G.∵点P的坐标为(1，)，∴AG＝1，PG＝，∴PA＝＝＝2.∵tan∠PAB＝＝，∴∠PAG＝60°.在Rt△PAB中，AB＝＝＝4，∴点B的坐标为(4，0)．(5分)设y＝ax(x－4)，将点P(1，)代入得a＝－，∴y＝－x(x－4)＝－x2＋x.(7分)‎ ‎(3)①当点Q在x轴上方时，由S△ABQ＝S△ABP知点Q的纵坐标为，则有－x2＋x＝，解得x1＝3，x2＝1(不符合题意，舍去)，∴点Q的坐标为(3，)．(9分)②当点Q在x轴下方时，由S△ABQ＝S△ABP知点Q的纵坐标为－，则有－x2＋x＝－，解得x1＝2＋，x2＝2－，∴点Q的坐标为(2＋，－)或(2－，－)．(11分)综上所述，满足条件的点Q有3个，分别为(3，)或(2＋，－)或(2－，－)．(12分)‎ 8‎