- 2021-04-15 发布 |
- 37.5 KB |
- 7页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
中考数学复习专题 代数式
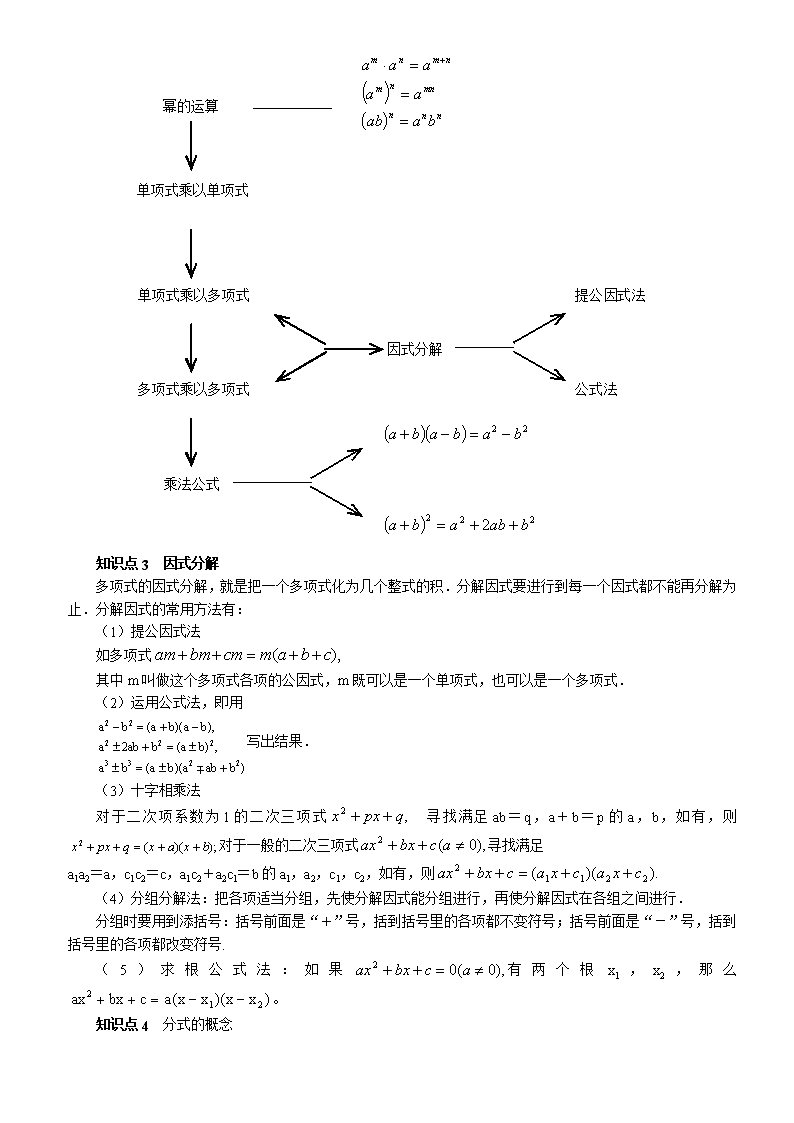
中考数学复习专题 代数式 一. 教学目标: 1. 复习整式的有关概念,整式的运算 2. 理解因式分解的概念,掌握提取公因式法、公式法、分组分解法等因式分解方法,能把简单多项式分解因 式。 3. 掌握分式的概念、性质,掌握分式的约分、通分、混合运算。 4. 理解平方根、立方根、算术平方根的概念,会用根号表示数的平方根、立方根和算术平方根。会求实数的 平方根、算术平方根和立方根,了解二次根式、最简二次根式、同类二次根式的概念,会辨别最简二次根式和 同类二次根式。掌握二次根式的性质,会化简简单的二次根式,能根据指定字母的取值范围将二次根式化简; 掌握二次根式的运算法则,能进行二次根式的加减乘除四则运算,会进行简单的分母有理化。 二. 教学重点、难点: 因式分解法在整式、分式、二次根式的化简与混合运算中的综合运用。 三.知识要点: 知识点 1 整式的概念 (1)整式中只含有一项的是单项式,否则是多项式,单独的字母或常数是单项式; (2)单项式的次数是所有字母的指数之和; 多项式的次数是多项式中最高次项的次数; (3)单项式的系数,多项式中的每一项的系数均包括它前面的符号 (4)同类项概念的两个相同与两个无关: 两个相同:一是所含字母相同,二是相同字母的指数相同; 两个无关:一是与系数的大小无关,二是与字母的顺序无关; (5)整式加减的实质是合并同类项; (6)因式分解与整式乘法的过程恰为相反。 知识点 2 整式的运算 (如结构图) 升降幂排列系数项数多项式的次数多项式 系数单项式的次数单项式整式 ———— —— 知识点 3 因式分解 多项式的因式分解,就是把一个多项式化为几个整式的积.分解因式要进行到每一个因式都不能再分解为 止.分解因式的常用方法有: (1)提公因式法 如多项式 其中 m 叫做这个多项式各项的公因式,m 既可以是一个单项式,也可以是一个多项式. (2)运用公式法,即用 写出结果. (3)十字相乘法 对于二次项系数为 l 的二次三项式 寻找满足 ab=q,a+b=p 的 a,b,如有,则 对于一般的二次三项式 寻找满足 a1a2=a,c1c2=c,a1c2+a2c1=b 的 a1,a2,c1,c2,如有,则 (4)分组分解法:把各项适当分组,先使分解因式能分组进行,再使分解因式在各组之间进行. 分组时要用到添括号:括号前面是“+”号,括到括号里的各项都不变符号;括号前面是“-”号,括到 括号里的各项都改变符号. ( 5 ) 求 根 公 式 法 : 如 果 有 两 个 根 x1 , x2 , 那 么 。 知识点 4 分式的概念 ),( cbamcmbmam ++=++ )baba)(ba(ba ,)ba(bab2a ),ba)(ba(ba 2233 222 22 +±=± ±=+± −+=− ,2 qpxx ++ );)((2 bxaxqpxx ++=++ ),0(2 ≠++ acbxax ).)(( 2211 2 cxacxacbxax ++=++ ),0(02 ≠=++ acbxax )xx)(xx(acbxax 21 2 −−=++ 单项式乘以单项式 单项式乘以多项式 多项式乘以多项式 ( ) ( ) nnn mnnm nmnm baab aa aaa = = =⋅ + 幂的运算 乘法公式 因式分解 提公因式法 公式法 ( )( ) 22 bababa −=−+ 提公因式法 ( ) 222 2 bababa ++=+ (1)分式的定义:整式 A 除以整式 B,可以表示成 的形式。如果除式 B 中含有字母,那么称 为分 式,其中 A 称为分式的分子,B 为分式的分母。 对于任意一个分式,分母都不能为零。 (2)分式的约分 (3)分式的通分 知识点 5 分式的性质 (1) (2)已知分式 ,分式的值为正:a 与 b 同号;分式的值为负:a 与 b 异号;分式的 值为零:a=0 且 b 0;分式有意义:b 0。 (3)零指数 (4)负整数指数 (5)整数幂的运算性质 上述等式中的 m、n 可以是 0 或负整数. 知识点 6 根式的有关概念 1. 平方根:若 x2=a(a>0),则 x 叫做 a 的平方根,记为 。 注意:①正数的平方根有两个,它们互为相反数;②0 的平方根是 0;③负数没有平方根; 2. 算术平方根:一个数的正的平方根叫做算术平方根; 3. 立方根:若 x3=a(a>0),则 x 叫做 a 的立方根,记为 。 4. 最简二次根式 被开方数所含因数是整数,因式是整式,不含能开得尽方的因数或因式的二次根式,叫做最简二次根式。 5. 同类二次根式:化简后被开方数相同的二次根式。 知识点 7 二次根式的性质 ① 是一个非负数; ② ③ ④ ⑤ 知识点 8 二次根式的运算 (1)二次根式的加减 二次根式相加减,先把各个二次根式化成最简二次根式,再把同类二次根式分别合并. (2)二次根式的乘法 二次根式相乘,等于各个因式的被开方数的积的算术平方根,即 二次根式的和相乘,可参照多项式的乘法进行. 两个含有二次根式的代数式相乘,如果它们的积不含有二次根式,那么这两个二次根式互为有理化因 式. (3)二次根式的除法 二次根式相除,通常先写成分式的形式,然后分子、分母都乘以分母的有理化因式,把分母的根号化去 B A B A )0( ≠= mB A Bn Am b a ≠ ≠ )0(10 ≠= aa ).p,0a( a 1a p p 为正整数≠=− nnn mnnm nmnm nmnm ba)ab( ,a)a( ),0a(aaa ,aaa = = ≠=÷ =⋅ − + a± 3 a )0( ≥aa )0()( 2 ≥= aaa <− = > == )0a(a )0a(0 )0a(a |a|)a( 2 )0,0( >≥= ba b a b a )0,0( ≥≥⋅= babaab ).0b,0a(abba ≥≥=⋅ (或分子、分母约分).把分母的根号化去,叫做分母有理化. 例 1. 如果单项式 与 的和①为 0 时,a、m、n 各为多少? ②仍为一个单项式,a、m、n 各为多少? 解:① ② a 为有理数 例 2. 因式分解:(1) (2) (3)-2x2+5xy+2y2 解:①原式=m(2x+3y)(2x-3y) ②原式 ③令 ∴ ∴ 原式=-2(x- )(x- ) 例 3. (1)已知 的结果中不含 项,求 k 的值; (2) 的一个因式是 ,求 k 的值; 解:(1)a2 的系数为:3k-2=0 ∴k= (2)当 a=-1 时(-1)3-(-1)2+(-1)+k=0 ∴k=3 例 4. 利用简便方法计算:(2+1)(22+1)(24+1)(28+1)(216+1)(232+1)的值, 你能确定积的个位数是几吗? 解:(2+1)(22+1)(24+1)(28+1)(216+1)(232+1) =264-1 ∵264 的个位数为 6 ∴积的个位数字为 5 例 5. x 为何值时,下列分式的值为 0?无意义? (1) (2) 解:当①x=2 ②x=1 时为零 当③x=-2 ④x=2,x=-1 时分式无意义 例 6. 分式的约分与通分 1. 约分: 2. 通分 , , 解:①原式= ② , , 例 7. 先化简后再求值: ,其中 原式= × + = + = 当 x= +1 时,原式=1 例 8. 若最简二次根式 是同类二次根式,求 a 的值。 解:1+a=4a2-2=0, a1=1 , a2=- 例题精讲 13 −nm yax 525 yx m−− =− −= = 51n3 m2m 5a = = = 2n 1m 5a =− −= 51n3 m2m = = 2n 1m 22 94 mymx − 1)(2)( 2 ++++ baba 2)1ba( ++= 0y2xy5x2 22 =++− 4 y16y25y5x 22 − +±−= y4 415x ±= y4 415+ y4 415− ))(123( 2 kaaa ++− 2a kaaa ++− 23 1+a 3 2 2 2 + − x x 2 23 2 2 −− +− xx xx 1n21n2 1n2n2 yx4.1 yx8.0 +− − cb5 a4 2 ba10 c3 2 2ac2 b5 − 2y7 x4 222 3 10 8 cba ca 222 3 10 3 Cba bc 222 3 10 25 cba ab− 1x 1 1x2x 3x2x 1x 3x 2 2 2 ++ ++ −−÷ − − 12x += )1)(1( 3 −+ − xx x )3)(1( )1( 2 −+ + xx x 1 1 +x 1 1 −x 1 1 +x 1 2 2 −x x 2 24312 1 2 −+− aa与 4 3 例 9. 已知:a= ,求 值 解:∵a= ∴a=2- <1 原式= +1 = -(a-1)+1 = -a+1+1= -a+2 当 a= 时,a=2- , ∴原式=-2- -2+ +2=-2 例 10. 把根号外的因式移到根号内: (1) ; (2) ; (3) ; (4) 解:(1)原式= (2)原式= (3)原式= (4)原式= 例 11. 观察下列各式及其验证过程 2 。验证: 3 。验证: 根据上述两个等式及其验证过程的基本思路,猜想 4 的变形结果并进行验证。 针对上述各式反映的规律,写出用 n(n 为任意自然数,且 n≥2)表示的等式,并给出证明。 解:(1) (2) 一. 选择题 1. 下列运算正确的是( ) A. B. C. D. 2. 把 a2-a-6 分解因式,正确的是( ) A. a(a-1)-6 B. (a-2)(a+3) C. (a+2)(a-3) D. (a-1)(a+6) 3. 设(x+y)(x+2+y)-15=0,则 x+y 的值是( ) A. -5 或 3 B. -3 或 5 C. 3 D. 5 4. 不论a为何值,代数式-a2+4a-5 的值( ) A. 大于或等于 0 B. 0 C. 大于 0 D. 小于 0 5. 化简二次根式 的结果是( ) A. B. C. D. 6. 下列命题:(1)任何数的平方根都有两个(2)如果一个数有立方根,那么它一定有平方根(3)算术平 方根一定是正数(4)非负数的立方根不一定是非负数,错误的个数为( ) A. 1 B. 2 C. 3 D. 4 7. 当 1查看更多
相关文章
- 当前文档收益归属上传用户
- 下载本文档