- 2021-04-15 发布 |
- 37.5 KB |
- 11页
申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
育英学校四年制初一第二学期数学期中练习 2017 年 4 月
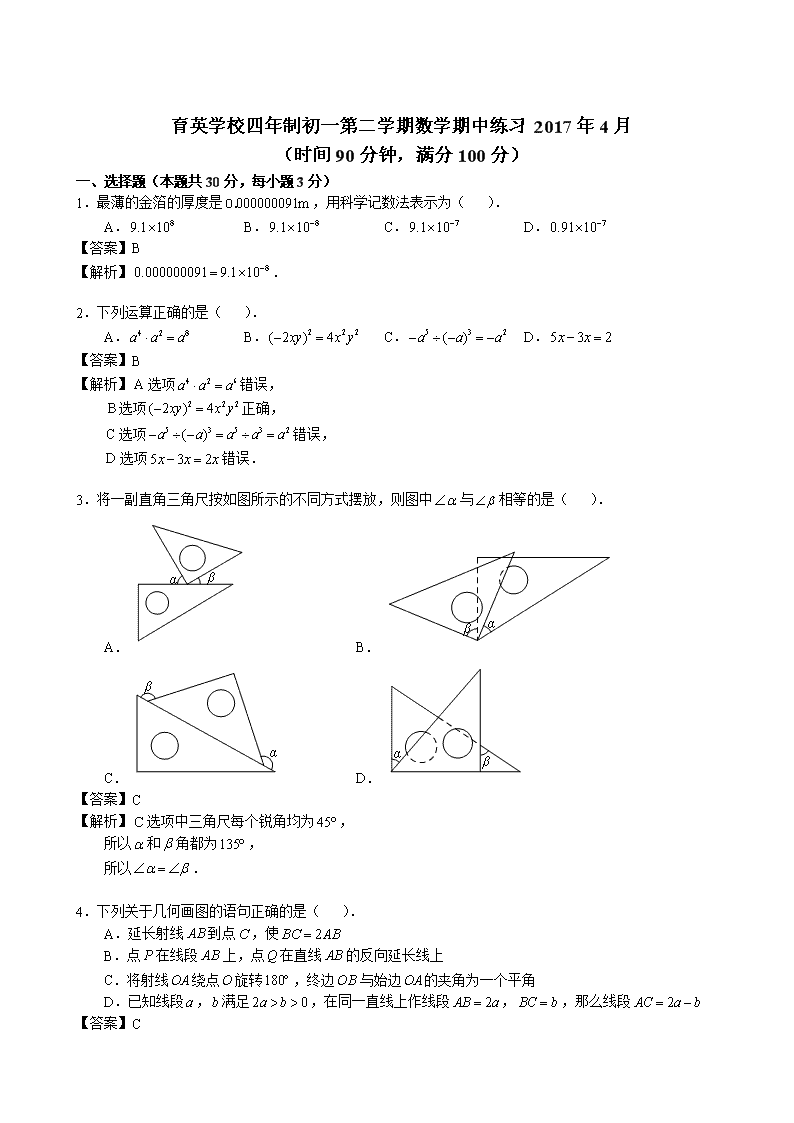
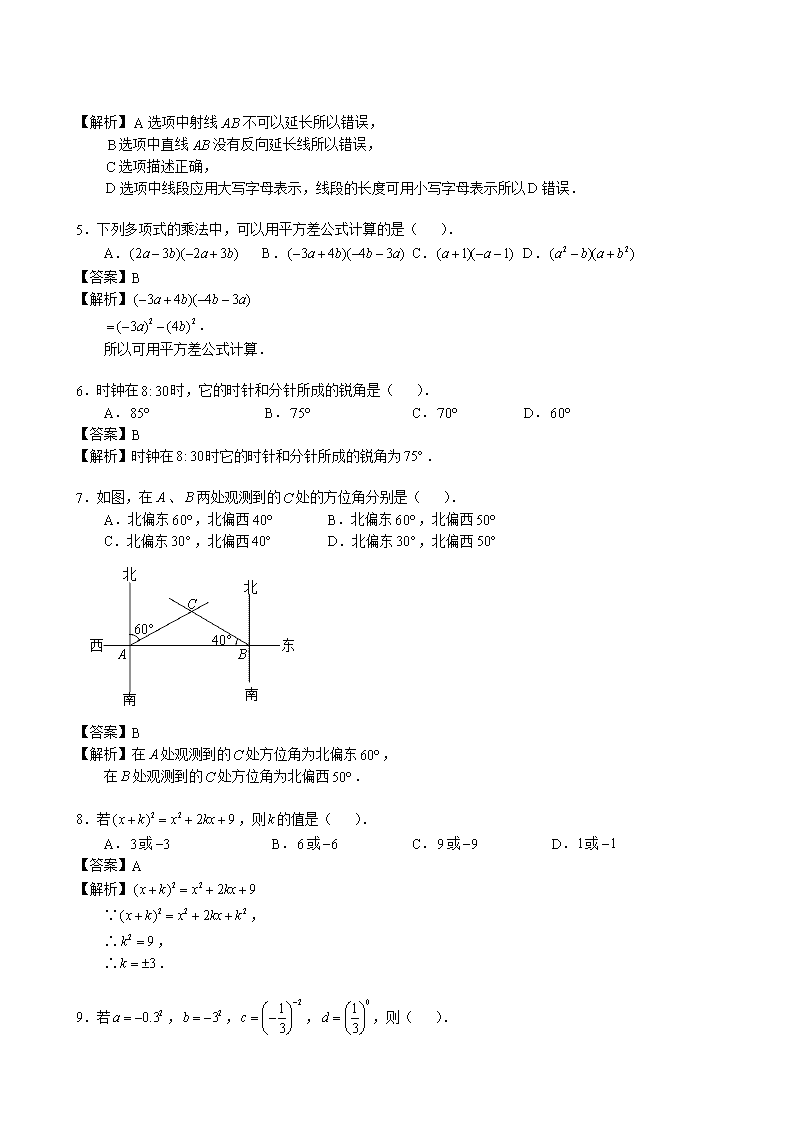
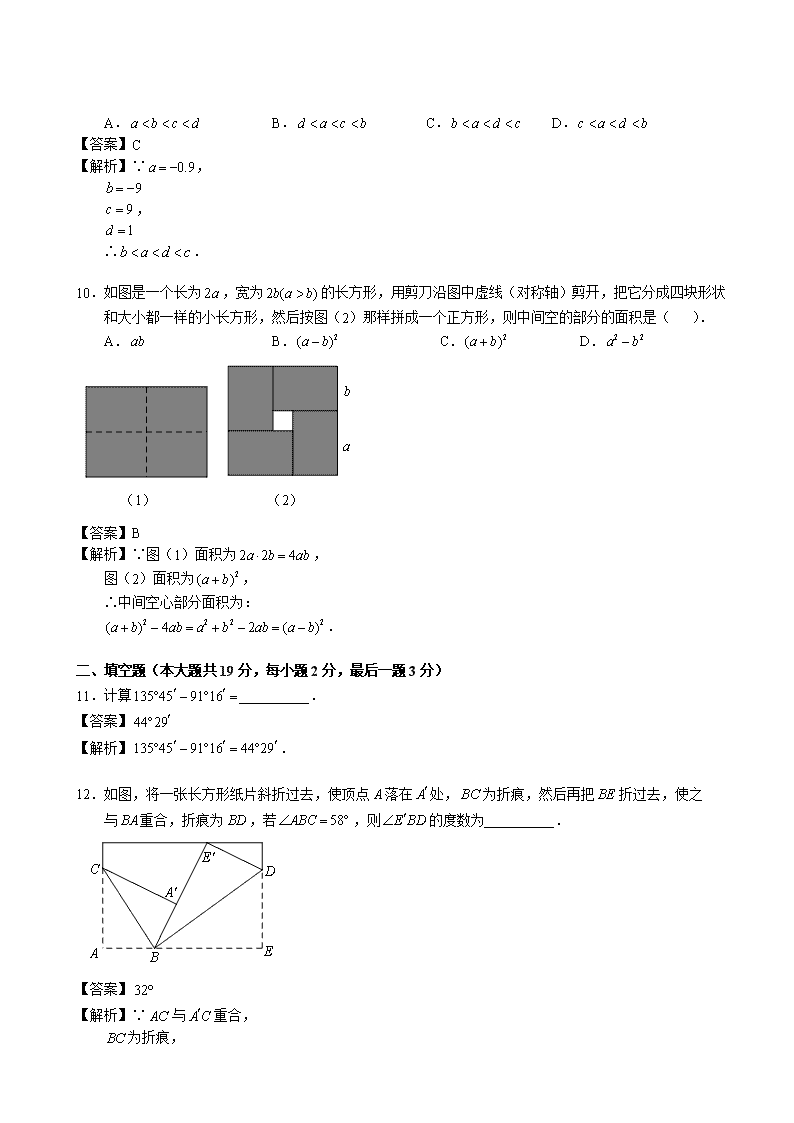
育英学校四年制初一第二学期数学期中练习 2017 年 4 月 (时间 90 分钟,满分 100 分) 一、选择题(本题共 30 分,每小题 3 分) 1.最薄的金箔的厚度是 000000091m0. ,用科学记数法表示为( ). A. 89.1 10 B. 89.1 10 C. 79.1 10 D. 70.91 10 【答案】B 【解析】 80.000000091 9.1 10 . 2.下列运算正确的是( ). A. 4 2 8a a a B. 2 2 2( 2 ) 4xy x y C. 5 3 2( )a a a D. 5 3 2x x 【答案】B 【解析】A选项 4 2 6a a a 错误, B选项 2 2 2( 2 ) 4xy x y 正确, C选项 5 3 5 3 2( )a a a a a 错误, D选项 5 3 2x x x 错误. 3.将一副直角三角尺按如图所示的不同方式摆放,则图中 与 相等的是( ). A. B. C. D. 【答案】C 【解析】C选项中三角尺每个锐角均为 45, 所以 和 角都为135, 所以 . 4.下列关于几何画图的语句正确的是( ). A.延长射线 AB到点C,使 2BC AB B.点 P在线段 AB上,点Q在直线 AB的反向延长线上 C.将射线OA绕点O旋转180,终边OB与始边OA的夹角为一个平角 D.已知线段 a, b满足 2 0a b ,在同一直线上作线段 2AB a , BC b ,那么线段 2AC a b 【答案】C 【解析】A选项中射线 AB不可以延长所以错误, B选项中直线 AB没有反向延长线所以错误, C选项描述正确, D选项中线段应用大写字母表示,线段的长度可用小写字母表示所以D错误. 5.下列多项式的乘法中,可以用平方差公式计算的是( ). A. ( )(2 3 2 )3a b a b B. ( )(3 4 4 3 )a b b a C. ( 1)( 1)a a D. 2 2( )( )a b a b 【答案】B 【解析】 ( )(3 4 4 3 )a b b a 2 2( 3 ) (4 )a b . 所以可用平方差公式计算. 6.时钟在8:30时,它的时针和分针所成的锐角是( ). A.85 B. 75 C. 70 D. 60 【答案】B 【解析】时钟在8:30时它的时针和分针所成的锐角为 75. 7.如图,在 A、 B两处观测到的C处的方位角分别是( ). A.北偏东 60,北偏西 40 B.北偏东 60,北偏西 50 C.北偏东 30,北偏西 40 D.北偏东 30,北偏西 50 【答案】B 【解析】在 A处观测到的C处方位角为北偏东 60, 在 B处观测到的C处方位角为北偏西 50. 8.若 2 2( ) 2 9x k x kx ,则 k的值是( ). A. 3或 3 B. 6或 6 C.9或 9 D.1或 1 【答案】A 【解析】 2 2( ) 2 9x k x kx ∵ 2 2 2( ) 2x k x kx k , ∴ 2 9k , ∴ 3k . 9.若 20.3a , 23b , 21 3 c , 01 3 d ,则( ). A. a b c d B. d a c b C. b a d c D. c a d b 【答案】C 【解析】∵ 0.9a , 9b 9c , 1d ∴ b a d c . 10.如图是一个长为 2a,宽为 2 ( )b a b 的长方形,用剪刀沿图中虚线(对称轴)剪开,把它分成四块形状 和大小都一样的小长方形,然后按图(2)那样拼成一个正方形,则中间空的部分的面积是( ). A. ab B. 2( )a b C. 2( )a b D. 2 2a b 【答案】B 【解析】∵图(1)面积为 2 2 4a b ab , 图(2)面积为 2( )a b , ∴中间空心部分面积为: 2 2 2 2( ) 4 2 ( )a b ab a b ab a b . 二、填空题(本大题共 19 分,每小题 2 分,最后一题 3 分) 11.计算135 45 91 16 __________. 【答案】 44 29 【解析】135 45 91 16 44 29 . 12.如图,将一张长方形纸片斜折过去,使顶点 A落在 A处, BC为折痕,然后再把 BE 折过去,使之 与 BA重合,折痕为 BD,若 58ABC ,则 E BD 的度数为__________. 【答案】 32 【解析】∵ AC与 AC 重合, BC为折痕, BE 与 BE重合, BD为折痕, ∴ 58ABC A BC , E BD EBD , ∴ 2 58 2 180E BD , ∴ 32E BD . 13.若点 B在直线 AC上, 12AB , 7BC ,则 A、C两点之间的距离是__________. 【答案】 5或19 【解析】当点 B在线段 AC中间时, 12AB , 7BC , ∴ 12 7 19AC , 当点C在线段 AB上时, 12AB , 7BC , ∴ 12 7 5AC . 综上得 A、C两点间距离为 5或19. 14.化简: ( 3)( 3) 9x x __________. 【答案】 2x 【解析】 ( 3)( 3) 9x x 2 9 9x 2x . 15.计算:若 2 1 2017 20173 ( 0.25) ( 4)x ,则 x __________. 【答案】 1 2 x 【解析】∵ 2 1 2017 20173 ( 0.25) ( 4)x 又∵ 2017 2017( 0.25) ( 4) 2017 20171 ( 4) 4 2017 1 ( 4) 4 20171 1 . ∴ 2 13 1x ∴ 2 1 0x 2 1x 1 2 x . 16.一张长为 4a厘米的矩形纸片的面积为 2(8 4 )a b a 平方厘米,则此矩形的宽为__________厘米. 【答案】 2 1ab 【解析】设矩形的宽为 x, ∴ 24 8 4a x a b a 2(8 4 ) 4x a b a a 2 1ab 17.已知 3mx , 4nx ,则 3 2m mx __________. 【答案】 27 16 【解析】∵ 3 2 3 2m n m nx x x 3 2( ) ( )m nx x 又∵ 3mx , 4nx , ∴ 3 2( ) ( )m nx x 3 2( 3) ( 4) 27 16 27 16 . ∴ 3 2 27 16 m nx . 18.如果一个多边形从一个顶点出发的对角线将这个多边形分成 7个三角形,则这个多边形一共有 __________条对角线. 【答案】 27 【解析】设多边形有几条边, ∴ 2 7n , ∴ 9n , 1 9 (9 3) 27 2 , ∴ 9边形共有 27条对角线. 19.已知: 2 2 ( )( )a b a b a b ; 3 3 2 2( )( )a b a b a ab b ; 4 4 3 2 2 3( )( )a b a b a a b ab b ; 5 5 4 3 2 2 3 4( )( )a b a b a a b a b ab b 按此规律,则 6 6 ( )a b a b __________. 【答案】 5 4 3 2 3 4 5( )a a b a b a b ab b 【解析】根据规律可得: 6 6 5 4 3 2 3 4 5( )( )a b a b a a b a b a b ab b . 三、计算题(本大题共 24 分,每小题 4 分)(注:能用乘法公式的要用乘法公式计算) 20.196 204 【答案】 39984 【解析】196 204 (200 4)(200 4) 40000 16 39984 . 21. 2 0 20171 (π 3.14) ( 1) 2 【答案】 2 【解析】 2 0 20171 (π 3.14) ( 1) 2 4 1 1 2 . 22. 3 5 2 4 8( ) 3a a a a 【答案】 8a 【解析】 3 5 2 4 8( ) 3a a a a 8 8 83a a a 8 82 3a a 8a . 23. 12 4 3 3 4( ) ( 2 )y y y 【答案】 1218y 【解析】 12 4 3 3 4( ) ( 2 )y y y 12 12 1216y y y 1218y . 24. 3 5 4 4 3 2 3 2(15 10 20 ) (5 )x y x y x y x y 【答案】 3 23 2 4y xy 【解析】 3 5 4 4 3 2 3 2(15 10 20 ) (5 )x y x y x y x y 3 23 2 4y xy . 25. ( 2 )( 2)x y y x 【答案】 2 24 4x x y 【解析】 ( 2 )( 2)x y y x 2 22 2 2 4 2xy x x y x y xy y 2 24 4x x y . 四、解答题(本大题共 27 分,26、27 每题 6 分,28 题 7 分,29 题 8 分) 26.已知 2 4 1 0x x ,求代数式 2 2(2 3) ( )( )x x y x y y 的值. 【答案】12 【解析】解:原式 2 2 2 24 12 9x x x y y 23 12 9x x . 又∵ 2 4 1 0x x , ∴ 2 4 1x x , 23( 4 ) 3x x , ∴ 23 12 9x x 23( 4 ) 9x x 3 9 12 . 27.阅读下面材料,并仿照材料中的方法解决问题. 制造弯形管道时,经常要先按中心线计算“展直长度”(如图中虚线的长度),再下料,这就涉及到计算 弧长的问题. 我们知道,弧是圆的一部分,弧长就是圆周长的一部分。在半径是 R的圆中,因为 360的圆心角所对 的弧长就是圆的周长 2πC r ,所以1的圆心角所对的弧长就是 2π 360 r ,即 π 180 r ,于是 n的圆心角所对的弧长 就是 π 180 n rl . 问题(1)若圆弧的半径为12,所对的圆心角为 60,则它的弧长为__________. 由组成圆心角的两条半径和圆心角所对的弧围成的图形叫做扇形,扇形面积是圆面积的一部分.想一 想:仿照上面的方法,能否计算扇形的面积呢? 问题( 2)圆心角是1的扇形面积是__________. ( 3)如果用字母 S表示扇形的面积, n表示圆心角的度数, r 表示圆半径,那么扇形面积的计算公式 为: S __________. 【答案】(1) 4π ( 2) 2π 360 R ( 3) 2π 360 n rS 【解析】(1)弧长 60π 12 720π 4π 180 180 . ( 2) 2π 360 n R S 扇 【注意有文字】 ∴1的扇形面积为 2π 360 R . ( 3) 2π 360 n rS . 28.如图,己知平面内两点 A、 B. (1)用尺规按下列要求作图,井保留作图痕. ①连接 AB. ②在线段 AB的延长线上取点C,使 BC AB . ③在线段 BA的延长线上取点D,使 AD AC . ( 2)若 6AB , E是DB中点,求 EA的长度. 【答案】见解析 【解析】(1)①②③ ( 2)∵ 6AB 且 AB BC , ∴ 2 12AC AD AB . 又∵ 12AC , 6AB , ∴ 12 6 18BD AC AB , ∵ E为 BD中点, ∴ 1 9 2 DE BE BD , ∵ 12AD , 9DE , ∴ 3AE AD DE , 则: 3AE . 29.如图,射线OC以 AOB 的边OB为始边进行逆时针旋转,作OD平分 AOC ,OE平分 BOC , 在射线OC旋转过程中,试探究 DOE 与 BOC 的大小关系. (1)当 90AOB , 60BOC 时, DOE __________度. ( 2)设 90AOB , BOC n ①当 0 90n 时,在射线OC旋转过程中, DOE 的大小是否发生变化?若发生变化,请说明 DOE 的度数变化情况;若不发生变化,请求出 DOE 的度数. ②当 90 360n 时,在射线OC旋转过程中, DOE 的大小是否发生变化?若发生变化,请画图并 说明 DOE 的度数变化情况;若不发生变化,请说明理由; (注:作 BOC 的角平分线时,指的是作小于平角的那个 BOC 的平分线) 【答案】(1) 45 【解析】(1)∵ 90AOB , AOD DOC 且 COE EOB , ∴ 2 2 90DOC COE , ∴ 45DOC COE , ∴ 45DOE . ( 2)①当 0 90n 时, ∵OD平分 AOC , OE平分 BOC , ∴ DOE DOC EOC , 1 1 2 2 BOC AOC , 1 2 AOB 1 90 2 45 . ∴ DOE 不发生变化. ( 2)②解: Ⅰ:当 90 180n ≤ 时, ∵ BOC n , 90AOB , ∴ 2 nBOE COE , ∴ 90 2 nAOE , 1( ) 2 COD DOA COA AOE AOE , 1( ) 2 COE AOE 190 2 2 2 n n 45 2 n . ∴ DOE DOA AOE 45 90 2 2 n n 45 . Ⅱ:当180 270n ≤ 时, ∵ BOC n , 90AOB , ∴ 2 nBOE COE , 360 90 135 2 2 n nCOD DOA , ∴ DOE COD COE 135 2 2 n n 135 . Ⅲ:当 270 360n 时, ∵ BOC n , 90AOB , ∴ 2 nCOE BOE , 又∵ 90AOC n , ∴ 90 45 2 2 n nAOD DOC , ∴ DOB DOC BOC , 45 2 n n 45 2 n . ∴ DOE DOB BOE , 45 2 2 n n 45 . 综上可得:当 90 360n 时, DOE 的度数发生变化.查看更多