- 2021-04-15 发布 |
- 37.5 KB |
- 13页

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2021届新高考版高考数学一轮复习课件:§1-1 集合(讲解部分)
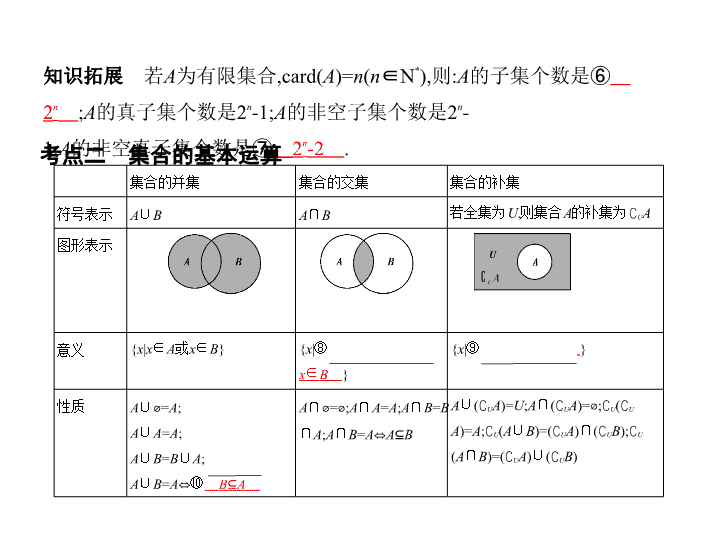
考点一 集合及其关系 1.集合的含义与表示 (1)集合中元素的三个特性:确定性、互异性、① 无序性 . (2)集合中元素与集合的关系有且仅有两种:属于(用符号“∈”表示)和不 属于(用符号“ ∉ ”表示). (3)常用数集及其符号表示 (4)集合常用的表示方法:列举法、④ 描述法 、Venn图法. 名称 非负整数集 (自然数集) 正整数集 整数集 有理数集 实数集 符号 ② N N * 或N + ③ Z Q R 考点清单 注意 集合元素互异性的应用:(1)利用集合元素的互异性找到解题的切入 点;(2)在解答完毕时,注意检查集合的元素是否满足互异性,以确保答案正确. 2.集合间的基本关系 表示关系 定义 记法 集合 间的 基本 关系 相等 集合 A 与集合 B 中的所有元素都相同 A = B 子集 集合 A 中任意一个元素均为集合 B 中的元素 A ⊆ B (或 B ⊇ A ) 真子集 集合 A 中任意一个元素均为集合 B 中的元素,且 B 中至少有一个元素 A 中没有 A ⫋ B (或 B ⫌ A ) 空集 空集是任何集合的子集 ⌀⊆ B 空集是任何⑤ 非空 集合的真子集 ⌀⫋ B ( B ≠ ⌀ ) 注意 遇到形如 A ⊆ B 的问题,要优先考虑 A = ⌀ 是否满足题意. 知识拓展 若 A 为有限集合,card( A )= n ( n ∈N * ),则: A 的子集个数是⑥ 2 n ; A 的真子集个数是2 n -1; A 的非空子集个数是2 n -1; A 的非空真子集个数是⑦ 2 n -2 . 考点二 集合的基本运算 集合的并集 集合的交集 集合的补集 符号表示 A ∪ B A ∩ B 若全集为 U ,则集合 A 的补集为 ∁ U A 图形表示 意义 { x | x ∈ A 或 x ∈ B } { x |⑧ x ∈ A ,且 x ∈ B } { x |⑨ x ∈ U ,且 x ∉ A } 性质 A ∪ ⌀ = A ; A ∪ A = A ; A ∪ B = B ∪ A ; A ∪ B = A ⇔ ⑩ B ⊆ A A ∩ ⌀ = ⌀ ; A ∩ A = A ; A ∩ B = B ∩ A ; A ∩ B = A ⇔ A ⊆ B A ∪ ( ∁ U A )= U ; A ∩ ( ∁ U A )= ⌀ ; ∁ U ( ∁ U A )= A ; ∁ U ( A ∪ B )=( ∁ U A ) ∩ ( ∁ U B ); ∁ U ( A ∩ B )=( ∁ U A ) ∪ ( ∁ U B ) 考法一 集合间基本关系的求解方法 知能拓展 例1 (1)(2019湖北天门调研,1)集合 M = x , N = ,则 ( ) A. M = N B. M ⫋ N C. N ⫋ M D. M 与 N 没有相同的元素 (2)(2018中原名校联考,2)已知集合 A ={ x | y =lg( x - x 2 )}, B ={ x | x 2 - cx <0, c >0},若 A ⊆ B ,则实数 c 的取值范围为 ( ) A.(0,1] B.[1,+ ∞ ) C.(0,1) D.(1,+ ∞ ) 解题导引 (1)化简两集合,观察两集合中元素的构成特征,再确定两个集 合的关系,得出结果. (2)思路一:首先化简两集合,利用 A ⊆ B 确定两集合端点值的大小关系,结合 数轴得出实数 c 的取值范围. 思路二:首先化简集合 A ,然后对 c 取特殊值,运用排除法,从而得出正确答案. 解析 (1)集合 M = = x x = (2k+1),k∈Z , N = = x x= (k+2),k∈Z ,当 k ∈Z时,2 k +1是奇数, k +2是整 数,又知奇数均为整数,而整数不一定为奇数,所以 M ⫋ N ,故选B. (2)解法一:由题意知, A ={ x | y =lg( x - x 2 )}={ x | x - x 2 >0}={ x |0< x <1}, B ={ x | x 2 - cx < 0, c >0}={ x |0< x < c }.由 A ⊆ B ,画出数轴,如图所示,得 c ≥ 1,故选B. 解法二: A ={ x | y =lg( x - x 2 )}={ x | x - x 2 >0}={ x |0< x <1},取 c =1,得 B ={ x |0< x <1},则 A ⊆ B 成立,可排除C、D;取 c =2,得 B ={ x |0< x <2},则 A ⊆ B 成立,可排除A,故选B. 答案 (1)B (2)B 方法总结 1.判断两集合的关系一般有两种方法:一是化简集合,从其中直 接寻找两集合的关系;二是用列举法(或Venn图法)表示各个集合,从元素 (或图形)中寻找关系. 2.已知两集合间的关系求参数的取值范围时,关键是将两集合间的关系转 化为元素间的关系,进而转化为参数满足的关系.解决这类问题时常常需要 合理利用数轴、Venn图帮助分析. 考法二 集合运算问题的求解方法 例2 (1)(2019湖南重点中学摸底联考,1)已知全集 U ={1,2,3,4,5,6,7}, M ={3, 4,5}, N ={1,3,6},则集合{2,7}= ( ) A. M ∩ N B.( ∁ U M ) ∩ ( ∁ U N ) C.( ∁ U M ) ∪ ( ∁ U N ) D. M ∪ N (2)(2019重庆(区县)调研,1)已知全集 U =R,集合 A ={ x | x 2 + x -2 ≤ 0}, B ={ x | x <0}, 则( ∁ U A ) ∩ B = ( ) A.{ x | x <-1} B.{ x |-2 ≤ x <0} C.{ x | x <-2} D.{ x | x ≤ -1} 解题导引 (1)思路一:由已知集合,分别求出 ∁ U M , ∁ U N ,再验证选项. 思路二:根据集合 U , M , N 的关系画出Venn图,从而确定结论. (2)先求出集合 A ,再求出 ∁ U A ,借助于数轴求出( ∁ U A ) ∩ B . 解析 (1)解法一:∵ U ={1,2,3,4,5,6,7}, M ={3,4,5}, N ={1,3,6},∴ ∁ U M ={1,2,6, 7}, ∁ U N ={2,4,5,7}, M ∩ N ={3}, M ∪ N ={1,3,4,5,6},∴( ∁ U M ) ∩ ( ∁ U N )={2,7}, ( ∁ U M ) ∪ ( ∁ U N )={1,2,4,5,6,7},故选B. 解法二:由集合 M , N , U 的关系画出Venn图(如图所示). 由图可知 ∁ U ( M ∪ N )=( ∁ U M ) ∩ ( ∁ U N )={2,7},故选B. (2) A ={ x | x 2 + x -2 ≤ 0}={ x |-2 ≤ x ≤ 1}, U =R,∴ ∁ U A ={ x | x <-2或 x >1},又 B ={ x | x < 0},∴借助数轴可知( ∁ U A ) ∩ B ={ x | x <-2}.故选C. 答案 (1)B (2)C 方法总结 集合的基本运算包括集合的交、并、补运算,解决此类运算问 题一般应注意以下几点:一是看集合的表示方法,用列举法表示的集合,易 用Venn图求解,用描述法表示的数集,常借助数轴分析得出结果,二是对集 合进行化简,有些集合是可以化简的,通过化简集合,可使问题变得简单明 了,易于解决. 例 (2016北京文,16)某网店统计了连续三天售出商品的种类情况:第一天 售出19种商品,第二天售出13种商品,第三天售出18种商品;前两天都售出 的商品有3种,后两天都售出的商品有4种,则该网店: ①第一天售出但第二天未售出的商品有 种; ②这三天售出的商品最少有 种. 实践探究 解题导引 “网购”是现代购物的重要方式之一,本题以售出商品的种类 为背景,取材于人A必修113页的“阅读与思考——集合中元素的个数”, 考查了集合运算和Venn图等基本知识,同时也涉及化归与转化、数形结合 的数学思想. ①可以通过集合交、补运算确定元素个数;②中“三天共售出的商品种类 最少”应该是第三天与前二天售出的商品种类完全相同时,总的种类最少. 解析 ①设第一天售出的商品为集合 A ,则 A 中有19个元素,第二天售出的 商品为集合 B ,则 B 中有13个元素.由于前两天都售出的商品有3种,则 A ∩ B 中有3个元素.如图所示, 所以该网店第一天售出但第二天未售出的商品有19-3=16(种). ②由①知,前两天售出的商品为19+13-3=29(种),当第三天售出的18种都是 前两天售出的商品时,这三天售出的商品种类最少,售出的商品最少为29种. 答案 ①16 ②29 方法总结 本题实际上是把实际问题用集合的符号语言及图形语言表示 出来,体现数学的转化与化归思想,这与数学抽象,逻辑推理等学科核心素 养是紧密关联的,在强调核心素养的大环境下,需关注此类问题,关键是灵 活运用Venn图来分析、解决问题.查看更多