2020年高考真题+高考模拟题 专项版解析汇编 理科数学——06 三角函数及解三角形（教师版）

2020年高考真题+高考模拟题 专项版解析汇编 理科数学——06 三角函数及解三角形（教师版）

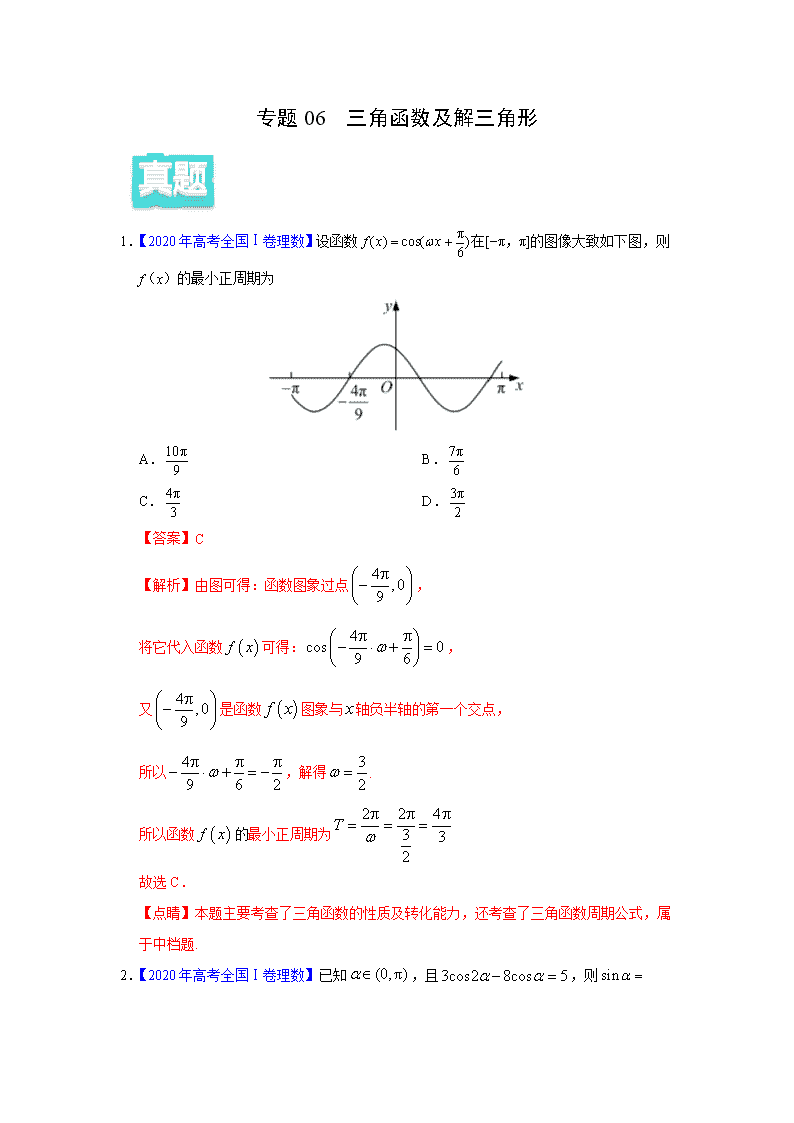
专题 06 三角函数及解三角形 1．【2020 年高考全国Ⅰ卷理数】设函数 在[−π，π]的图像大致如下图，则 f（x）的最小正周期为 A． B． C． D． 【答案】C 【解析】由图可得：函数图象过点 ， 将它代入函数 可得： ， 又 是函数 图象与 轴负半轴的第一个交点， 所以 ，解得 . 所以函数 最小正周期为 故选 C． 【点睛】本题主要考查了三角函数的性质及转化能力，还考查了三角函数周期公式，属 于中档题. 2．【2020 年高考全国Ⅰ卷理数】已知 ，且 ，则 的 π( ) cos( )6f x xω= + 10π 9 7π 6 4π 3 3π 2 4 ,09 π −   ( )f x 4cos 09 6 ωπ π − ⋅ + =   4 ,09 π −   ( )f x x 4 9 6 2 ωπ π π− ⋅ + = − 3 2 ω = ( )f x 2 2 4 3 3 2 T ω π π π= = = π( )0,α∈ 3cos2 8cos 5α α− = sinα = A． B． C． D． 【答案】A 【解析】 ，得 ， 即 ，解得 或 （舍去）， 又 . 故选：A． 【点睛】本题考查三角恒等变换和同角间的三角函数关系求值，熟记公式是解题的关键， 考查计算求解能力，属于基础题. 3．【2020 年高考全国Ⅱ卷理数】若 α 为第四象限角，则 A．cos2α>0 B．cos2α<0 C．sin2α>0 D．sin2α<0 【答案】D 【解析】方法一：由 α 为第四象限角，可得 ， 所以 此时 的终边落在第三、四象限及 轴的非正半轴上，所以 ， 故选：D． 方法二：当 时， ，选项 B 错误； 当 时， ，选项 A 错误； 由 在第四象限可得： ，则 ，选项 C 错 误，选项 D 正确； 故选：D． 【点睛】本题主要考查三角函数的符号，二倍角公式，特殊角的三角函数值等知识，意 5 3 2 3 1 3 5 9 3cos2 8cos 5α α− = 26cos 8cos 8 0α α− − = 23cos 4cos 4 0α α− − = 2cos 3 α = − cos 2α = 2 5(0, ), sin 1 cos 3 α α α∈ π ∴ = − = 3 2 2 2 ,2 k k kαπ + π < < π + π ∈Z 3 4 2 4 4 ,k k kαπ + π < < π + π ∈Z 2α y sin 2 0α < 6 α π= − cos2 cos 03 α π = − >   3 α π= − 2cos2 cos 03 α π = − <   α sin 0,cos 0α α< > sin 2 2sin cos 0α α α= < 在考查学生的转化能力和计算求解能力. 4.【2020 年高考全国 III 卷理数】在△ABC 中，cosC= ，AC=4，BC=3，则 cosB= A． B． C． D． 【答案】A 【解析】 在 中， ， ， ， 根据余弦定理： ， ， 可得 ，即 ， 由 ， 故 . 故选：A． 5．【2020 年高考全国Ⅲ卷理数】已知 2tanθ–tan(θ+ )=7，则 tanθ= A．–2 B．–1 C．1 D．2 【答案】D 【解析】 ， ， 令 ，则 ，整理得 ，解得 ，即 . 故选：D． 【点睛】本题主要考查了利用两角和的正切公式化简求值，属于中档题. 6．【2020 年高考北京】2020 年 3 月 14 日是全球首个国际圆周率日（ Day）．历史上，求 圆周率 的方法有多种，与中国传统数学中的“割圆术”相似．数学家阿尔·卡西的方法是： 2 3 1 9 1 3 1 2 2 3  ABC 2cos 3C = 4AC = 3BC = 2 2 2 2 cosAB AC BC AC BC C= + − ⋅ ⋅ 2 2 24 3 2 24 3 3AB = + − × × × 2 9AB = 3AB =  2 2 2 9 9 16 1cos 2 2 3 3 9 AB BC ACB AB BC + − + −= = =⋅ × × 1cos 9B = π 4 2tan tan 74 πθ θ − + =   tan 12tan 71 tan θθ θ +∴ − =− tan , 1t tθ= ≠ 12 71 tt t +− =− 2 4 4 0t t− + = 2t = tan 2θ = π π 当正整数 充分大时，计算单位圆的内接正 边形的周长和外切正 边形（各边均与 圆相切的正 边形）的周长，将它们的算术平均数作为 的近似值．按照阿尔·卡西的 方法， 的近似值的表达式是 A． B． C． D． 【答案】A 【解析】单位圆内接正 边形的每条边所对应的圆周角为 ，每条边长为 ， 所以，单位圆的内接正 边形的周长为 ， 单位圆的外切正 边形的每条边长为 ，其周长为 ， ， 则 . 故选：A． 【点睛】本题考查圆周率 的近似值的计算，根据题意计算出单位圆内接正 边形和外 切正 边形的周长是解答的关键，考查计算能力，属于中等题. 7．【2020 年新高考全国Ⅰ卷】下图是函数 y= sin(ωx+φ)的部分图像，则 sin(ωx+φ)= A． B． C． D． 【答案】BC n 6n 6n 6n 2π π 30 303 sin tann n n ° ° +   30 306 sin tann n n ° ° +   60 603 sin tann n n ° ° +   60 606 sin tann n n ° ° +   6n 360 60 6n n ° °=× 302sin n ° 6n 3012 sinn n ° 6n 302tan n ° 3012 tann n ° 30 3012 sin 12 tan 30 302 6 sin tan2 n nn n n n n π ° °+ ° ° ∴ = = +   30 303 sin tann n n π ° ° = +   π 6n 6n πsin( 3x + ） πsin( 2 )3 x− πcos(2 6x + ） 5πcos( 2 )6 x− 【解析】由函数图像可知： ，则 ，所以不选 A, 当 时， ， 解得： ， 即函数的解析式为： . 而 故选：BC． 【点睛】已知 f(x)＝Asin(ωx＋φ)(A＞0，ω＞0)的部分图象求其解析式时，A 比较容易看 图得出，困难的是求待定系数 ω 和 φ，常用如下两种方法： (1)由 ω＝ 即可求出 ω；确定 φ 时，若能求出离原点最近的右侧图象上升(或下降)的 “零点”横坐标 x0，则令 ωx0＋φ＝0(或 ωx0＋φ＝π)，即可求出 φ. (2)代入点的坐标，利用一些已知点(最高点、最低点或“零点”)坐标代入解析式，再结合 图形解出 ω 和 φ，若对 A，ω 的符号或对 φ 的范围有要求，则可用诱导公式变换使其符 合要求. 8.【2020 年高考全国Ⅰ卷理数】如图，在三棱锥 P–ABC 的平面展开图中，AC=1， ，AB⊥AC，AB⊥AD，∠CAE=30°，则 cos∠FCB=______________. 2 2 3 6 2 T π ππ= − = 2 2 2T π πω π= = = 2 53 6 2 12x ππ π+ = = 1y = − ∴ ( )5 32 212 2 k k Z π πϕ π× + = + ∈ ( )22 3k kϕ π π= + ∈Z 2sin 2 2 sin 2 cos 2 sin 23 6 2 6 3y x k x x x π π π ππ π       = + + = + + = + = −               5cos 2 cos( 2 )6 6x x π π + = − −   2 T π 3AB AD= = 【答案】 【解析】 ， ， ， 由勾股定理得 ， 同理得 ， ， 在 中， ， ， ， 由余弦定理得 ， ， 在 中， ， ， ， 由余弦定理得 . 故答案为： . 【点睛】本题考查利用余弦定理解三角形，考查计算能力，属于中等题. 9．【2020 年高考全国 III 卷理数】16.关于函数 f（x）= 有如下四个命题： ①f（x）的图像关于 y 轴对称． ②f（x）的图像关于原点对称． ③f（x）的图像关于直线 x= 对称． 1 4 − AB AC⊥ 3AB = 1AC = 2 2 2BC AB AC= + = 6BD = 6BF BD∴ = = ACE△ 1AC = 3AE AD= = 30CAE∠ =  2 2 2 32 cos30 1 3 2 1 3 12CE AC AE AC AE= + − ⋅ = + − × × × = 1CF CE∴ = = BCF 2BC = 6BF = 1CF = 2 2 2 1 4 6 1cos 2 2 1 2 4 CF BC BFFCB CF BC + − + −∠ = = = −⋅ × × 1 4 − 1sin sinx x + 2 π ④f（x）的最小值为 2． 其中所有真命题的序号是__________． 【答案】②③ 【 解 析 】 对 于 命 题 ① ， ， ， 则 ， 所以，函数 的图象不关于 轴对称，命题①错误； 对于命题②，函数 的定义域为 ，定义域关于原点对称， ， 所以，函数 的图象关于原点对称，命题②正确； 对于命题③， ， ，则 ， 所以，函数 的图象关于直线 对称，命题③正确； 对于命题④，当 时， ，则 ， 命题④错误. 故答案为：②③. 【点睛】本题考查正弦型函数的奇偶性、对称性以及最值的求解，考查推理能力与计算 能力，属于中等题. 10．【2020年高考江苏】已知 = ，则 的值是 ▲ ． 【答案】 1 526 2 2f π  = + =   1 526 2 2f π − = − − = −   6 6f f π π   − ≠       ( )f x y ( )f x { },x x k k Zπ≠ ∈ ( ) ( ) ( ) ( )1 1 1sin sin sinsin sin sinf x x x x f xx x x  − = − + = − − = − + = − −   ( )f x 1 1sin cos2 2 cossin 2 f x x x xx π π π    − = − + = +         −    1 1sin cos2 2 cossin 2 f x x x xx π π π    + = + + = +         +   2 2f x f x π π   − = +       ( )f x 2x π= 0xπ− < < sin 0x < ( ) 1sin 0 2sinf x x x = + < < 2sin ( )4 απ + 2 3 sin 2α 1 3 【解析】 故答案为： 【点睛】本题考查两角和正弦公式、二倍角正弦公式，考查基本分析求解能力，属基础 题. 11．【2020 年高考北京】若函数 的最大值为2，则常数 的一个取 值为________． 【答案】 （ 均可） 【 解 析 】 因 为 ， 所以 ，解得 ，故可取 . 故答案为： （ 均可）. 【点睛】本题主要考查两角和的正弦公式，辅助角公式的应用，以及平方关系的应用， 考查学生的数学运算能力，属于基础题. 12．【2020 年高考浙江】已知 ，则 _______， _______． 【答案】 ； 【解析】 ， ， 故答案为： 【点睛】本题考查二倍角余弦公式以及弦化切、两角差正切公式，考查基本分析求解能 力，属基础题. 2 22 2 1sin ( ) ( cos sin ) (1 sin 2 )4 2 2 2 π α α α α+ = + = + 1 2 1(1 sin 2 ) sin 22 3 3 α α∴ + = ∴ = 1 3 ( ) sin( ) cosf x x xϕ= + + ϕ 2 π 2 ,2k k Z ππ + ∈ ( ) ( ) ( ) ( )22cos sin sin 1 cos cos sin 1 sinf x x x xϕ ϕ ϕ ϕ θ= + + = + + + ( )22cos sin 1 2ϕ ϕ+ + = sin 1ϕ = 2 ϕ π= 2 π 2 ,2k k Z ππ + ∈ tan 2θ = cos2θ = πtan( )4 θ − = 3 5- 1 3 2 2 2 2 2 2 2 2 2 2 cos sin 1 tan 1 2 3cos2 cos sin cos sin 1 tan 1 2 5 θ θ θθ θ θ θ θ θ − − −= − = = = = −+ + + tan 1 2 1 1tan( )4 1 tan 1 2 3 π θθ θ − −− = = =+ + 3 1,5 3 − 13．【2020 年高考江苏】将函数 的图象向右平移 个单位长度，则平移后的 图象中与 y 轴最近的对称轴的方程是 ▲ ． 【答案】 【解析】 当 时 . 故答案为： 【点睛】本题考查三角函数图象变换、正弦函数对称轴，考查基本分析求解能力，属基 础题. 14．【2020 年新高考全国Ⅰ卷】某中学开展劳动实习，学生加工制作零件，零件的截面如图 所示．O 为圆孔及轮廓圆弧 AB 所在圆的圆心，A 是圆弧 AB 与直线 AG 的切点，B 是圆 弧 AB 与直线 BC 的切点，四边形 DEFG 为矩形，BC⊥DG，垂足为 C，tan∠ODC= ， ，EF=12 cm，DE=2 cm，A 到直线 DE 和 EF 的距离均为 7 cm，圆孔半径为 1 cm，则图中阴影部分的面积为________cm2． 【答案】 【解析】设 ，由题意 ， ，所以 ， 因为 ,所以 ， 因为 ，所以 ， 因为 与圆弧 相切于 点，所以 ， 即 为等腰直角三角形； πsin(3 2 )4y x= ﹢ π 6 5 24x π= − 3sin[2( ) ] 3sin(2 )6 4 12y x x π π π= − + = − 72 ( ) ( )12 2 24 2 kx k k Z x k Z π π π ππ− = + ∈ ∴ = + ∈ 1k = − 5 24x π= − 5 24x π= − 3 5 BH DG∥ 54 2 π+ = =OB OA r 7AM AN= = 12EF = 5NF = 5AP = 45AGP °∠ = //BH DG 45AHO °∠ = AG AB A OA AG⊥ OAH△ 在直角 中， ， ， 因为 ，所以 ， 解得 ； 等腰直角 的面积为 ； 扇形 的面积 ， 所以阴影部分的面积为 . 故答案为： . 【点睛】本题主要考查三角函数在实际中应用，把阴影部分合理分割是求解的关键，以 劳动实习为背景，体现了五育并举的育人方针. 15．【2020 年高考全国 II 卷理数】 中，sin2A－sin2B－sin2C= sinBsinC． （1）求 A； （2）若 BC=3，求 周长的最大值． 【解析】（1）由正弦定理和已知条件得 ，① 由余弦定理得 ，② OQD△ 25 2OQ r= − 27 2DQ r= − 3tan 5 OQODC DQ ∠ = = 3 2 5 221 252 2r r− = − 2 2r = OAH△ 1 1 2 2 2 2 42S = × × = AOB ( )2 2 1 3 2 2 32 4S π π= × × = 1 2 1 542 2S S ππ+ − = + 54 2 π+ ABC△ ABC△ 2 2 2BC AC AB AC AB− − = ⋅ 2 2 2 2 cosBC AC AB AC AB A= + − ⋅ 由①，②得 . 因为 ，所以 . （2）由正弦定理及（1）得 ， 从而 ， . 故 . 又 ，所以当 时， 周长取得最大值 . 16．【2020 年 高 考 江 苏 】 在△ABC 中 ， 角 A，B，C 的 对 边 分 别 为 a，b，c， 已 知 ． （1）求 的值； （2）在边 BC 上取一点 D，使得 ，求 的值． 【解析】（1）在 中，因为 ， 由余弦定理 ，得 ， 所以 . 在 中，由正弦定理 ， 得 ， 所以 （2）在 中，因为 ,所以 为钝角， 而 ,所以 为锐角. 故 则 . 1cos 2A = − 0 πA< < 2π 3A = 2 3sin sin sin AC AB BC B C A = = = 2 3sinAC B= 2 3sin(π ) 3cos 3sinAB A B B B= − − = − π3 3sin 3cos 3 2 3sin( )3BC AC AB B B B+ + = + + = + + π0 3B< < π 6B = ABC△ 3 2 3+ 3, 2, 45a c B= = = ° sinC 4cos 5ADC∠ = − tan DAC∠ ABC△ 3, 2, 45a c B= = = ° 2 2 2 2 cosb a c ac B= + − 2 9 2 2 3 2 cos45 5b = + − × × ° = 5b = ABC△ sin sin b c B C = 5 2=sin 45 sinC° 5sin .5C = ADC△ 4cos 5ADC∠ = − ADC∠ 180ADC C CAD∠ + ∠ + ∠ = ° C∠ 2 2 5cos 1 sin ,5C C= − = sin 1tan cos 2 CC C = = 因 为 ， 所 以 ， . 从而 . 【点睛】本小题主要考查正弦定理、余弦定理解三角形，考查三角恒等变换，属于中档 题. 17．【2020 年高考天津】在 中，角 所对的边分别为 ．已知 ． （Ⅰ）求角 的大小； （Ⅱ）求 的值； （Ⅲ）求 的值． 【解析】（Ⅰ）在 中，由余弦定理及 ，有 ．又因为 ，所以 ． （Ⅱ）在 中，由正弦定理及 ，可得 ． （Ⅲ）由 及 ，可得 ， 进而 ． 所以， ． 【点晴】本题主要考查正、余弦定理解三角形，以及三角恒等变换在解三角形中的应用， 考查学生的数学运算能力，是一道容易题. 4cos 5ADC∠ = − 2 3sin 1 cos 5ADC ADC∠ = − ∠ = sin 3tan cos 4 ADCADC ADC ∠∠ = = −∠ 3 1 tan( ) 24 2tan tan(180 ) tan( )= = =3 11 tan tan 111 ( )4 2 ADC CADC ADC C ADC C ADC C − +∠ + ∠∠ = ° − ∠ − ∠ = − ∠ + ∠ − −− ∠ × ∠ − − × ABC△ , ,A B C , ,a b c 2 2, 5, 13a b c= = = C sin A πsin(2 )4A+ ABC△ 2 2, 5, 13a b c= = = 2 2 2 2cos 2 2 a b cC ab + −= = (0,π)C ∈ π 4C = ABC△ π , 2 2, 134C a c= = = sin 2 13sin 13 a CA c = = a c< 2 13sin 13A = 2 3 13cos 1 sin 13A A= − = 212 5sin 2 2sin cos ,cos2 2cos 113 13A A A A A= = = − = π π π 12 2 5 2 17 2sin(2 ) sin 2 cos cos2 sin4 4 4 13 2 13 2 26A A A+ = + = × + × = 18．【2020 年高考北京】在 中， ，再从条件①、条件②这两个条件中选择 一个作为己知，求： （Ⅰ）a 的值： （Ⅱ） 和 的面积． 条件①： ； 条件②： ． 注：如果选择条件①和条件②分别解答，按第一个解答计分． 【解析】选择条件①（Ⅰ） （Ⅱ） 由正弦定理得： 选择条件②（Ⅰ） 由正弦定理得： （Ⅱ） 【点睛】本题考查正弦定理、余弦定理，三角形面积公式，考查基本分析求解能力，属 中档题. ABC 11a b+ = sinC ABC 17,cos 7c A= = − 1 9cos ,cos8 16A B= = 17,cos 7c A= = − ， 11a b+ = 2 2 2 2 2 2 12 cos (11 ) 7 2(11 ) 7 ( )7a b c bc A a a a= + − ∴ = − + − − ⋅ ⋅ − 8a∴ = 21 4 3cos (0, ) sin 1 cos7 7A A A Aπ= − ∈ ∴ = − = ， 8 7 3sinsin sin sin 24 3 7 a c CA C C = ∴ = ∴ = 1 1 3sin (11 8) 8 6 32 2 2S ba C= = − × × = 1 9cos ,cos , (0, )8 16A B A B π= = ∈ ， 2 23 7 5 7sin 1 cos ,sin 1 cos8 16A A B B∴ = − = = − = 11 6sin sin 3 7 5 7 8 16 a b a a aA B −= ∴ = ∴ = 3 7 9 5 7 1 7sin sin( ) sin cos sin cos 8 16 16 8 4C A B A B B A= + = + = × + × = 1 1 7 15 7sin (11 6) 62 2 4 4S ba C= = − × × = 19．【2020年高考浙江】在锐角△ABC中，角A，B，C所对的边分别为a，b，C．已知 ． （Ⅰ）求角B的大小； （Ⅱ）求cosA+cosB+cosC的取值范围． 【解析】（Ⅰ）由正弦定理得 ，故 ， 由题意得 . （Ⅱ）由 得 ， 由 是锐角三角形得 . 由 得 . 故 的取值范围是 . 【点睛】解三角形的基本策略：一是利用正弦定理实现“边化角”，二是利用余弦定理实 现“角化边”；求最值也是一种常见类型，主要方法有两类，一是找到边之间的关系，利 用基本不等式求最值，二是转化为关于某个角的函数，利用函数思想求最值. 20．【2020 年新高考全国Ⅰ卷】在① ，② ，③ 这三个条件中任选一 个，补充在下面问题中，若问题中的三角形存在，求 的值；若问题中的三角形不存在， 说明理由． 问题：是否存在 ，它的内角 的对边分别为 ，且 ， ，________? 注：如果选择多个条件分别解答，按第一个解答计分． 【解析】方案一：选条件①． 由 和余弦定理得 ． 由 及正弦定理得 ． 于是 ，由此可得 ． 2 sin 3 0b A a− = 2sin sin 3sinB A A= 3sin 2B = π 3B = πA B C+ + = 2π 3C A= − ABC△ π π( , )6 2A∈ 2π 1 3cos cos( ) cos sin3 2 2C A A A= − = − + 3 1 1 π 1 3 1 3cos cos cos sin cos sin( ) ( , ]2 2 2 6 2 2 2A B C A A A ++ + = + + = + + ∈ cos cos cosA B C+ + 3 1 3( , ]2 2 + 3ac = sin 3c A = 3c b= c ABC△ , ,A B C , ,a b c sin 3sinA B= 6C π= 6C π= 2 2 2 3 2 2 a b c ab + − = sin 3sinA B= 3a b= 2 2 2 2 3 3 22 3 b b c b + − = b c= 由① ，解得 ． 因此，选条件①时问题中的三角形存在，此时 ． 方案二：选条件②． 由 和余弦定理得 ． 由 及正弦定理得 ． 于是 ，由此可得 ， ， ． 由② ，所以 ． 因此，选条件②时问题中的三角形存在，此时 ． 方案三：选条件③． 由 和余弦定理得 ． 由 及正弦定理得 ． 于是 ，由此可得 ． 由③ ，与 矛盾． 因此，选条件③时问题中的三角形不存在． 【点睛】在处理三角形中的边角关系时，一般全部化为角的关系，或全部化为边的关 系．题中若出现边的一次式一般采用到正弦定理，出现边的二次式一般采用到余弦定 理．应用正、余弦定理时，注意公式变式的应用．解决三角形问题时，注意角的限制范 围． 1．【2020·上海高三一模】若不等式 对 上恒成立，则 A． B． C．1 D．2 3ac = 3, 1a b c= = = 1c = 6C π= 2 2 2 3 2 2 a b c ab + − = sin 3sinA B= 3a b= 2 2 2 2 3 3 22 3 b b c b + − = b c= 6B C π= = 2 3A π= sin 3c A = 2 3, 6c b a= = = 2 3c = 6C π= 2 2 2 3 2 2 a b c ab + − = sin 3sinA B= 3a b= 2 2 2 2 3 3 22 3 b b c b + − = b c= 3c b= b c= ( )sin 06x a b x π − − π + ≤   [ ]1,1x∈ − a b+ = 2 3 5 6 【答案】B 【解析】法一： 由题意可知：当 ， ，当 ， ，故当 ， ，当 ， ， 即有 ，故选 B； 法二：由 右图像可得：显然有 ， 故选 B． 【点睛】本题考查双变量不等式中参数的求解问题，通过分段讨论确定交汇点是解题关 键，方法二采用数形结合的方式进一步对方法一作了补充说明，建议将两种方法对比研 究. 2．【2020·广东省高三其他（理）】已知四边形 中， ， ， ， ，E 在 的延长线上，且 ，则 A．1 B．2 C． D． 【答案】A 【解析】在 中，由余弦定理有 ， 1 5,6 6x  ∈ −   sin 06x π π + ≥   1 51, ,16 6x    ∈ − −       sin 06x π π + ≤   1 5,6 6x  ∈ −   0x a b− − ≤ 1 51, ,16 6x    ∈ − −       0x a b− − ≥ 5 106 53 1 61 0 26 a b a a b ba b  − − = =  ⇒ ⇒ + =    =− − − =   sin 6x π π +   5 106 53 1 61 0 26 a b a a b ba b  − − = =  ⇒ ⇒ + =    =− − − =   ABCD //AD BC 30A∠ = ° 2 3AB = 5AD = CB AE BE= AE DB⋅ =  1 2 3 ABD△ 2 2 2 32 cos30 12+25 2 2 3 5 72BD AB AD AB AD= + − ⋅ ⋅ ° = − × × × = ∴ ， 易知 ，又 ， ，故 ， . 故选：A 【点睛】本题考查平面向量数量积的综合运用，涉及了余弦定理的运用，考查运算求解 能力，属于中档题. 3．【2020·安徽省高三三模（理）】函数 的图象大致是 A． B． C． D． 【答案】A 【解析】定义域为 ，定义域关于原点对称， ， 7BD = 30ABE A∠ = ∠ = ° AE BE= 2 3AB = 3 2cos30BE = =° ( ) ( )AE DB BE BA AB AD⋅ = − ⋅ −      BE AB BE AD BA AB BA AD= ⋅ − ⋅ − ⋅ + ⋅        ( )2 2 2 3 cos150 2 5 2 3 5 2 3 cos150 1= × × °+ × + + × × ° = ( ) 3 sin e ex x x xf x − += + R ( ) ( ) ( )3 3sin sin x x x x x x x xf x e e e e− − − + − +− = = −+ + 是奇函数，排除 C，D； 当 时， ，排除 B； 故选：A． 【点睛】本题考查了函数图像的识别，函数奇偶性的判断，属于基础题. 4．【2020·广东省高三其他（理）】在平面直角坐标系中，角 的顶点在坐标原点，其始边与 x 轴的非负半轴重合，终边与单位圆交于点 ，则 ＝ A． B． C． D． 【答案】B 【解析】由定义知 sinα= ， ， 所以 ， 故选：B． 【点睛】该题考查的是有关三角恒等变换的问题，涉及到的知识点有三角函数的定义， 正弦二倍角公式，熟练记忆公式即可解决，属于基础题目. 5．【2020·南昌市八一中学高三三模（理）】已知函数 的图象如图所示， 则函数 的图象可能 A． B． ( )f x x π= ( ) 3 3sin 0e e e ef x π −π π −π π + π π= = >+ + α 3 4,5 5P −   sin 2α 12 25 − 24 25 − 8 5 6 5 − 4 5 3cos 5 α = − 24sin 2 2sin cos 25 α α α= = − sin ( 0)y ax b a= + > log ( )ay x b= − C． D． 【答案】C 【解析】由函数 的图象可得 ， ，故函数 是定义域内的减函数，且过定点 .结合所给 的图像可知只有 C 选项符合题意. 故选：C． 【点睛】本题主要考查由函数 的部分图象求函数的解析式，对数函数的 单调性以及图象特征，属于基础题． 6．【2020·四川省阆中中学高三二模（理）】已知 满足 ，则 A． B． C． D． 【答案】A 【解析】根据两角和差的余弦公式得到 ，因为 ,得到 sin = 或 代入得到结果为 . 故答案为:A． 【点睛】 三角函数求值与化简必会的三种方法 (1)弦切互化法:主要利用公式 tan α= ;形如 ,asin2x+bsin xcos x+ccos2x 等类型可进行弦化切；(2)“1”的灵活代换法:1=sin2θ+cos2θ=(sinθ+cosθ)2-2sinθcosθ=tan 等；(3)和积转换法:利用(sinθ±cosθ)2=1±2sinθcosθ,(sinθ+cosθ)2+(sinθ-cosθ)2=2 的关系进行 sin ( 0)y ax b a= + > 20 1,2 3b a ππ π< < < < 2 13 a∴ < < log ( )ay x b= − (1 ,0)b+ sin( )y A xω ϕ= + α 2 2cos 3 α = cos( )cos( )4 4 α απ π+ − = 7 18 25 18 7 18 − 25 18 − cos cos4 4 π πα α   + − =       ( )( ) 2 21 1cos sin cos sin (cos sin )2 2 α α α α α α− + = − 2 2cos 3 α = α 1 3 1 3 − 7 18 sinα cosα sin cos sin cos a x b x c x d x + + 4 π 变形、转化. 7．【2020·广东省高三一模（理）】已知函数 的图象与 直线 的三个相邻交点的横坐标分别是 2,4,8，则 的单调递减区间 是 A． ， B． ， C． ， D． ， 【答案】D 【解析】由题设可知该函数的最小正周期 ，结合函数的图象可知单调递减 区间是 ，即 ，等价于 ，应选答案 D． 【点睛】解答本题的关键是充分利用题设中的有效信息“函数 的图象与直线 的三个相邻交点的横坐标分别是 2,4,8”．结合图像很容易观察出最小正周期是 ，进而数形结合写出函数的单 调递减区间，从而使得问题获解． 8．【2020·湖北省高三其他（理）】已知函数 的最大值为 3， 的图象与 y 轴 的交点坐标为 ，其相邻两条对称轴间的距离为 ，则 _____． 【答案】 【解析】 ， 因为函数 的最大值为 ，所以 ，所以 ， 由函数 相邻两条对称轴间的距离为 ，可得周期 ， 所以 ，所以 , 所以 ，又 的图象与 y 轴的交点坐标为 ， ( ) ( )sinf x A x= +ω ϕ ( )0, 0A ω> > ( )0y a a A= < < ( )f x [ ]6 ,6 3k kπ π + k ∈Z [ ]6 3,6k kπ − π k ∈Z [ ]6 ,6 3k k + k ∈Z [ ]6 3,6k k− k ∈Z 8 2 6T = − = 2 4 4 8[ 6 , 6 ]( )2 2k k k Z + ++ + ∈ [3 6 ,6 6 ]( )k k k Z+ + ∈ [ ]6 3,6k k− ( ) ( )sinf x A xω ϕ= + ( 0, 0)A ω> > (0 )y a a A= < < 8 2 6T = − = 2( ) cos ( ) 1( 0, 0,0 )2f x A ωx φ A ω φ π= + + > > < < ( )f x (0,2) 2 (1) (2)f f+ = 3 2 1 cos(2 2 )( ) cos ( ) 1 1 cos(2 2 ) 12 2 2 ωx φ A Af x A ωx φ A ωx φ + += + + = ⋅ + = + + + ( )f x 3 1 32 2 A A+ + = 2A = ( )f x 2 4T = 22 2T ω π π= = 4 ω π= ( ) cos( 2 ) 22f x x φ π= + + ( )f x (0,2) 所以 ，所以 ，又 ，所以 ， 所以 ， 所以 . 故答案为： . 【点睛】本题主要考查求三角函数的图象与性质，二倍角的余弦公式，诱导公式，属于 中档题. 9．【2020·福建省福州第一中学高三其他（理）】如图，将地球近似看作球体.设地球表面某 地正午太阳高度角为 ， 为此时太阳直射纬度（当地夏半年取正值，冬半年取负值）， 为该地的纬度值.已知太阳每年直射范围在南北回归线之间，即 . 如果在北京地区（纬度数约为北纬 ）的一幢高为 的楼房北面盖一新楼，要使新楼 一层正午的太阳全年不被前面的楼房遮挡，两楼的距离不应小于_________.（只需列出 式子） 【答案】 【解析】设两楼的距离为 ， 因为 则要使新楼一层正午的太阳全年不被前面的楼房遮挡，需满足 对 恒成立,因此 ，从而两楼的距离不应小于 故答案为： cos2 2 2ϕ + = cos2 0ϕ = 0 2 ϕ π< < = 4 ϕ π ( ) cos( ) 2 sin 22 2 2f x x x π π π= + + = − + (1) (2) sin 2 sin 2 1 2 0 2 32f f π+ = − + − π + = − + − + = 3 θ δ ϕ 23 26 ,23 26δ ′ ′ ∈ −   40 0h 0 tan26 34 h ′ d 90 (40 ) 50 26 34 ,73 26θ δ δ    é ù¢ ¢= - - = + Î ê úë û 0tan h d θ ³ 26 34 ,73 26θ  é ù¢ ¢Î ê úë û 0 min(tan ) h d θ ³ 0tan 26 34 h d  ¢ ³ 0 tan 26 34 hd  ³ ¢ 0 tan26 34 h ′ 0 tan26 34 h ′ 【点睛】本题考查不等式恒成立问题、正切函数单调性，考查基本分析建模能力与转化 求解能力，属中档题. 10．【2020·四川省阆中中学高三二模（理）】在 中，若 ，则 的最小值为_______ 【答案】 【解析】由 ，结合 ， 可得： ， 当且仅当 时， 取得最小值为 . 故答案为： . 【点睛】本题考查余弦定理、利用均值不等式求和的最小值，属综合基础题. 11．【2020·定远县育才学校高三其他（理）】已知函数 是奇函数，将 的图象上所有点 的横坐标伸长到原来的 2 倍（纵坐标不变），所得图象对应的函数为 ．若 的 最小正周期为 ，且 ，则 ______． 【答案】 【解析】函数 是奇函数， 所以 ，代入可得 ， 的图象上所有点的横坐标伸长到原来的 2 倍（纵坐标不变），所得图象对应 的函数为 ． 则 ， 的最小正周期为 ， 则 ，解得 ， ABC ( )2 2 23 5a c b+ = cos B 2 5 ( )2 2 23 5a c b+ = 2 2 2 2a c b accosB+ = + 2 2 2 1 2 2 3 5 5 5 5 b a c c a c acosB ac ac a c a c +  = = = + ≥ × =   a c= cosB 2 5 2 5 ( ) ( )( )sin 0, 0,f x A x Aω ϕ ω ϕ π= + > > < ( )y f x= ( )g x ( )g x 2π 24g π  =   3 8f π  =   2 ( ) ( )( )sin 0, 0,f x A x Aω ϕ ω ϕ= + > > < π ( )0 0f = 0ϕ = ( )y f x= ( )g x ( ) 1sin 2g x A xω =    ( )g x 2π 2 21 2 ω π = π 2ω = 所以 ， 因为 ，代入可得 ， 解得 ， 所以 ， 则 ， 故答案为： . 【点睛】本题考查了正弦函数图像与性质的简单应用，函数图像平移变换及由性质求三 角函数解析式，属于基础题. 12．【2020·六盘山高级中学高三其他（理）】设函数 ， 则下列判断正确的是 A．函数的一条对称轴为 B．函数在区间 内单调递增 C． ，使 D． ，使得函数 在其定义域内为偶函数 【答案】D 【解析】函数 ， 当 时，当 时， 不能使函数取得最值， 所以不是函数的对称轴，A 错； 当 时， ，函数先增后减，B 不正确； 若 ，那么 不成立，所以 C 错； ( ) sing x A x= 24g π  =   2 sin 4A π= 2A = ( ) 2sin 2f x x= 2sin 3 28 823f ×π π   = =       2 2( ) 2cos ( ) sin(2 )8 4f x x x π π= + + + (0,3π)∈x 6x π= 5,2 4 π π     0 (0,3π)x∃ ∈ 0( ) 1f x = − ∃ ∈Ra ( )y f x a= + ( ) 1 cos 2 sin 2 1 2 cos24 4f x x x x π π   = + + + + = +       (0,3π)∈x 6x π= 2 3x π= 5,2 4x π ∈ π   52 , 2x  ∈ π π   ( ) 1f x = − cos2 2x = − 当 时， 函数是偶函数，D 正确， 故选：D． 13．【2020·六盘山高级中学高三其他（理）】已知 中，角 ， ， 所对的边分别 为 ， ， ， ，且满足 . （1）求 的面积 ； （2）若 ，求 的最大值. 【答案】（1） ；（2） . 【解析】（1）在 中， ，∴ ， ∵ ， ∴ ， ∵ ，∴ ， ∴ ， （2）∵ ， ∴ ， ∴ ， ∴ ∴当 时， 取最大值 . 【点睛】本题考查二倍角公式，诱导公式，两角和与差的正弦公式，余弦定理．本题关 键是 ，这样可把 表示为角 的函 数，从而求得最值． 14．【2020·湖北省高三其他（理）】已知 的内角 A，B，C 所对的边分别是 a，b，c， 其面积 S ． 3 2a = π ( ) 1 2 cos2f x a x+ = − ABC△ A B C a b c 2A π≠ ( )sin 2 20cos 0bc A B C+ + = ABC△ S 2 4a S= c b b c + 5 2 2 ABC∆ A B C π+ + = B C A+ = π − ( )sin 2 20cos 0bc A B C+ + = 2 sin cos 20cos 0bc A A A⋅ − = 2A π≠ cos 0A ≠ 1 sin 52S bc A= = 2 4a S= 2 2 2 cos 2 sinb c bc A bc A+ − = 2 2 2 sin 2 cosb c bc A bc A+ = + 2 2 2sin 2cos 2 2 sin 4 c b b c A A Ab c bc + π + = = + = +   4A π= c b b c + 2 2 2 2 22 cos 2 sinb c bc A a bc A+ − = = 2 2c b b c b c bc ++ = A ABC 2 2 2 4 b c a+ −= （1）若 a ，b ，求 cosB． （2）求 sin（A+B）+sinBcosB+cos（B﹣A）的最大值． 【答案】（1） ；（2） . 【解析】（1）因为三角形面积为 S ， 所以 ， 解得 ， 因为 a ，b ， 由正弦定理得： ， 所以 ， 因为 ， 所以 ， 所以 为锐角， 所以 （2）由（1）知 ， 所以 sin（A+B）+sinBcosB+cos（B﹣A）， ， ， ， 6= 2= 30 6 5 2 2 2 21 sin2 4 + −= = b c abc A 2 2 2 sin cos2 b c aA Abc + −= = 4A π= 6= 2= sin sin a b A B = 22sin 62sin 66 × = = =b AB a a b> A B> B 30cos 6 =B 4A π= π π= sin + + sin cos + cos4 4B B B B    −       2 2 2 2sin cos sin cos sin cos2 2 2 2B B B B B B= + + + + ( )2 sin + cos + sin cosB B B B= 令 ， 因为 ， 所以 ， 所以 ， 原式 ， 当 时，原式取得最大值 . 【点睛】本题主要考查三角形面积公式余弦定理、同角三角函数基本关系式，正弦定理， 两角和与差的三角函数以及二次函数的性质，还考查了转化化归的思想和运算求解的能 力，属于中档题. 15．【2020·广东省高三其他（理）】在 中，已知内角 所对的边分别为 ， 向量 ，向量 ，且 ，角 为锐角. （1）求角 的大小； （2）若 ，求 面积的最大值. 【答案】（1） ；（2） . 【解析】（1）解法一：由 得 ， 即 ， 所以 ， 为锐角， ， ， 即 解法二：由 得 ， sin cos 2 sin 4t B B B π = + = +   30, , ,4 4 4B B π π π   ∈ + ∈ π       sin (0,1]4B π + ∈   (0, 2]t ∈ ( )2 2 21 1 1 3= 2 + = + 2 = + 22 2 2 2 2 t tt t t − − − 2, 4t B π= = 5 2 ABC△ , ,A B C , ,a b c ( 3, 2sin )m B= − (cos ,cos2 )n B B= / /m n  B B 2b = ABC△ 3B π= 3 / /m n  3cos2 2sin cosB= B B− sin 2 3 cos2B B= − tan 2 3B = − B 2 (0, )B∴ ∈ π 22 3B π∴ = 3B π= / /m n  3cos2 2sin cosB= B B− 即 所以 即 ， ，即 为锐角， 所以 . （2）解法一： ， 由余弦定理 ， 得 又 代入上式得 ， 当且仅当 时取等号成立. ， 故 的面积最大值为 . 解法二： ， 由正弦定理 ，得 ， 所以 ， ， 由 . 因为 ，则当 即 时， ， sin 2 3 cos2B B= − sin2 3cos2 0B+ B= 2sin 2 03B+ = π     2 3B+ =k π∴ π 6 2 kB= + π π− B 3B π= , 23B b π= = ∴ 2 2 2 cos 2 a c bB ac + −= 2 2 4 0a c ac+ − − = 2 2 2a c ac+ ≥ 4ac ≤ 2a c= = 1 1 3 3sin 32 2 2 4ABCS ac B ac ac∴ = = × = ≤△ ABC 3 , 23B b π= = ∴ 2 sin bR B = 42 3 R= 42 sin sin 3 a R A A= ⋅ = 4 4 22 sin sin sin 33 3 c R C C A π = ⋅ = = −   1 4 3 2sin sin sin2 3 3S ac B A A π = ⋅ = ⋅ −  △ 2 3 3sin 23 6 3= A π − +   726 6 6A π π π− < − < 2 6 2A = π π− = 3A π max 2 3 3 33 3S = + =△ 故 的面积最大值为 . 【点睛】本题主要考查三角恒等变换，考查余弦定理解三角形、利用不等式求最值；正 弦定理解三角形和三角函数的图像和性质，意在考查学生对这些知识的理解掌握水平和 分析推理能力. 16．【2020·宜宾市叙州区第二中学校高三一模（理）】在 中，角 、 、 的对边 分别是 、 、 ，如果 、 、 成等差数列且 ． （1）当 时，求 的面积 ； （2）若 的面积为 ，求 的最大值． 【答案】（1） ；（2） . 【解析】（1）因为 、 、 成等差数列， 则： ，又 ，所以 ， 因为： ， ，（负 值舍）； 的面积 ； （2） ； 即： ，当且仅当 时等号成立； ； 即 的最大值为： ． 【点睛】本题考查正余弦定理的应用，考查三角形面积公式的应用，考查不等式的应用， 考查逻辑思维能力和运算能力，属于常考题. 17．【2020·山东省高三三模】如图，半圆 O 的直径 AB=2，点 C 在 AB 的延长线上，BC=1， 点 P 为半圆上异于 A，B 两点的一个动点，以点 P 为直角顶点作等腰直角 ，且 点 D 与圆心 O 分布在 PC 的两侧，设 ． ABC 3 ABC△ A B C a b c A B C 3b = 4A π= ABC△ S ABC∆ S S 3 3 4 + 3 3 4 A B C 2A+C = B A B C+ + = π 60B = ° 2sin sin b a aB A = ⇒ = 2 2 2 2 21 2 62 cos 3 2 2 2 2 1 02 2b a c ac B c c c c c +∴ = + − ⇒ = + − × ⇒ − − = ⇒ = ABC∴△ 1 1 2 6 3 3 3sin 22 2 2 2 4S ac B + += = × × × = 2 2 2 2 cosb a c ac B= + − 2 23 2a c ac ac ac ac= + − ≥ − = a c= 1 3 3 3sin2 4 4ABCS ac B ac∆∴ = = ≤ S 3 3 4 PCD△ PAC θ∠ = （1）把线段 PC 的长表示为 的函数； （2）求四边形 ACDP 面积的最大值． 【答案】（1） ， ； （2）5 【解析】（1）依题设易知 是以 为直角的直角三角形， 又 ，所以 . 在 ，由余弦定理得， . 所以 ， 定义域为 . （2）四边形 ACDP 面积为 ， 则 θ 29 8cosPC θ= − 0 2 θ θ π< <    APB△ APB∠ 2,AB PAB θ= ∠ = 2cosPA θ= 3,△ 中，PAC AC PAC θ= ∠ = 2 2 2 2 cosPC PA AC PA AC θ= + − ⋅ 2 2 24cos 9 12cos 9 8cosθ θ θ= + − = − 29 8cosPC θ= − 0 2 πθ θ < <    S 21 1= sin2 2△ △APC PCDS S S AP AC PCθ+ = ⋅ ⋅ + ( )21 12cos 3 sin 9 8cos2 2 θ θ θ= ⋅ ⋅ ⋅ + ⋅ − ( )3 1sin 2 5 4cos22 2 θ θ= + ⋅ − 3 5sin 2 2cos22 2 θ θ= − + ( )9 54 sin 24 2 θ ϕ= + − + 其中 为锐角. 因为 所以 . 又因为 ，所以 ， 所以当 时， 取得最大值为 . 所以四边形 ACDP 面积的最大值为 5 . 【点睛】本题通过引进角,利用余弦定理求边长，再将所求面积表示为角 的函数,从而 构建函数,再求函数的最值，还考查了学生的分析能力，运算能力，属于中档题. 18．【2020·天津高三二模】已知函数 （1）求 的最小正周期； （2）讨论 在区间 上的单调性； 【答案】（1） ；（2） 在区间 上单调递增；在区间 上单调递减. 【解析】（1）依题意， 所以 . （2）依题意，令 ， ， 解得 ， 所以 的单调递增区间为 ， . 设 ， ，易知 ， 所以当 时， 在区间 上单调递增； ( )5 5sin 2 ,2 2 θ ϕ= − + 3 4cos ,sin ,5 5 ϕ ϕ ϕ= = 4 3sin 5 2 ，ϕ = < 0 3 ϕ π< < 0 2 θ π< < 23 θ ϕπ− < − < π 2 = 2 θ ϕ π− S 5 5 =52 2 + θ ( ) ( )2 1cos 3sin cos 2f x x x x x= + − ∈R ( )f x ( )f x ,4 4 π π −   π ( )f x ,4 6 π π −   ,6 4 π π     ( ) 2 1 1 cos2 3 1cos 3sin cos sin 2 sin 22 2 2 2 6 xf x x x x x x + π = + − = + − = +   2T ω π= = π 2 2 22 6 2k x k π π π− + π ≤ + ≤ + π k ∈Z 3 6k x k π π− + π ≤ ≤ + π ( )f x ,3 6k k π π − + π + π   k ∈Z ,4 4A π π = −   ,3 6B k k π π = − + π + π   ,4 6A B π π = −   ,4 4x π π ∈ −   ( )f x ,4 6 π π −   在区间 上单调递减. 【点睛】本题考查利用三角恒等变换化简三角函数解析式，以及用公式法求正弦型三角 函数的最小正周期，用整体法求正弦型三角函数的单调区间，属综合中档题. 19．【2020·广东省高三二模（理）】 中，D 为 上的点， 平分 ， ， ， 的面积为 . （1）求 的长； （2）求 . 【答案】（1） （2） 【解析】（1）因为 ， ， 的面积为 ， ∴ ， ∴ ， ∵ ， 平分 ， ∴ ， ∴ ， 在 中，由余弦定理，得 ， ∴ . （2）在 中，由余弦定理，得 ， ∴ ， 因为 平分 ，所以 ， ∴ ,6 4 π π     ABC△ BC AD BAC∠ 5AD = 8AC = ACD△ 10 3 CD sin B 7 3 3 14 5AD = 8AC = ACD 10 3 1 5 8sin 10 32 DAC× × ∠ = 3sin 2DAC∠ = 0 180BAC° < ∠ < ° AD BAC∠ 0 90DAC° < ∠ < ° 60= °∠DAC ACD△ 2 2 2 2 22 cos 5 8 2 5 8 cos60 49CD AD AC AC AD DAC= + − × × × ∠ = + − × × × ° = 7CD = ACD△ 2 2 25 7 8 1cos 2 5 7 7ADC + −∠ = =× × 2 1 4 3sin 1 cos 1 49 7ADC ADC∠ = − ∠ = − = AD BAC∠ 60BAD CAD∠ = ∠ =  ( )sin sin 60 sin cos60 cos sin 60B ADC ADC ADC= ∠ − ° = ∠ − ∠  ， 【点睛】本题考查了余弦定理、三角形内角和定理、三角形的面积公式、两角差的正弦 公式，属于基础题. 20．【2020·四川省泸县第四中学高三二模（理）】△ 的内角 的对边分别为 , 且 ． （1）求角 的大小； （2）若 ,△ 的面积 ,求 的周长． 【答案】（1） ；（2） ． 【解析】（1）∵ ，∴ ． ∴ ， ∴ ， ∴ ， ∴ ， ∴ ． （2）依题意得： ∴ ， ∴ ， ∴ ， ∴ ， ∴ 的周长为 ． 4 3 1 1 3 3 3 7 2 7 2 14 = × − × = ABC , ,A B C , ,a b c ( )sin sin sinC B A B= + − A 7a = ABC 3 3 2S = △ ABC 3A π= 5 7+ A B C+ + = π ( )C A B= π − + sin sin( ) sin sin( )C A B B A B= + = + − sin cos cos sin sin sin cos cos sinA B A B B A B A B⋅ + ⋅ = + ⋅ − 2cos sin sinA B B⋅ = 1cos 2A = 3A π= 2 2 2 1 3 3·sin2 2 2 cos ABCS bc A a b c bc A  = =  = + − △ 2 2 6 13 bc b c =  + = 2 2 2( ) 2 25b c b c bc+ = + + = 5b c+ = 5 7a b c+ + = + ABC∆ 5 7+