2018年上海中考数学试卷

2018年上海中考数学试卷

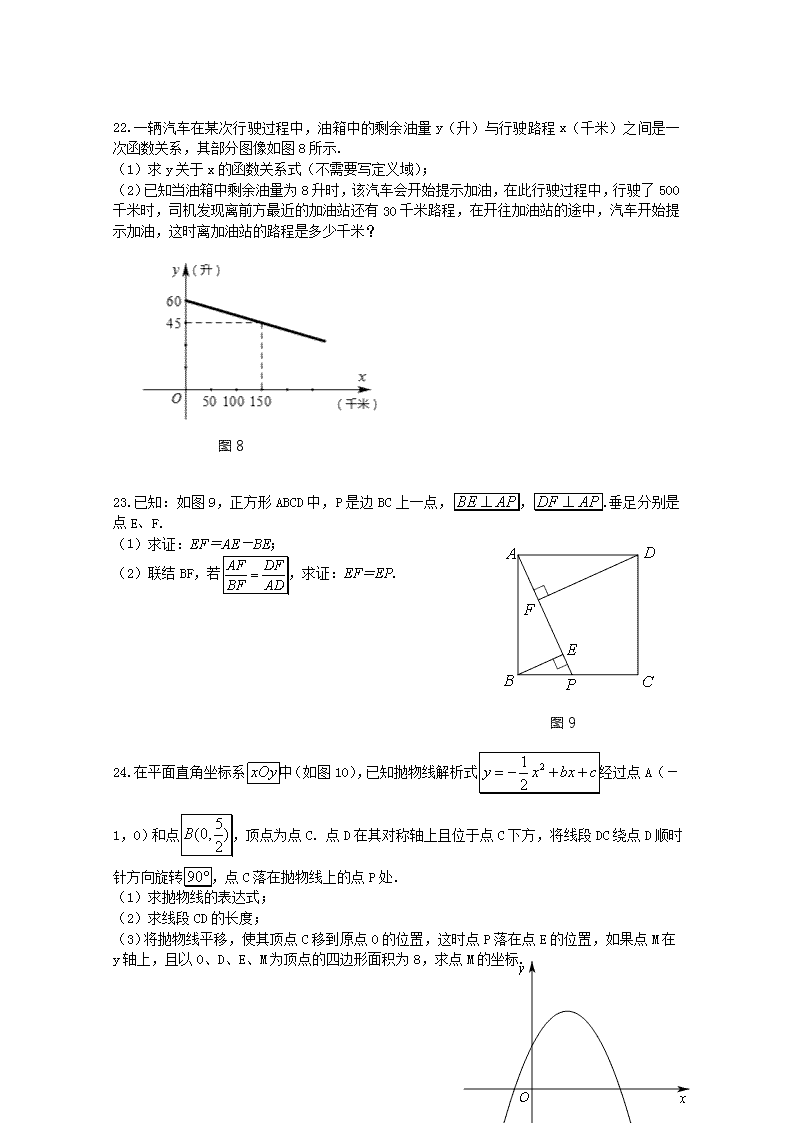
‎2018年上海市初中毕业统一学业考试数学试卷 一、选择题（本大题共6题，每题4分，满分24分）‎ ‎1.计算的结果是（ ）‎ A. 4 B.3 C. D. ‎ ‎2.下列对一元二次方程根的情况的判断，正确的是（ ）‎ A.有两个不相等的实数根 B.有两个相等的实数根 C.有且只一个实数根 D.没有实数根 ‎3.下列对二次函数的图像的描述，正确的是（ ）‎ A.开口向下 B.对称轴是y轴C.经过原点 D.在对称轴右侧部分是下降的 ‎4.据统计，某住宅楼30户居民五月份最后一周每天实行垃圾分类的户数依次是：27，30，29，25，26，28，29.那么这组数据的中位数和众数分别是（ ）‎ A.25和30 B.25和29 C.28和30 D.28和29‎ A. B. C. D. ‎ ‎6.如图1，已知，点A、B在射线OQ上（点A在点O、B之间），半径长为2的与直线OP相切，半径长为3的与相交，那么OB的取值范围是（ ）‎ 图1‎ A. B. C. D. ‎ 二、填空题（本大题共12题，每题4分，满分48分）‎ ‎7. －8的立方根是 .‎ ‎8. 计算：＝ .‎ ‎9.方程组的解是 .‎ ‎10.某商品原价为a元，如果按原价的八折销售，那么售价是 元（用含字母a的代数式表示）.‎ ‎11.已知反比例函数（k是常数，）的图像有一支在第二象限，那么k的取值图2‎ 范围是 .‎ ‎12.某学校学生自主建立了一个学习用品义卖平 台，已知九年级200名学生义卖所得金额分布 直方图如图2所示，那么20－30元这个小组 的组频率是 .‎ ‎13.从这三个数中任选一个数，‎ 选出的这个数是无理数的概率为 .‎ ‎14.如果一次函数（k是常数，）的图像经过点（1，0），那么y的值随着x的增大而 （填“增大”或“减小”）‎ ‎15.如图3，已知平行四边形ABCD，E是边BC的中点，联结DE并延长，与AB的延长线交于点F，设DA＝a，DC＝b，那么向量用向量表示为 .‎ ‎16.通过画出多边形的对角线，可以把多边形内角和问题转化为三角形内角和问题，如果从某个多边形的一个顶点出发的对角线共有2条，那么该多边形的内角和是 度.‎ ‎17.如图4，已知正方形DEFG的顶点D、E在的边BC上，顶点G、F分别在边AB、AC上，如果BC＝4，的面积是6，那么这个正方形的边长是 .‎ 图4‎ 图3‎ 图5‎ 图6‎ ‎18.对于一个位置确定的图形，如果它的所有点都在一个水平放置的矩形内部或边上，且该图形与矩形每条边都至少有一个公共点（如图5），那么这个矩形水平方向的边长称为该图形的宽，铅垂方向的边长称为该矩形的高， 如图6，菱形ABCD的边长为1，边AB水平放置，如果该菱形的高是宽的，那么它的宽的值是 .‎ 三、解答题（共7题，满分78分）‎ ‎19.解不等式组：，并把解集在数轴上表示出来.‎ ‎20.先化简，再求值：，其中.‎ ‎21.如图7，已知中，AB＝BC＝5，.‎ ‎（1）求AC的长；‎ 图7‎ ‎（2）设边BC的垂直平分线与边AB的交点为D，求的值.‎ ‎22.一辆汽车在某次行驶过程中，油箱中的剩余油量y（升）与行驶路程x（千米）之间是一次函数关系，其部分图像如图8所示.‎ ‎（1）求y关于x的函数关系式（不需要写定义域）；‎ ‎（2）已知当油箱中剩余油量为8升时，该汽车会开始提示加油，在此行驶过程中，行驶了500千米时，司机发现离前方最近的加油站还有30千米路程，在开往加油站的途中，汽车开始提示加油，这时离加油站的路程是多少千米？‎ 图8‎ 图9‎ ‎23.已知：如图9，正方形ABCD中，P是边BC上一点，，.垂足分别是点E、F.‎ ‎（1）求证：EF＝AE－BE；‎ ‎（2）联结BF，若，求证：EF＝EP.‎ ‎24.在平面直角坐标系中（如图10），已知抛物线解析式经过点A（－1，0）和点，顶点为点C. 点D在其对称轴上且位于点C下方，将线段DC绕点D顺时针方向旋转，点C落在抛物线上的点P处.‎ ‎（1）求抛物线的表达式；‎ ‎（2）求线段CD的长度；‎ 图10‎ ‎（3）将抛物线平移，使其顶点C移到原点O的位置，这时点P落在点E的位置，如果点M在y轴上，且以O、D、E、M为顶点的四边形面积为8，求点M的坐标.‎ ‎ ‎ ‎25. 已知的直径AB＝2，弦AC与弦BD交于点E，且，垂足为点F.‎ ‎（1）如图11，如果AC＝BD，求弦AC的长；‎ ‎（2）如图12，如果E为弦BD的中点，求的余切值；‎ ‎（3）联结BC、CD、DA，如果BC是的内接正n边形的一边，CD是的内接正(n+4)边形的一边，求的面积.‎ 图12‎ 图11‎ 备用图 ‎2018年上海中考数学试卷参考答案 ‎2018中考数学试卷专家点评 重视数学理解 关注理性思考 着眼学科素养 ‎6月17日下午，2018年上海市初中毕业统一学业考试数学科目顺利开考。市教育考试院邀请了三林中学北校杨正家、虹口区教师进修学院胡军、嘉定区教育学院孙琪斌、青浦区重固中学宋伟倩等专家对本次数学试卷进行了评析。‎ 与会专家表示，2018年上海市初中毕业统一学业考试数学试卷以《2018年上海市初中数学课程终结性评价指南》和《上海市初中数学学科教学基本要求》为依据，试卷结构合理，区分度适切，有效考查了学生的数学核心素养，全卷体现了以下特点：‎ 关注基础 重视通性通法 ‎2018年上海中考数学试卷知识覆盖面广，结构稳定，重视对基础知识、基本技能的考查，部分试题源于教材，没有偏题、怪题，突出了重点知识的考查，符合教学实际。如第19题考查了不等式组的基本解法，第20题考查了分式的基本运算，第21题考查了基本几何计算。‎ 试卷重视基本数学思想方法的考查。如第24题各小题的设计梯度合理，层层递进，由易到难。第(1)题“求这条抛物线的表达式”，考查待定系数法这一基本的数学方法;第(2)题“求线段CD的长”考查数形结合的思想方法;第(3)题“求点M的坐标”，立足图形运动，考查学生的空间观念以及分类讨论的思想。‎ 联系实际 突出数学应用 试卷注重数学知识与现实生活的联系，考查学生在实际生活中分析问题、解决问题的能力。如选择题第4题以居民垃圾分类为素材，要求学生找出相关数据中的中位数和众数;第12题以某校学生自主建立学习用品义卖平台为素材，要求学生根据义卖所得金额的频数分布直方图，求“20-30元这个小组的组频率”;第22题用汽车在行驶过程中油箱用油量和行驶路程之间的函数关系来求解相关问题等，这些试题的背景取材来自现实生活，渗透环保意识，弘扬助人精神，富有亲切感，让学生在解题的同时，感受数学在生活中的广泛运用，体现了学科育人价值。‎ 关注理解 凸显理性思考 试卷注重阅读理解能力、探究性学习能力，引导学生抓住数学本质、数学规律来解决问题。如第25题中，“求弦AC的长”对同圆或等圆中的弦、弧、圆心角三者之间关系的理解是问题解决的关键;“求∠ABD的余切值”需要学生联系基本图形，将所求的余切值转换为相关线段之间的关系，考查了知识间的联系和转换;“求△ACD的面积”需要学生理解正多边形的相关概念，通过数形结合建立方程，运用代数方法解决几何问题。这类试题较好体现了对数学理性思考的关注。‎ 引导教学 着眼核心能力 试卷着眼于学生数学核心能力的培育，如数学表达、运算求解、推理论证、空间想象、数据处理等能力均在试卷中有所体现，对课堂教学起到了较好的引导作用，引导课堂教学关注思维过程与方法，用数学的方式观察、思考、表达、解决所面对的问题。如第23题是一道几何证明题，改编自教材，考查逻辑推理能力，培养思维和表达的严密性。‎