青岛初中数学七年级下册第十二章第二节完全平方公式

青岛初中数学七年级下册第十二章第二节完全平方公式

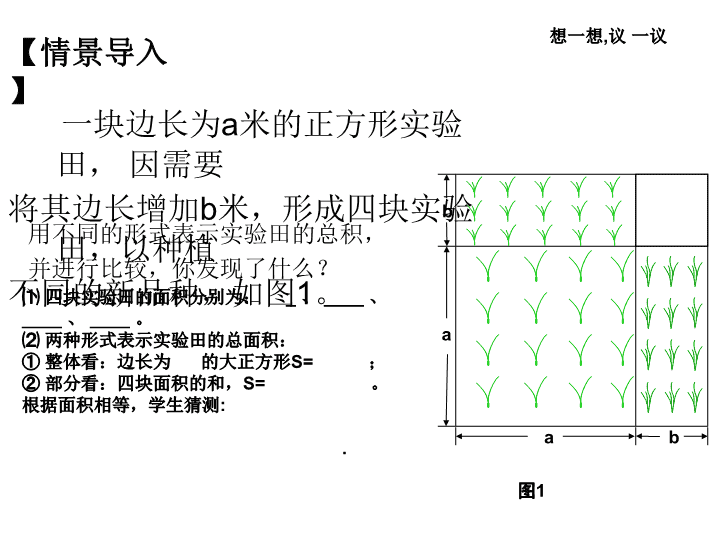
【课前延伸】 § （1） （2a+b）(a+2b)= § (2) (3m-n) (m-2n)= （回顾 多项式乘多项式法则和合并同类项法则） 一块边长为a米的正方形实验 田， 因需要 将其边长增加b米，形成四块实验 田，以种植 不同的新品种，如图1。 用不同的形式表示实验田的总积， 并进行比较，你发现了什么？ 图1 a b a b 【情景导入】 想一想,议 一议 ⑴ 四块实验田的面积分别为： _ 、 ____ 、 ____ 、 ____ 。 ⑵ 两种形式表示实验田的总面积： ① 整体看：边长为 的大正方形S= ； ② 部分看：四块面积的和，S= 。 根据面积相等，学生猜测: . 学习目标 1、会推导完全平方公式，并了解公式的几何 解释 2、能说出完全平方公式的特征，会正确运用 完全平方公式进行简单计算。 3、经历探索完全平方公式的过程，进一步发 展符号感和推理能力，培养学生数学建模 的思想。 学习重点及难点 难点：① 对公式中字母a、b的广泛含义的 理解与正确应用。 ② 正确、灵活地选用公式模型。 重点：体会完全平方公式的发现和推导过程， 熟练掌握完全平方公式的结构特点及公式的 直接运用。 b ba a  2)( ba (a+b)² a² 2a b² 2b ab ab ab2+ + 完全平方和公式： 完全平方公式 的图形理解 1、看一看【课内探究】 a a b b (a-b)²  2)( ba 2a ab 2 22a ab b   a² ab ab ab 2b b²b b 完全平方差公式： 完全平方公式 的图形理解 2、推一推 § ① (a+b) ² =(a+b) (a+b) =a²+ab+ab+b² = a²+2ab+ b² ② (a-b) ² = (a-b) (a-b) =a²-ab-ab+b² = a²-2ab+ b² 3、归一归 § 两数和的平方，等于它们平方的和，加上它们乘积的两倍； § (a+b) ²=a²+2ab+b² § 两数差的平方，等于它们平方的和，减去它们乘积的两倍。 § (a-b) ²=a²-2ab+ b² § 这两个公式统称为完全平方公式 即：两数和(或差)的平方，等于它们的平方 和，加上(或者减去)它们的积的2倍. 公式特点： 4、公式中的字母a，b可以表示数，单项式和 多项式。 1、积为二次三项式； 2、积中两项为两数的平方和； 3、另一项是两数积的2倍，且与乘式中 间的符号相同. 首平方，末平方， 首末两倍中间放 (⑴)(x+y)2=x2 +y2(2)(x -y)2 =x2 -y2 (3) (x -y)2 =x2+2xy +y2 (4) (x+y)2 =x2 +xy +y2 (x +y)2 =x2+2xy +y2 (x -y)2 =x2 -2xy +y2 (x -y)2 =x2 -2xy +y2 (x +y)2 =x2+2xy +y2 4、判一判（正确与错 误） § 例1、利用完全平方公式计算 § 1、(2m-5n) 2 § 2、（-0.5a+0.1b）2 【精讲点拨】 例1 运用完全平方公式计算： 解: (2m-5n)2= =4m2 (1)(2m-5n)2 (2m 2 ) -2×2m×5 n +(5n)2 -20mn +25n2 解: (-0.5a+0.1b)2= =0.25a2 (2)(-0.5a+0.1b)2 (-0.5a) 2 +2×(- 0.5a)×0.1b +(0.1b)2 -0.1ab+0.01b2 § 例2、利用完全平方公式计算 (1) 2012 (2) 1982 (1) 2012 解： 2012= (200+1)2=40000+400+1 =40401 (2) 1982 解： 1982 = (200 –2)2 =40000 -800+4 =39204 例2 运用完全平方公式计算： 【巩固提升】 (1) （x-2y） ² (2) 8.9 ² ( ) ² （x2+1）2 1 2 2 3x y 小试牛刀 【课堂小结】 § 通过这节课的学习你有什么收获？ 【检测反馈】 § 1、填空（每题10分） § ①(2a+b) ² =_____, ②(a-2b) ²=______ § ③(-0.1m+10n) ² =____ ④ 119²= § 2、计算（每题15分） § ①(4x+5y) ²= § ②(-2a ² +b)²= § ③-198²= § ④ (-5b-1) ² = 4a2+4ab+b 2 a2-4ab+4b2 0.01m2-2mn+100n2 14161 16x2+40xy+25y 2 4a2-4a2b+b2 25b2+10b+1 -39204 【课后延伸】 1、解题时常用结论(自己进行探究证明，并 会灵活运用） （1）(-a-b) ² =(a+b) ² (a-b) ² =(b-a) ² （2）a ² + b ² =(a+b) ² - 2ab a ² + b ² =(a-b) ² + 2ab ★2.已知：a-b=5, ab=1 求① a ² +b ²的值. ② (a+b) ²的值 本节课学完了，相信同学一定有不小的收获 吧！ 现在让我们一起放松一下。去享受快乐课间生 活吧！在玩乐的同时不要忘记温习一天所学的功 课和老师布置的作业哦！