2020年上海市中考数学试卷(含解析）

2020年上海市中考数学试卷(含解析）

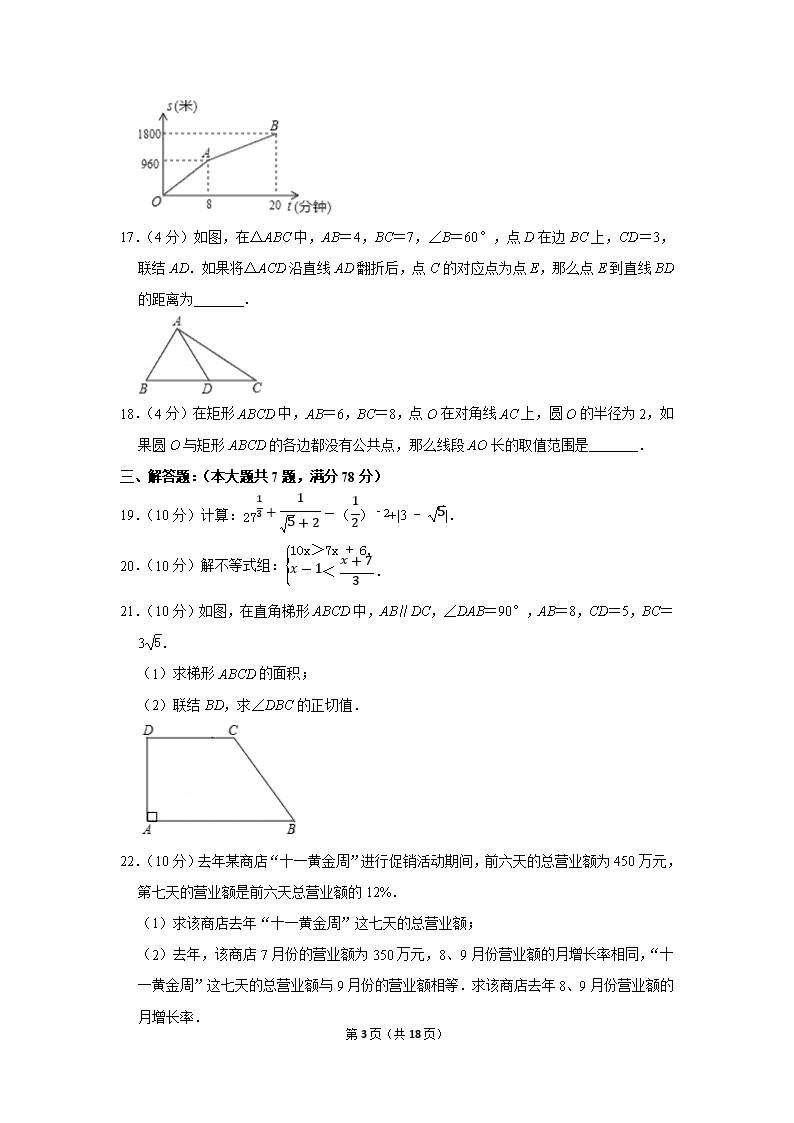
‎2020年上海市中考数学试卷 一、选择题：（本大题共6题，每题4分，满分24分）【下列各题的四个选项中，有且只有一个选项是正确的，选择正确项的代号并填涂在答题纸的相应位置上】‎ ‎1．（4分）下列二次根式中，与‎3‎是同类二次根式的是（　　）‎ A．‎6‎ B．‎9‎ C．‎12‎ D．‎‎18‎ ‎2．（4分）用换元法解方程x+1‎x‎2‎‎+x‎2‎x+1‎=‎2时，若设x+1‎x‎2‎‎=‎y，则原方程可化为关于y的方程是（　　）‎ A．y2﹣2y+1＝0 B．y2+2y+1＝0 C．y2+y+2＝0 D．y2+y﹣2＝0‎ ‎3．（4分）我们经常将调查、收集得来的数据用各类统计图进行整理与表示．下列统计图中，能凸显由数据所表现出来的部分与整体的关系的是（　　）‎ A．条形图 B．扇形图 ‎ C．折线图 D．频数分布直方图 ‎4．（4分）已知反比例函数的图象经过点（2，﹣4），那么这个反比例函数的解析式是（　　）‎ A．y‎=‎‎2‎x B．y‎=-‎‎2‎x C．y‎=‎‎8‎x D．y‎=-‎‎8‎x ‎5．（4分）下列命题中，真命题是（　　）‎ A．对角线互相垂直的梯形是等腰梯形 ‎ B．对角线互相垂直的平行四边形是正方形 ‎ C．对角线平分一组对角的平行四边形是菱形 ‎ D．对角线平分一组对角的梯形是直角梯形 ‎6．（4分）如果存在一条线把一个图形分割成两个部分，使其中一个部分沿某个方向平移后能与另一个部分重合，那么我们把这个图形叫做平移重合图形．下列图形中，平移重合图形是（　　）‎ A．平行四边形 B．等腰梯形 C．正六边形 D．圆 二、填空题：（本大题共12题，每题4分，满分48分）【请将结果直接填入答题纸的相应位置上】‎ ‎7．（4分）计算：2a•3ab＝　 　．‎ ‎8．（4分）已知f（x）‎=‎‎2‎x-1‎，那么f（3）的值是　 　．‎ ‎9．（4分）已知正比例函数y＝kx（k是常数，k≠0）的图象经过第二、四象限，那么y的值 第18页（共18页）‎ 随着x的值增大而　 　．（填“增大”或“减小”）‎ ‎10．（4分）如果关于x的方程x2﹣4x+m＝0有两个相等的实数根，那么m的值是　 　．‎ ‎11．（4分）如果从1，2，3，4，5，6，7，8，9，10这10个数中任意选取一个数，那么取到的数恰好是5的倍数的概率是　 　．‎ ‎12．（4分）如果将抛物线y＝x2向上平移3个单位，那么所得新抛物线的表达式是　 　．‎ ‎13．（4分）为了解某区六年级8400名学生中会游泳的学生人数，随机调查了其中400名学生，结果有150名学生会游泳，那么估计该区会游泳的六年级学生人数约为　 　．‎ ‎14．（4分）《九章算术》中记载了一种测量井深的方法．如图所示，在井口B处立一根垂直于井口的木杆BD，从木杆的顶端D观察井水水岸C，视线DC与井口的直径AB交于点E，如果测得AB＝1.6米，BD＝1米，BE＝0.2米，那么井深AC为　 　米．‎ ‎15．（4分）如图，AC、BD是平行四边形ABCD的对角线，设BC‎→‎‎=‎a‎→‎，CA‎→‎‎=‎b‎→‎，那么向量BD‎→‎用向量a‎→‎、b‎→‎表示为　 　．‎ ‎16．（4分）小明从家步行到学校需走的路程为1800米．图中的折线OAB反映了小明从家步行到学校所走的路程s（米）与时间t（分钟）的函数关系，根据图象提供的信息，当小明从家出发去学校步行15分钟时，到学校还需步行　 　米．‎ 第18页（共18页）‎ ‎17．（4分）如图，在△ABC中，AB＝4，BC＝7，∠B＝60°，点D在边BC上，CD＝3，联结AD．如果将△ACD沿直线AD翻折后，点C的对应点为点E，那么点E到直线BD的距离为　 　．‎ ‎18．（4分）在矩形ABCD中，AB＝6，BC＝8，点O在对角线AC上，圆O的半径为2，如果圆O与矩形ABCD的各边都没有公共点，那么线段AO长的取值范围是　 　．‎ 三、解答题：（本大题共7题，满分78分）‎ ‎19．（10分）计算：‎27‎‎1‎‎3‎‎+‎1‎‎5‎‎+2‎-‎（‎1‎‎2‎）﹣2+|3‎-‎‎5‎|．‎ ‎20．（10分）解不等式组：‎‎10x＞7x+6，‎x-1＜x+7‎‎3‎．‎ ‎21．（10分）如图，在直角梯形ABCD中，AB∥DC，∠DAB＝90°，AB＝8，CD＝5，BC＝3‎5‎．‎ ‎（1）求梯形ABCD的面积；‎ ‎（2）联结BD，求∠DBC的正切值．‎ ‎22．（10分）去年某商店“十一黄金周”进行促销活动期间，前六天的总营业额为450万元，第七天的营业额是前六天总营业额的12%．‎ ‎（1）求该商店去年“十一黄金周”这七天的总营业额；‎ ‎（2）去年，该商店7月份的营业额为350万元，8、9月份营业额的月增长率相同，“十一黄金周”这七天的总营业额与9月份的营业额相等．求该商店去年8、9月份营业额的月增长率．‎ 第18页（共18页）‎ ‎23．（12分）已知：如图，在菱形ABCD中，点E、F分别在边AB、AD上，BE＝DF，CE的延长线交DA的延长线于点G，CF的延长线交BA的延长线于点H．‎ ‎（1）求证：△BEC∽△BCH；‎ ‎（2）如果BE2＝AB•AE，求证：AG＝DF．‎ ‎24．（12分）在平面直角坐标系xOy中，直线y‎=-‎‎1‎‎2‎x+5与x轴、y轴分别交于点A、B（如图）．抛物线y＝ax2+bx（a≠0）经过点A．‎ ‎（1）求线段AB的长；‎ ‎（2）如果抛物线y＝ax2+bx经过线段AB上的另一点C，且BC‎=‎‎5‎，求这条抛物线的表达式；‎ ‎（3）如果抛物线y＝ax2+bx的顶点D位于△AOB内，求a的取值范围．‎ ‎25．（14分）如图，△ABC中，AB＝AC，⊙O是△ABC的外接圆，BO的延长交边AC于点D．‎ ‎（1）求证：∠BAC＝2∠ABD；‎ ‎（2）当△BCD是等腰三角形时，求∠BCD的大小；‎ ‎（3）当AD＝2，CD＝3时，求边BC的长．‎ 第18页（共18页）‎ ‎2020年上海市中考数学试卷 参考答案与试题解析 一、选择题：（本大题共6题，每题4分，满分24分）【下列各题的四个选项中，有且只有一个选项是正确的，选择正确项的代号并填涂在答题纸的相应位置上】‎ ‎1．（4分）下列二次根式中，与‎3‎是同类二次根式的是（　　）‎ A．‎6‎ B．‎9‎ C．‎12‎ D．‎‎18‎ ‎【解答】解：A.‎6‎与‎3‎的被开方数不相同，故不是同类二次根式；‎ B.‎9‎‎=3‎，与‎3‎不是同类二次根式；‎ C.‎12‎‎=2‎‎3‎，与‎3‎被开方数相同，故是同类二次根式；‎ D.‎18‎‎=3‎‎2‎，与‎3‎被开方数不同，故不是同类二次根式．‎ 故选：C．‎ ‎2．（4分）用换元法解方程x+1‎x‎2‎‎+x‎2‎x+1‎=‎2时，若设x+1‎x‎2‎‎=‎y，则原方程可化为关于y的方程是（　　）‎ A．y2﹣2y+1＝0 B．y2+2y+1＝0 C．y2+y+2＝0 D．y2+y﹣2＝0‎ ‎【解答】解：把x+1‎x‎2‎‎=‎y代入原方程得：y‎+‎1‎y=‎2，转化为整式方程为y2﹣2y+1＝0．‎ 故选：A．‎ ‎3．（4分）我们经常将调查、收集得来的数据用各类统计图进行整理与表示．下列统计图中，能凸显由数据所表现出来的部分与整体的关系的是（　　）‎ A．条形图 B．扇形图 ‎ C．折线图 D．频数分布直方图 ‎【解答】解：统计图中，能凸显由数据所表现出来的部分与整体的关系的是扇形图，‎ 故选：B．‎ ‎4．（4分）已知反比例函数的图象经过点（2，﹣4），那么这个反比例函数的解析式是（　　）‎ A．y‎=‎‎2‎x B．y‎=-‎‎2‎x C．y‎=‎‎8‎x D．y‎=-‎‎8‎x ‎【解答】解：设反比例函数解析式为y‎=‎kx，‎ 将（2，﹣4）代入，得：﹣4‎=‎k‎2‎，‎ 解得k＝﹣8，‎ 第18页（共18页）‎ 所以这个反比例函数解析式为y‎=-‎‎8‎x，‎ 故选：D．‎ ‎5．（4分）下列命题中，真命题是（　　）‎ A．对角线互相垂直的梯形是等腰梯形 ‎ B．对角线互相垂直的平行四边形是正方形 ‎ C．对角线平分一组对角的平行四边形是菱形 ‎ D．对角线平分一组对角的梯形是直角梯形 ‎【解答】解：A、对角线相等的梯形是等腰梯形，故错误；‎ B、对角线互相垂直的平行四边形是菱形，故错误；‎ C、正确；‎ D、对角线平分一组对角的梯形是菱形，故错误；‎ 故选：C．‎ ‎6．（4分）如果存在一条线把一个图形分割成两个部分，使其中一个部分沿某个方向平移后能与另一个部分重合，那么我们把这个图形叫做平移重合图形．下列图形中，平移重合图形是（　　）‎ A．平行四边形 B．等腰梯形 C．正六边形 D．圆 ‎【解答】解：如图，平行四边形ABCD中，取BC，AD的中点E，F，连接EF．‎ ‎∵四边形ABEF向右平移可以与四边形EFCD重合，‎ ‎∴平行四边形ABCD是平移重合图形，‎ 故选：A．‎ 二、填空题：（本大题共12题，每题4分，满分48分）【请将结果直接填入答题纸的相应位置上】‎ ‎7．（4分）计算：2a•3ab＝　6a2b　．‎ ‎【解答】解：2a•3ab＝6a2b．‎ 故答案为：6a2b．‎ 第18页（共18页）‎ ‎8．（4分）已知f（x）‎=‎‎2‎x-1‎，那么f（3）的值是　1　．‎ ‎【解答】解：∵f（x）‎=‎‎2‎x-1‎，‎ ‎∴f（3）‎=‎2‎‎3-1‎=‎1，‎ 故答案为：1．‎ ‎9．（4分）已知正比例函数y＝kx（k是常数，k≠0）的图象经过第二、四象限，那么y的值随着x的值增大而　减小　．（填“增大”或“减小”）‎ ‎【解答】解：函数y＝kx（k≠0）的图象经过第二、四象限，那么y的值随x的值增大而减小，‎ 故答案为：减小．‎ ‎10．（4分）如果关于x的方程x2﹣4x+m＝0有两个相等的实数根，那么m的值是　4　．‎ ‎【解答】解：依题意，‎ ‎∵方程x2﹣4x+m＝0有两个相等的实数根，‎ ‎∴△＝b2﹣4ac＝（﹣4）2﹣4m＝0，解得m＝4，‎ 故答案为：4．‎ ‎11．（4分）如果从1，2，3，4，5，6，7，8，9，10这10个数中任意选取一个数，那么取到的数恰好是5的倍数的概率是　‎1‎‎5‎　．‎ ‎【解答】解：∵从1，2，3，4，5，6，7，8，9，10这10个数中任意选取一个数，是5的倍数的有：5，10，‎ ‎∴取到的数恰好是5的倍数的概率是‎2‎‎10‎‎=‎‎1‎‎5‎．‎ 故答案为：‎1‎‎5‎．‎ ‎12．（4分）如果将抛物线y＝x2向上平移3个单位，那么所得新抛物线的表达式是　y＝x2+3　．‎ ‎【解答】解：抛物线y＝x2向上平移3个单位得到y＝x2+3．‎ 故答案为：y＝x2+3．‎ ‎13．（4分）为了解某区六年级8400名学生中会游泳的学生人数，随机调查了其中400名学生，结果有150名学生会游泳，那么估计该区会游泳的六年级学生人数约为　3150名　．‎ 第18页（共18页）‎ ‎【解答】解：8400‎×‎150‎‎400‎=‎3150（名）．‎ 答：估计该区会游泳的六年级学生人数约为3150名．‎ 故答案为：3150名．‎ ‎14．（4分）《九章算术》中记载了一种测量井深的方法．如图所示，在井口B处立一根垂直于井口的木杆BD，从木杆的顶端D观察井水水岸C，视线DC与井口的直径AB交于点E，如果测得AB＝1.6米，BD＝1米，BE＝0.2米，那么井深AC为　7　米．‎ ‎【解答】解：∵BD⊥AB，AC⊥AB，‎ ‎∴BD∥AC，‎ ‎∴△ACE∽△DBE，‎ ‎∴ACBD‎=‎AEBE，‎ ‎∴AC‎1‎‎=‎‎1.4‎‎0.2‎，‎ ‎∴AC＝7（米），‎ 答：井深AC为7米．‎ ‎15．（4分）如图，AC、BD是平行四边形ABCD的对角线，设BC‎→‎‎=‎a‎→‎，CA‎→‎‎=‎b‎→‎，那么向量BD‎→‎用向量a‎→‎、b‎→‎表示为　2a‎→‎‎+‎b‎→‎　．‎ ‎【解答】解：∵四边形ABCD是平行四边形，‎ ‎∴AD＝BC，AD∥BC，AB＝CD，AB∥CD，‎ ‎∴AD‎→‎‎=BC‎→‎=‎a‎→‎，‎ 第18页（共18页）‎ ‎∵CD‎→‎‎=CA‎→‎+AD‎→‎=b‎→‎+‎a‎→‎，‎ ‎∴BA‎→‎‎=CD‎→‎=b‎→‎+‎a‎→‎，‎ ‎∵BD‎→‎‎=BA‎→‎+‎AD‎→‎，‎ ‎∴BD‎→‎‎=b‎→‎+a‎→‎+a‎→‎=‎2a‎→‎‎+‎b‎→‎，‎ 故答案为：2a‎→‎‎+‎b‎→‎．‎ ‎16．（4分）小明从家步行到学校需走的路程为1800米．图中的折线OAB反映了小明从家步行到学校所走的路程s（米）与时间t（分钟）的函数关系，根据图象提供的信息，当小明从家出发去学校步行15分钟时，到学校还需步行　350　米．‎ ‎【解答】解：当8≤t≤20时，设s＝kt+b，‎ 将（8，960）、（20，1800）代入，得：‎ ‎8k+b=960‎‎20k+b=1800‎‎，‎ 解得：k=70‎b=400‎，‎ ‎∴s＝70t+400；‎ 当t＝15时，s＝1450，‎ ‎1800﹣1450＝350，‎ ‎∴当小明从家出发去学校步行15分钟时，到学校还需步行350米，‎ 故答案为：350．‎ ‎17．（4分）如图，在△ABC中，AB＝4，BC＝7，∠B＝60°，点D在边BC上，CD＝3，联结AD．如果将△ACD沿直线AD翻折后，点C的对应点为点E，那么点E到直线BD的距离为　‎3‎‎3‎‎2‎　．‎ 第18页（共18页）‎ ‎【解答】解：如图，过点E作EH⊥BC于H．‎ ‎∵BC＝7，CD＝3，‎ ‎∴BD＝BC﹣CD＝4，‎ ‎∵AB＝4＝BD，∠B＝60°，‎ ‎∴△ABD是等边三角形，‎ ‎∴ADB＝60°，‎ ‎∴∠ADC＝∠ADE＝120°，‎ ‎∴∠EDH＝60°，‎ ‎∵EH⊥BC，‎ ‎∴∠EHD＝90°，‎ ‎∵DE＝DC＝3，‎ ‎∴EH＝DE•sin60°‎=‎‎3‎‎3‎‎2‎，‎ ‎∴E到直线BD的距离为‎3‎‎3‎‎2‎，‎ 故答案为‎3‎‎3‎‎2‎．‎ ‎18．（4分）在矩形ABCD中，AB＝6，BC＝8，点O在对角线AC上，圆O的半径为2，如果圆O与矩形ABCD的各边都没有公共点，那么线段AO长的取值范围是　‎10‎‎3‎‎＜‎AO‎＜‎‎20‎‎3‎　．‎ ‎【解答】解：在矩形ABCD中，∵∠D＝90°，AB＝6，BC＝8，‎ ‎∴AC＝10，‎ 如图1，设⊙O与AD边相切于E，连接OE，‎ 则OE⊥AD，‎ ‎∴OE∥CD，‎ ‎∴△AOE∽△ACD，‎ 第18页（共18页）‎ ‎∴OECD‎=‎AOAC，‎ ‎∴AO‎10‎‎=‎‎2‎‎6‎，‎ ‎∴AO‎=‎‎10‎‎3‎，‎ 如图2，设⊙O与BC边相切于F，连接OF，‎ 则OF⊥BC，‎ ‎∴OF∥AB，‎ ‎∴△COF∽△CAB，‎ ‎∴OCAC‎=‎OFAB，‎ ‎∴OC‎10‎‎=‎‎2‎‎6‎，‎ ‎∴OC‎=‎‎10‎‎3‎，‎ ‎∴AO‎=‎‎20‎‎3‎，‎ ‎∴如果圆O与矩形ABCD的各边都没有公共点，那么线段AO长的取值范围是‎10‎‎3‎‎＜‎AO‎＜‎‎20‎‎3‎，‎ 故答案为：‎10‎‎3‎‎＜‎AO‎＜‎‎20‎‎3‎．‎ 三、解答题：（本大题共7题，满分78分）‎ ‎19．（10分）计算：‎27‎‎1‎‎3‎‎+‎1‎‎5‎‎+2‎-‎（‎1‎‎2‎）﹣2+|3‎-‎‎5‎|．‎ 第18页（共18页）‎ ‎【解答】解：原式＝（33）‎1‎‎3‎‎+‎5‎-‎2﹣4+3‎‎-‎‎5‎ ‎＝3‎+‎5‎-‎2﹣4+3‎‎-‎‎5‎ ‎＝0．‎ ‎20．（10分）解不等式组：‎‎10x＞7x+6，‎x-1＜x+7‎‎3‎．‎ ‎【解答】解：‎10x＞7x+6①‎x-1＜x+7‎‎3‎②‎，‎ 解不等式①得x＞2，‎ 解不等式②得x＜5．‎ 故原不等式组的解集是2＜x＜5．‎ ‎21．（10分）如图，在直角梯形ABCD中，AB∥DC，∠DAB＝90°，AB＝8，CD＝5，BC＝3‎5‎．‎ ‎（1）求梯形ABCD的面积；‎ ‎（2）联结BD，求∠DBC的正切值．‎ ‎【解答】解：（1）过C作CE⊥AB于E，‎ ‎∵AB∥DC，∠DAB＝90°，‎ ‎∴∠D＝90°，‎ ‎∴∠A＝∠D＝∠AEC＝90°，‎ ‎∴四边形ADCE是矩形，‎ ‎∴AD＝CE，AE＝CD＝5，‎ ‎∴BE＝AB﹣AE＝3，‎ ‎∵BC＝3‎5‎，‎ ‎∴CE‎=BC‎2‎-BE‎2‎=‎6，‎ ‎∴梯形ABCD的面积‎=‎1‎‎2‎×‎（5+8）×6＝39；‎ ‎（2）过C作CH⊥BD于H，‎ 第18页（共18页）‎ ‎∵CD∥AB，‎ ‎∴∠CDB＝∠ABD，‎ ‎∵∠CHD＝∠A＝90°，‎ ‎∴△CDH∽△DBA，‎ ‎∴CHAD‎=‎CDBD，‎ ‎∵BD‎=AB‎2‎+AD‎2‎=‎8‎‎2‎‎+‎‎6‎‎2‎=‎10，‎ ‎∴CH‎6‎‎=‎‎5‎‎10‎，‎ ‎∴CH＝3，‎ ‎∴BH‎=BC‎2‎-CH‎2‎=‎(3‎5‎‎)‎‎2‎-‎‎3‎‎2‎=‎6，‎ ‎∴∠DBC的正切值‎=CHBH=‎3‎‎6‎=‎‎1‎‎2‎．‎ ‎22．（10分）去年某商店“十一黄金周”进行促销活动期间，前六天的总营业额为450万元，第七天的营业额是前六天总营业额的12%．‎ ‎（1）求该商店去年“十一黄金周”这七天的总营业额；‎ ‎（2）去年，该商店7月份的营业额为350万元，8、9月份营业额的月增长率相同，“十一黄金周”这七天的总营业额与9月份的营业额相等．求该商店去年8、9月份营业额的月增长率．‎ ‎【解答】解：（1）450+450×12%＝504（万元）．‎ 答：该商店去年“十一黄金周”这七天的总营业额为504万元．‎ ‎（2）设该商店去年8、9月份营业额的月增长率为x，‎ 依题意，得：350（1+x）2＝504，‎ 解得：x1＝0.2＝20%，x2＝﹣2.2（不合题意，舍去）．‎ 答：该商店去年8、9月份营业额的月增长率为20%．‎ ‎23．（12分）已知：如图，在菱形ABCD中，点E、F分别在边AB、AD上，BE＝DF，CE的延长线交DA的延长线于点G，CF的延长线交BA的延长线于点H．‎ ‎（1）求证：△BEC∽△BCH；‎ 第18页（共18页）‎ ‎（2）如果BE2＝AB•AE，求证：AG＝DF．‎ ‎【解答】（1）证明：∵四边形ABCD是菱形，‎ ‎∴CD＝CB，∠D＝∠B，CD∥AB，‎ ‎∵DF＝BE，‎ ‎∴△CDF≌CBE（SAS），‎ ‎∴∠DCF＝∠BCE，‎ ‎∵CD∥BH，‎ ‎∴∠H＝∠DCF，‎ ‎∴∠BCE＝∠H，‎ ‎∵∠B＝∠B，‎ ‎∴△BEC∽△BCH．‎ ‎（2）证明：∵BE2＝AB•AE，‎ ‎∴BEAB‎=‎AEEB，‎ ‎∵AG∥BC，‎ ‎∴AEBE‎=‎AGBC，‎ ‎∴BEAB‎=‎AGBC，‎ ‎∵DF＝BE，BC＝AB，‎ ‎∴BE＝AG＝DF，‎ 即AG＝DF．‎ ‎24．（12分）在平面直角坐标系xOy中，直线y‎=-‎‎1‎‎2‎x+5与x轴、y轴分别交于点A、B（如图）．抛物线y＝ax2+bx（a≠0）经过点A．‎ ‎（1）求线段AB的长；‎ ‎（2）如果抛物线y＝ax2+bx经过线段AB上的另一点C，且BC‎=‎‎5‎ 第18页（共18页）‎ ‎，求这条抛物线的表达式；‎ ‎（3）如果抛物线y＝ax2+bx的顶点D位于△AOB内，求a的取值范围．‎ ‎【解答】解：（1）针对于直线y‎=-‎‎1‎‎2‎x+5，‎ 令x＝0，y＝5，‎ ‎∴B（0，5），‎ 令y＝0，则‎-‎‎1‎‎2‎x+5＝0，‎ ‎∴x＝10，‎ ‎∴A（10，0），‎ ‎∴AB‎=‎5‎‎2‎‎+1‎‎0‎‎2‎=‎5‎5‎；‎ ‎（2）设点C（m，‎-‎‎1‎‎2‎m+5），‎ ‎∵B（0，5），‎ ‎∴BC‎=m‎2‎‎+(-‎1‎‎2‎m+5-5‎‎)‎‎2‎=‎‎5‎‎2‎|m|，‎ ‎∵BC‎=‎‎5‎，‎ ‎∴‎5‎‎2‎|m|‎=‎‎5‎，‎ ‎∴m＝±2，‎ ‎∵点C在线段AB上，‎ ‎∴m＝2，‎ ‎∴C（2，4），‎ 将点A（10，0），C（2，4）代入抛物线y＝ax2+bx（a≠0）中，得‎100a+10b=0‎‎4a+2b=4‎，‎ ‎∴a=-‎‎1‎‎4‎b=‎‎5‎‎2‎，‎ 第18页（共18页）‎ ‎∴抛物线y‎=-‎‎1‎‎4‎x2‎+‎‎5‎‎2‎x；‎ ‎（3）∵点A（10，0）在抛物线y＝ax2+bx中，得100a+10b＝0，‎ ‎∴b＝﹣10a，‎ ‎∴抛物线的解析式为y＝ax2﹣10ax＝a（x﹣5）2﹣25a，‎ ‎∴抛物线的顶点D坐标为（5，﹣25a），‎ 将x＝5代入y‎=-‎‎1‎‎2‎x+5中，得y‎=-‎1‎‎2‎×‎5+5‎=‎‎5‎‎2‎，‎ ‎∵顶点D位于△AOB内，‎ ‎∴0＜﹣25a‎＜‎‎5‎‎2‎，‎ ‎∴‎-‎1‎‎10‎＜‎a＜0；‎ ‎25．（14分）如图，△ABC中，AB＝AC，⊙O是△ABC的外接圆，BO的延长交边AC于点D．‎ ‎（1）求证：∠BAC＝2∠ABD；‎ ‎（2）当△BCD是等腰三角形时，求∠BCD的大小；‎ ‎（3）当AD＝2，CD＝3时，求边BC的长．‎ ‎【解答】（1）证明：连接OA．‎ ‎∵AB＝AC，‎ ‎∴AB‎=‎AC，‎ 第18页（共18页）‎ ‎∴OA⊥BC，‎ ‎∴∠BAO＝∠CAO，‎ ‎∵OA＝OB，‎ ‎∴∠ABD＝∠BAO，‎ ‎∴∠BAC＝2∠BAD．‎ ‎（2）解：如图2中，延长AO交BC于H．‎ ‎①若BD＝CB，则∠C＝∠BDC＝∠ABD+∠BAC＝3∠ABD，‎ ‎∵AB＝AC，‎ ‎∴∠ABC＝∠C，‎ ‎∴∠DBC＝2∠ABD，‎ ‎∵∠DBC+∠C+∠BDC＝180°，‎ ‎∴8∠ABD＝180°，‎ ‎∴∠C＝3∠ABD＝67.5°．‎ ‎②若CD＝CB，则∠CBD＝∠CDB＝3∠ABD，‎ ‎∴∠C＝4∠ABD，‎ ‎∵∠DBC+∠C+∠CDB＝180°，‎ ‎∴10∠ABD＝180°，‎ ‎∴∠BCD＝4∠ABD＝72°．‎ ‎③若DB＝DC，则D与A重合，这种情形不存在．‎ 综上所述，∠C的值为67.5°或72°．‎ ‎（3）如图3中，作AE∥BC交BD的延长线于E．‎ 第18页（共18页）‎ 则AEBC‎=ADDC=‎‎2‎‎3‎，‎ ‎∴AOOH‎=EBH=‎‎4‎‎3‎，设OB＝OA＝4a，OH＝3a，‎ ‎∵BH2＝AB2﹣AH2＝OB2﹣OH2，‎ ‎∴25﹣49a2＝16a2﹣9a2，‎ ‎∴a2‎=‎‎25‎‎56‎，‎ ‎∴BH‎=‎‎5‎‎2‎‎4‎，‎ ‎∴BC＝2BH‎=‎‎5‎‎2‎‎2‎．‎ 第18页（共18页）‎