- 2021-04-14 发布 |
- 37.5 KB |
- 16页

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
七年级上数学课件- 3-1-2 等式的性质 课件(共16张PPT)_人教新课标
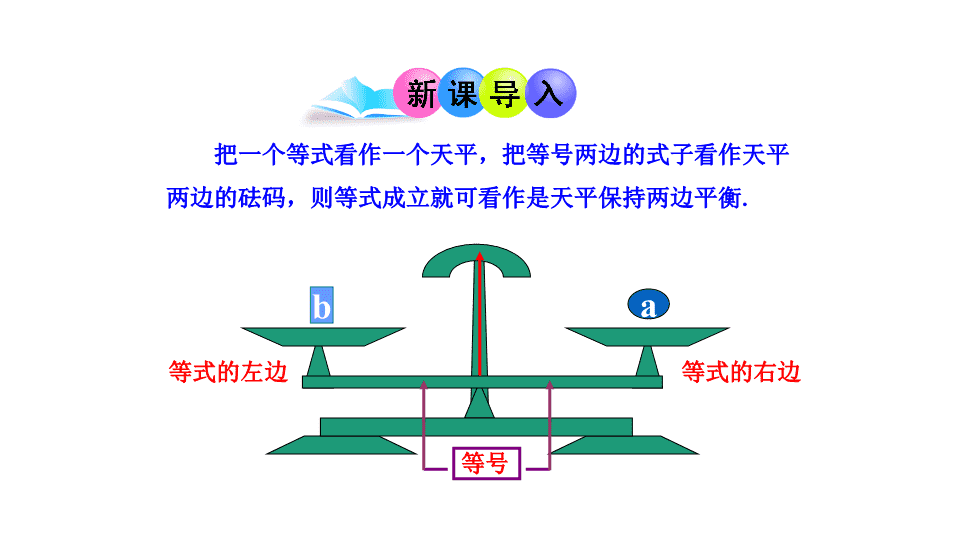
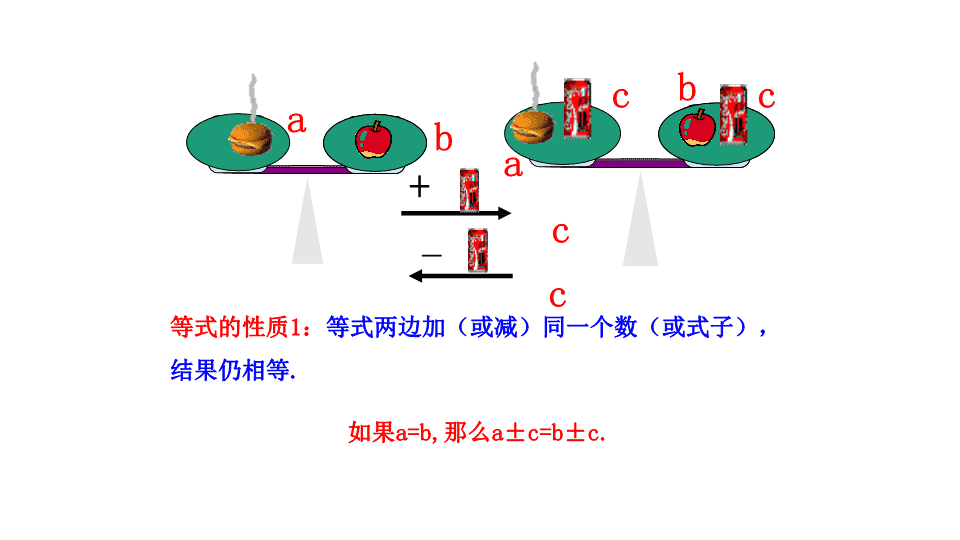
3.1.2 等式的性质 b a 把一个等式看作一个天平,把等号两边的式子看作天平 两边的砝码,则等式成立就可看作是天平保持两边平衡. 等式的左边 等式的右边 等号 + — 等式的性质1:等式两边加(或减)同一个数(或式子), 结果仍相等. 如果a=b,那么a±c=b±c. c a b a b c cc 等式的性质2:等式两边乘同一个数,或除以同一个不为 0的数,结果仍相等. ×3 ÷3 ? ? 如果a=b,那么ac=bc. 如果a=b(c≠0),那么 a aa a bb bb a b.c c a b a c b c. 如果 ,那么 【等式性质2】 a b ac bc. 如果 ,那么 a ba b c 0 , .c c 如果 那么 【等式性质1】 注 意 1.等式两边都要参加运算,并且是作同一种运算. 2.等式两边加或减,乘或除以的数一定是同一个数 或同一个式子. 3.等式两边不能都除以0,即0不能作除数或分母. 若x=y,则下列等式是否成立,若成立,请指明依据等 式的哪条性质?若不成立,请说明理由. (1)x+ 5=y+ 5 (2)x - a = y - a (3)(5-a)x=(5-a)y (4) x y 5 a 5 a 成立,等式性质1 成立,等式性质1 成立,等式性质2 不一定成立,当a=5时等式两边都没 有意义. 思考 1.在下面的括号内填上适当的数或者代数式 xxx xx 2823 823 (2)∵ ∴ xxx xx 9989910 98910(3)∵ ∴ x2 x9 9 4662 462 x x (1)∵ ∴ 6 例1 利用等式的性质解下列方程: (1)x+7=26 (2)3x=2x-4 解:给等式两边同时减7, 得 x+7-7=26-7, 于是 x=19 . 解:给等式两边减同时 减2x,得 3x-2x=2x-2x-4, 于是 x=-4. 1. 解方程: (1) x-3=-5 (2) -5x=4-6x 7 23 x x 15 5 ( ) x=-2 x=4 x=-1 例2 解方程:-4x+8=-5x-1. 解:给等式两边同时减8,得 -4x+8-8=-5x-1-8, -4x=-5x-9, 给等式两边同时加5x,得 -4x+5x=-5x+5x-9, x=-9. 例2 解方程:-4x+8=-5x -1 方程的解是否正确可以检验. 例如:把x=-9代入方程: 左边=-4×(-9)+8=44; 右边=-5×(-9)-1=44. 左边=右边 所以x=-9是方程-4x+8=-5x -1 的解. 2.解方程并检验:-6x+3=2-7x. 解:两边减3,得 -6x=-7x-1 两边加7x,得 x=-1 检验:把x=-1代入方程: 左边=-6×(-1)+3=9; 右边=2-7×(-1)=9. 左边=右边, 所以x=-1是原方程的解. 1.填空,并在括号内注明利用了等式的哪条性 质. (1)如果5+x=4,那么x=____( ) (2)如果-2x=6,那么x=____ ( ) 2.已知m+a=n+b,根据等式的性质变形为m=n, 那么a、b必须符合的条件是( ) A.a=-b B. -a=b C.a=b D.a,b可以是任意 数 -1 等式的性质1 -3 等式的性质2 C 3.如果a=b, 且 则c应满足的条件是_________. 4.解方程 (1)4x - 2 = 2 (2) x + 2 = 6 a b c c 1 2 c≠0 x=1 x=8 5.观察下列变形,并回答问题: 3a+b-2 =2a+b-2 3a+b=2a+b 第一步 3a=2a 第二步 3=2 第三步 上述变形是否正确?若不正确,请指明错在哪一步?原 因是什么?怎么改正? 解:不正确.错在第三步,两边同除以a时,不能保证a不等 于0. 改正:两边同时减2a,得a=0. 本节课我们学习了: 1.等式的性质,并运用性质进行等式变形. 2.运用等式的性质解简单的方程. 3.对方程的解进行检验.查看更多