2020九年级数学下册 第26章 二次函数 26

2020九年级数学下册 第26章 二次函数 26

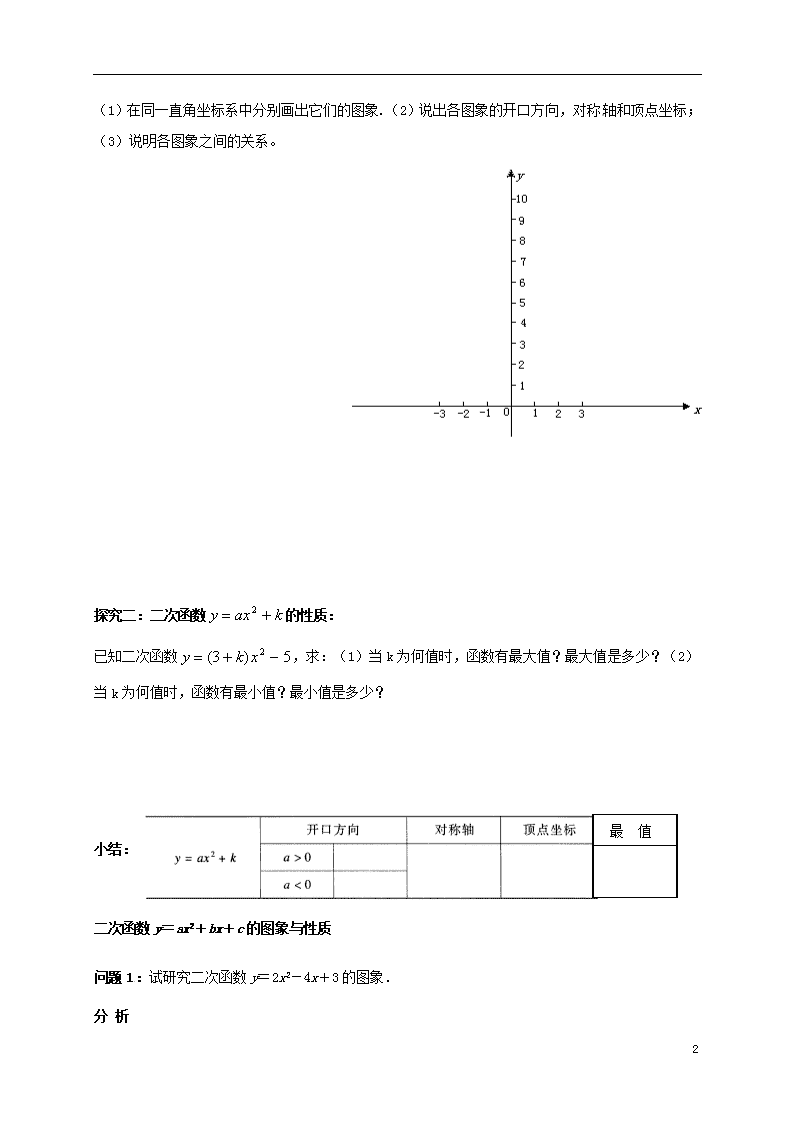
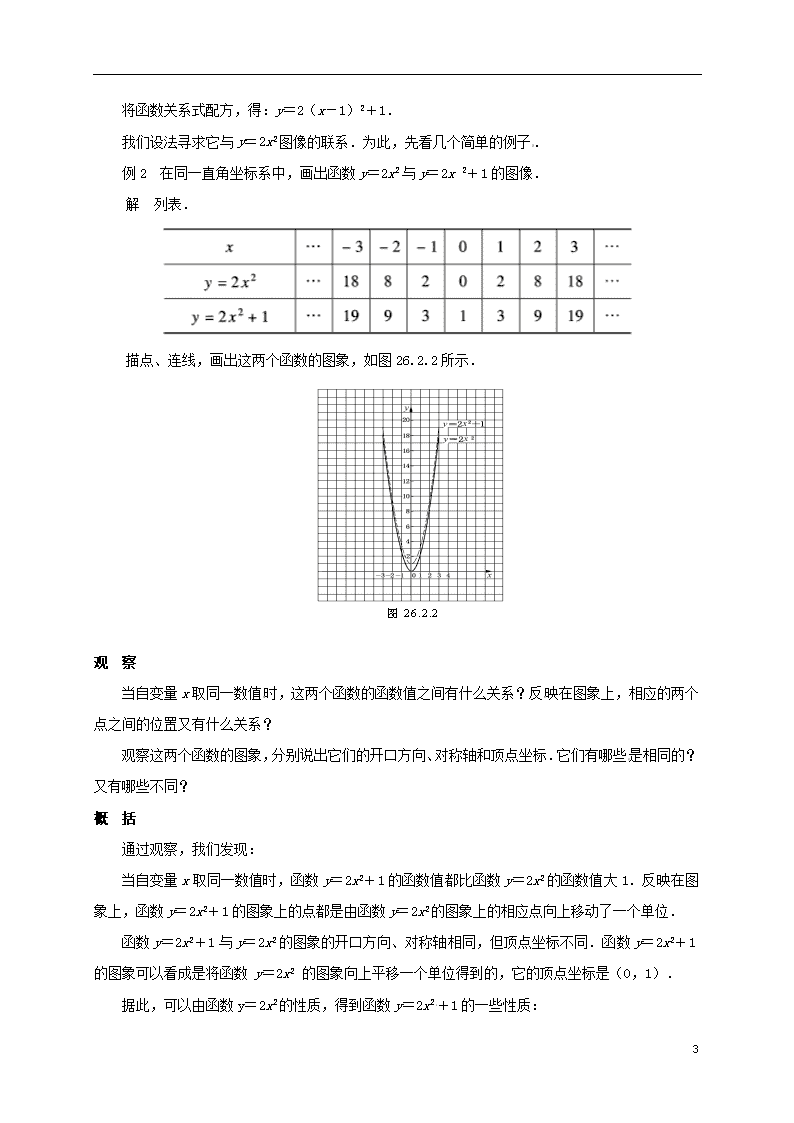
导 学 案 装 订 线 ‎ ‎26.2.2二次函数的图象（2）‎ ‎【学习目标】 ‎ ‎1.会用描点法画出二次函数+k的图象；‎ ‎2.探究抛物线与之间的位置关系。‎ ‎3.体验抛物线平移的过程，形成良好的思维方法。‎ ‎【重点】二次函数的图象和性质 ‎【难点】理解抛物线与之间的位置关系。‎ ‎【使用说明与学法指导】‎ 先预习P3—P4内容，勾画课文中的重点，然后独立完成导学案，疑惑随时记录在课本或预习案上，准备课上讨论质疑；‎ 预 习 案 一、预习导学：‎ ‎1. 二次函数的图象与的图象有什么关系？‎ ‎2.已知二次函数的图象如图所示，则、k的符号分别为 ‎ ‎【预习自测】‎ ‎1.抛物线y＝2x2向上平移3个单位,就得到抛物线___________;‎ 抛物线y＝2x2向下平移4个单位,就得到抛物线__________________.‎ 因此,把抛物线y＝ax2向上平移k(k＞0)个单位,就得到抛物线_______________;‎ 把抛物线y＝ax2向下平移m(m＞0)个单位,就得到抛物线_______________.‎ ‎2.抛物线y＝－3x2与y＝－3x2＋1是通过平移得到的,从而它们的形状__________,‎ 由此可得二次函数y＝ax2与y＝ax2＋k的形状__________________.‎ 二、我的疑惑 ‎ ‎ 合作探究 探究一：二次函数的图象：已知二次函数、、。‎ 4‎ ‎（1）在同一直角坐标系中分别画出它们的图象.（2）说出各图象的开口方向，对称轴和顶点坐标；（3）说明各图象之间的关系。‎ 探究二：二次函数的性质：‎ 已知二次函数，求：（1）当k为何值时，函数有最大值？最大值是多少？（2）当k为何值时，函数有最小值？最小值是多少？‎ 最 值 小结：‎ 二次函数y＝ax2＋bx＋c的图象与性质 问题1：试研究二次函数y＝2x2－4x＋3的图象．‎ 分 析 4‎ 将函数关系式配方，得：y＝2（x－1）2＋1．‎ 我们设法寻求它与y＝2x2图像的联系．为此，先看几个简单的例子．‎ 例2　在同一直角坐标系中，画出函数y＝2x2与y＝2x 2＋1的图像．‎ 解　列表．‎ 描点、连线，画出这两个函数的图象，如图26.2.2所示．‎ 观　察 当自变量x取同一数值时，这两个函数的函数值之间有什么关系？反映在图象上，相应的两个点之间的位置又有什么关系？‎ 观察这两个函数的图象，分别说出它们的开口方向、对称轴和顶点坐标．它们有哪些是相同的？又有哪些不同？‎ 概　括 通过观察，我们发现：‎ 当自变量x取同一数值时，函数y＝2x2＋1的函数值都比函数y＝2x2的函数值大1．反映在图象上，函数y＝2x2＋1的图象上的点都是由函数y＝2x2的图象上的相应点向上移动了一个单位．‎ 函数y＝2x2＋1与y＝2x2的图象的开口方向、对称轴相同，但顶点坐标不同．函数y＝2x2＋1的图象可以看成是将函数 y＝2x2 的图象向上平移一个单位得到的，它的顶点坐标是（0，1）．‎ 据此，可以由函数y＝2x2的性质，得到函数y＝2x2＋1的一些性质：‎ 4‎ 当x_____时，函数值y随x的增大而减小；当x______时，函数值y随x的增大而增大；当x_____时，函数取得最____值，最____值y＝______．‎ 做一做 先在同一直角坐标系中画出函数y＝2x2－2与函数y＝2x2的图象，再作比较，说说它们有什么联系和区别？说出y＝2x2－2的图象的开口方向、对称轴和顶点坐标，并讨论这个函数的性质．‎ 思 考 在同一直角坐标系中，函数y＝－x2＋2的图象与函数y＝－x2的图象有什么关系？你能说出函数y＝－x2＋2的图象的开口方向、对称轴和顶点坐标吗？这个函数有哪些性质？‎ 练 习 ‎1.已知函数y＝－x2、y＝－x2＋2和y＝－x2－2．‎ 1. 分别画出它们的图象；‎ 2. 说出各个图象的开口方向、对称轴和顶点坐标；‎ 3. 试说出函数y＝－x2＋4的图象的开口方向、对称轴和顶点坐标．‎ ‎2.根据上题的结果，试说明：分别通过怎样的平移，可以由抛物线y＝－x2 得到抛物线y＝－x2＋2和y＝－x2－2？如果要得到抛物线y＝－x2＋4，应将抛物线y＝－x2作怎样的平移？‎ ‎3.试说出函数y＝ax2＋k（a、k是常数，a≠0）的图象的开口方向、对称轴和顶点坐标，并填写下表． ‎ 4‎