- 2021-04-14 发布 |
- 37.5 KB |
- 16页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2019年云南省初中学业水平考试数学试题卷
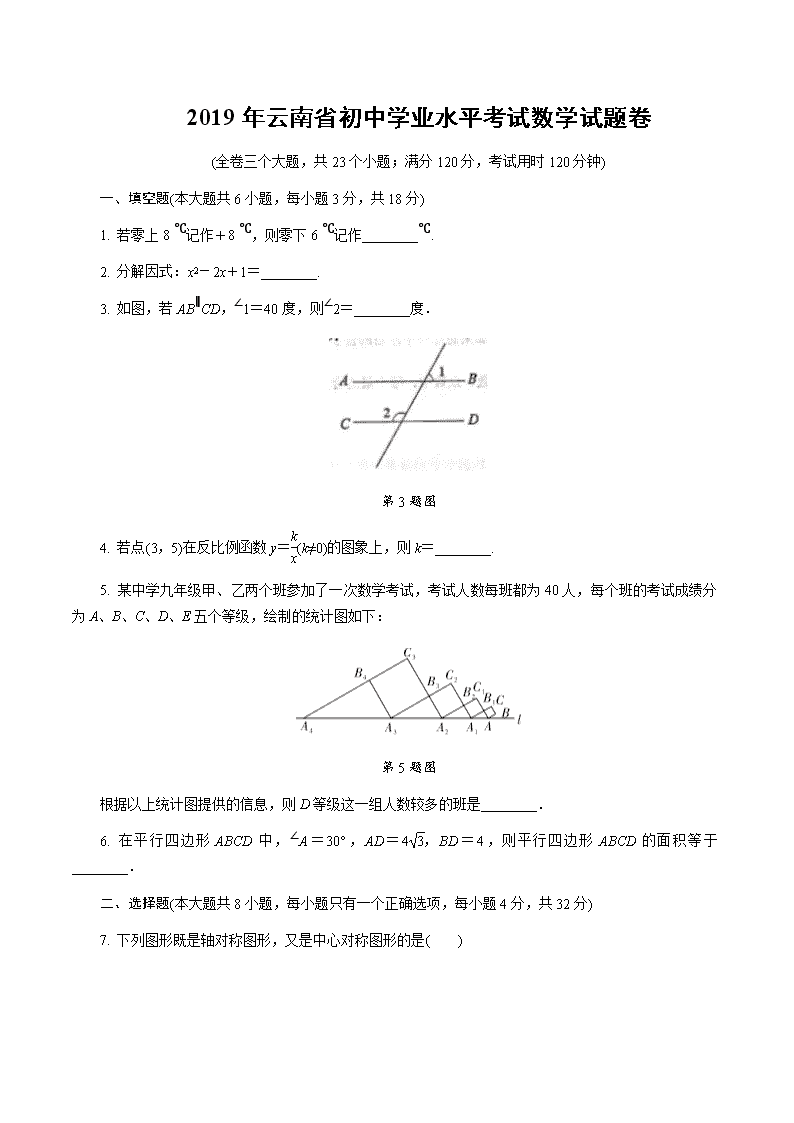
2019年云南省初中学业水平考试数学试题卷 (全卷三个大题,共23个小题;满分120分,考试用时120分钟) 一、 填空题(本大题共6小题,每小题3分,共18分) 1. 若零上8 ℃记作+8 ℃,则零下6 ℃记作________℃. 2. 分解因式:x2-2x+1=________. 3. 如图,若AB∥CD,∠1=40度,则∠2=________度. 第3题图 4. 若点(3,5)在反比例函数y=(k≠0)的图象上,则k=________. 5. 某中学九年级甲、乙两个班参加了一次数学考试,考试人数每班都为40人,每个班的考试成绩分为A、B、C、D、E五个等级,绘制的统计图如下: 第5题图 根据以上统计图提供的信息,则D等级这一组人数较多的班是________. 6. 在平行四边形ABCD中,∠A=30°,AD=4,BD=4,则平行四边形ABCD的面积等于________. 二、选择题(本大题共8小题,每小题只有一个正确选项,每小题4分,共32分) 7. 下列图形既是轴对称图形,又是中心对称图形的是( ) 8. 2019年“五一”期间,某景点接待海内外游客共688000人次,688000这个数用科学记数法表示为( ) A. 68.8×104 B. 0.688×106 C. 6.88×105 D. 6.88×106 9. 一个十二边形的内角和等于( ) A. 2160° B. 2080° C. 1980° D. 1800° 10. 要使有意义,则x的取值范围为( ) A. x≤0 B. x≥-1 C. x≥0 D. x≤-1 11. 一个圆锥的侧面展开图是半径为8的半圆,则该圆锥的全面积是( ) A. 48π B. 45π C. 36π D. 32π 12. 按一定规律排列的单项式:x3,-x5,x7,-x9,x11,…,第n个单项式是( ) A. (-1)n-1x2n-1 B. (-1)nx2n-1 C. (-1)n-1x2n+1 D. (-1)nx2n+1 13. 如图,△ABC的内切圆⊙O与BC、CA、AB分别相切于点D、E、F,且AB=5,BC=13,CA=12,则阴影部分(即四边形AEOF)的面积是( ) A. 4 B. 6.25 C. 7.5 D. 9 第13题图 14. 若关于x的不等式组的解集为x>a,则a的取值范围是( ) A. a<2 B. a≤2 C. a>2 D. a≥2 三、解答题(本大题共9小题,共70分) 15. (本小题6分)计算:32+(π-5)0-+(-1)-1. 16. (本小题6分)如图,AB=AD,CB=CD. 求证:∠B=∠D. 第16题图 17. (本小题8分)某公司销售部有营业员15人,该公司为了调动营业员的积极性,决定实行目标管理,根据目标完成的情况对营业员进行适当的奖励,为了确定一个适当的月销售目标,公司有关部门统计了这15人某月的销售量,如下表所示: 月销售量/件数 1770 480 220 180 120 90 人数 1 1 3 3 3 4 (1)直接写出这15名营业员该月销售量数据的平均数、中位数、众数; (2)如果想让一半左右的营业员都能达到月销售目标,你认为(1)中的平均数、中位数、众数中,哪个最适合作为月销售目标?请说明理由. 18. (本小题6分)为进一步营造扫黑除恶专项斗争的浓厚宣传氛围,推进平安校园建设,甲、乙两所学校各租用一辆大巴车组织部分师生,分别从距目的地240千米和270千米的两地同时出发,前往“研学教育”基地开展扫黑除恶教育活动.已知乙校师生所乘大巴车的平均速度是甲校师生所乘大巴车的平均速度的1.5倍,甲校师生比乙校师生晚1小时到达目的地,分别求甲、乙两所学校师生所乘大巴车的平均速度. 19. (本小题7分)甲、乙两名同学玩一个游戏:在一个不透明的口袋中装有标号分别为1,2,3,4的四个小球(除标号外无其它差异),从口袋中随机摸出一个小球,记下标号后放回口袋中,充分摇匀后,再从口袋中随机摸出一个小球,记下该小球的标号,两次记下的标号分别用x、y表示.若x+y为奇数,则甲获胜;若x+y为偶数,则乙获胜. (1)用列表法或树状图法(树状图也称树形图)中的一种方法,求(x,y)所有可能出现的结果总数; (2)你认为这个游戏对双方公平吗?请说明理由. 20. (本小题8分)如图,四边形ABCD中,对角线AC、BD相交于点O,AO=OC,BO=OD,且∠AOB=2∠OAD. (1)求证:四边形ABCD是矩形; (2)若∠AOB∶∠ODC=4∶3,求∠ADO的度数. 第20题图 21. (本小题8分)已知k是常数,抛物线y=x2+(k2+k-6)x+3k的对称轴是y轴,并且与x轴有两个交点. (1)求k的值; (2)若点P在抛物线y=x2+(k2+k-6)x+3k上,且P到y轴的距离是2,求点P的坐标. 22. (本小题9分)某驻村扶贫小组实施产业扶贫,帮助贫困农户进行西瓜种植和销售.已知西瓜的成本为6元/千克,规定销售单价不低于成本,又不高于成本的两倍.经过市场调查发现,某天西瓜的销售量y(千克)与销售单价x(元/千克)的函数关系如下图所示: (1)求y与x的函数解析式(也称关系式); (2)求这一天销售西瓜获得的利润W的最大值. 23. (本小题12分)如图,AB是⊙C的直径,M、D两点在AB的延长线上,E是⊙C上的点,且DE2=DB·DA,延长AE至F,使AE=EF,设BF=10,cos∠BED=. (1)求证:△DEB∽△DAE; (2)求DA,DE的长; (3)若点F在B、E、M三点确定的圆上,求MD的长. 第23题图 一、填空题(每小题3分,共18分) 1. -6 【解析】根据具有相反意义的量的概念,零下6 ℃记作-6 ℃. 2. (x-1)2 【解析】根据完全平方公式a2-2ab+b2=(a-b)2,可得x2-2x+1=x2-2·x·1+12=(x-1)2. 3. 140 【解析】如解图,∵∠1=40°,∴∠3=∠1=40°.∵AB∥CD,∴∠2+∠3=180°.∴∠2=180°-∠3=180°-40°=140°. 第3题解图 4. 15 【解析】把(3,5)代入y= 中,得5=,解得k=15. 5. 甲班 【解析】根据甲班数学成绩频数分布直方图可知,甲班D等级人数为13人;根据乙班数学成绩扇形统计图可得,乙班D等级人数为:40×30%=12人 ,∴D等级这一组人数较多的班是甲班. 6. 16或8 【解析】情况有两种:(1)如解图①,当∠ABD是锐角时, 过点D作DE⊥AB于点E,则∠AED=∠DEB=90°,在Rt△AED中,∵∠A=30°,AD=4 ,∴DE=AD=2,AE=AD·cos30°=6, 在Rt△DEB中,∵DB=4,DE=2,∴EB==2 .∴AB=6+2=8, ∴S▱ABCD=8×2=16 .(2)如解图②, 当∠ABD是钝角时,过点D作DE⊥AB交AB延长线于点E,则∠AED =90°,在Rt△AED中,∵∠A=30°,AD=4 ,∴DE=AD=2,AE=AD·cos30°=6, 在Rt△DEB中,∵DB=4,DE=2,∴EB==2, ∴AB=6-2=4, ∴S▱ABCD=4×2=8 .综上所述,平行四边形ABCD的面积为16或8. 第6题解图 二、选择题(每小题4分,共32分) 7. B 【解析】A,C,D选项的图形是轴对称图形,不是中心对称图形;B 选项的图形既是轴对称图形,又是中心对称图形. 8. C 【解析】将一个大于10的数用科学记数法表示,其形式为a×10n ,其中1≤|a|<10 ,n为原数的整数位数减1,故688000=6.88×105 . 9. D 【解析】根据n边形内角和公式(n-2)×180°,可得十二边形的内角和为(12-2)×180°=1800°. 10. B 【解析】要使有意义,则x+1≥0,解得x≥-1. 11. A 【解析】如解图,圆锥侧面展开图的半圆弧的长为8π ,∴2π·OB=8π,∴OB=4, ∴S全=S圆锥底面+S圆锥侧面=π·42+×π·82=48π . 第11题解图 12. C 【解析】单项式的系数符号规律为:处在奇数位置上的单项式的系数符号为正,处在偶数位置上的单项式的系数符号为负,故第n个数的符号为(-1)n-1;x的指数规律为:3=2×1+1,5=2×2+1,7=2×3+1,…, ∴第n个单项式的x的指数为2n+1, ∴第n个单项式为(-1)n-1x2n+1. 13. A 【解析】如解图,连接AO,BO,CO,DO,∵△ABC的内切圆⊙O与BC,CA,AB分别相切于点D,E,F,∴OD⊥BC,OE⊥CA,OF⊥AB.∴∠OEA=∠OFA=90°.∵AB2+CA2=52+122=169,BC2=132=169,∴AB2+CA2= BC2.∴∠BAC=90°.∴∠OEA=∠OFA=∠BAC =90°.∴四边形AEOF是矩形.∵OD=OE=OF,∴四边形AEOF是正方形.设⊙O的半径为r,∵S△BOC+S△AOC+S△AOB=S△ABC,∴BC·OD+CA·OE+AB·OF=AB·AC,即(BC+CA+AB)·r=AB·AC,∴(13+12+5)·r=×5×12, 解得r=2. ∴S正方形AEOF=22=4 . 第13题解图 14. D 【解析】解不等式2(x-1)>2,得x>2, 解不等式a-x<0得,x>a, ∵不等式组的解集是x>a, ∴a≥2. 三、解答题 15. 解:原式=9+1-2-1(4分) =7.(6分) 16. 证明:在△ABC和△ADC中, (3分) ∴△ABC≌△ADC(SSS).(4分) ∴∠B=∠D.(6分) 17. 解:(1)这15名销售人员该月销售量数据的平均数为278,中位数为180,众数为90;(4分) (2)中位数最适合作为月销售目标.理由如下: 在这15人中,月销售额不低于278(平均数)件的有2人,月销售额不低于180(中位数)件的有8人,月销售额不低于90(众数)件的有15人. 所以,如果想让一半左右的营业员都能够达到月销售目标,(1)中的平均数、中位数、众数中,中位数最适合作为月销售目标.(8分) 18. 解:设甲校师生所乘大巴车的平均速度为x km/h,则乙校师生所乘大巴车的平均速度为1.5 x km/h. 根据题意得-=1.(3分) 解得x=60, 经检验,x=60是原分式方程的解,且符合题意. ∴x=60,1.5x=90. 答:甲、乙两校师生所乘大巴车的平均速度为60 km/h和90 km/h.(6分) 19. 解:(1)方法一:列表如下: x y 1 2 3 4 1 (1,1) (1,2) (1,3) (1,4) 2 (2,1) (2,2) (2,3) (2,4) 3 (3,1) (3,2) (3,3) (3,4) 4 (4,1) (4,2) (4,3) (4,4) 由列表可知,(x,y)所有可能出现的结果共有16种;(4分) 方法二:画树状图如解图: 第19题解图 由树状图可知,(x,y)所有可能出现的结果共有16种.(4分) (2)这个游戏对双方公平.理由如下: 由列表法或树状图法可知,在16种可能出现的结果中,它们出现的可能性相等. ∵x+y为奇数的有8种情况, ∴P(甲获胜)==. ∵x+y为偶数的有8种情况, ∴P(乙获胜)==. ∴P(甲获胜)=P(乙获胜). ∴这个游戏对双方公平.(7分) 20. (1)【思维教练】 要证四边形ABCD是矩形,可证,由已知条件可推出四边形ABCD是平行四边形, 继而可推出AO=AC,OD=BD ;由可推出∠OAD=∠ODA,继而可推出AO=OD,AC=BD. 证明:∵AO=OC,BO=OD, ∴四边形ABCD是平行四边形.(1分) 又∵∠AOB=2∠OAD,∠AOB是△AOD的外角, ∴∠AOB=∠OAD+∠ADO. ∴∠OAD=∠ADO.(2分) ∴AO=OD.(3分) 又∵AC=AO+OC=2AO,BD=BO+OD=2OD, ∴AC=BD. ∴四边形ABCD是矩形;(4分) (2)【思维教练】 可根据∠DOC+∠OCD+∠CDO=180°列方程求出∠ADO的度数. 解:设∠AOB=4x,∠ODC=3x,则∠ODC=∠OCD=3x.(5分) 在△ODC中,∠DOC+∠OCD+∠CDO=180°.(6分) ∴4x+3x+3x=180°,解得x=18°.(7分) ∴∠ODC=3×18°=54°. ∴∠ADO=90°-∠ODC=90°-54°=36°.(8分) 21. (1)【思维教练】 已知抛物线y=x2+(k2+k-6)x+3k的对称轴是y轴,可根据对称轴为直线x=-,列出方程k2+k-6=0,从而求出k值,得出抛物线的解析式.再根据抛物线与x轴有两个交点的条件,判断求出的k值是否符合题意. 解:∵抛物线y=x2+(k2+k-6)x+3k的对称轴是y轴, ∴x=-=0,即k2+k-6=0. 解得k=-3或k=2.(2分) 当k=2时,抛物线解析式为y=x2+6,它的图象与x轴无交点,不符合题意,舍去. 当k=-3时,抛物线解析式为y=x2-9,它的图象与x轴有两个交点,符合题意. ∴k=-3;(4分) (2)【思维教练】 根据点P到y轴距离是2,确定点P的横坐标为±2,把x=±2分别代入抛物线解析式,求出对应的纵坐标的值. 解:∵点P到y轴的距离为2, ∴点P的横坐标为-2或2. 当x=2时,y=-5; 当x=-2时,y=-5.(6分) ∴点P的坐标为(2,-5)或(-2,-5).(8分) 22. (1)【思维教练】 可根据自变量x的取值范围①6≤x≤10和②10查看更多
相关文章
- 当前文档收益归属上传用户
- 下载本文档