- 2021-04-14 发布 |
- 37.5 KB |
- 3页

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
第1章勾股定理复习学案
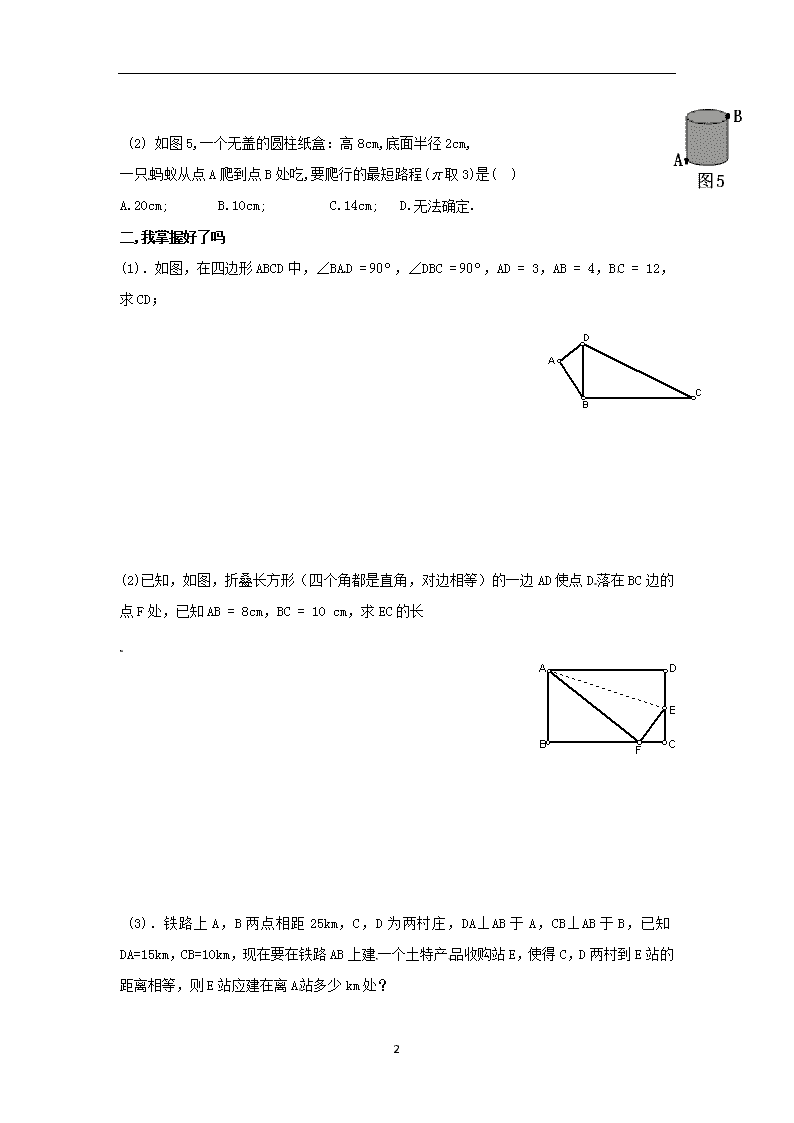
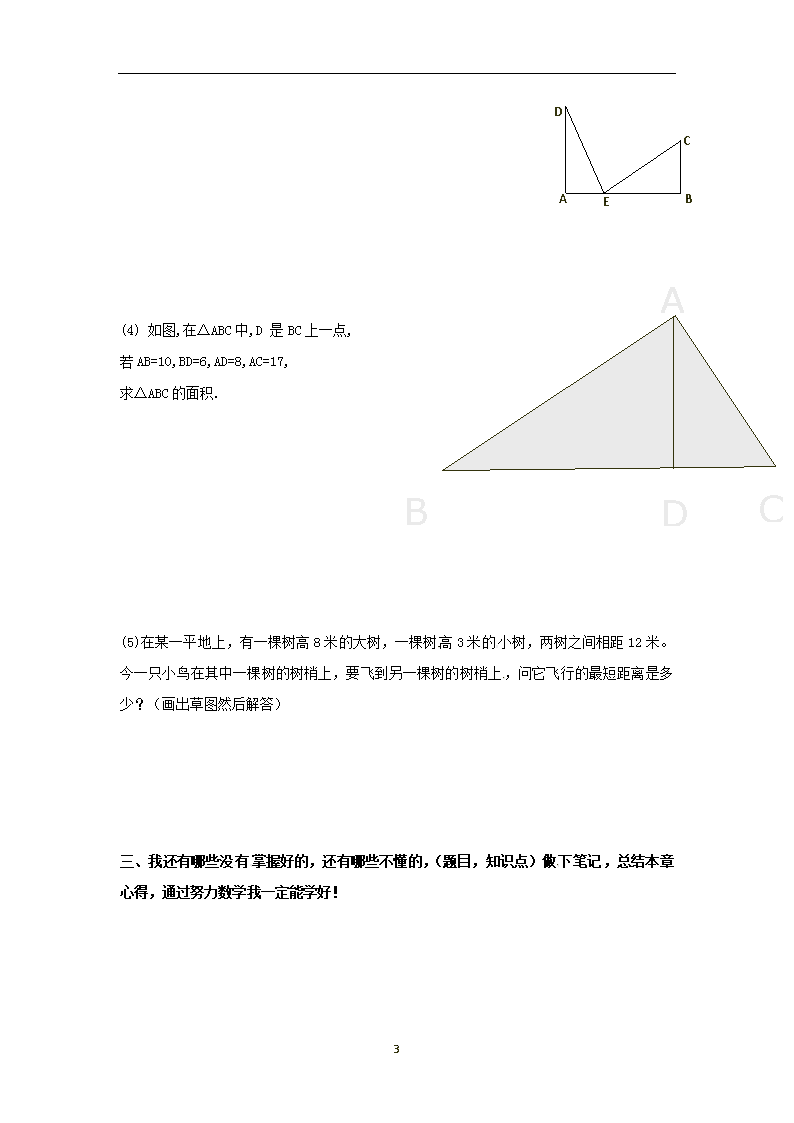
第一章 《勾股定理》复习学案 我应该非常熟练的知识点 一、勾股定理:___________________________________ 在Rt△ABC中,∠C=90°则有________________ 知识运用 (1)在Rt△ABC中,∠C=90°(1)若a=3,b=4,则c=____; 若b=8,c=17,则a=_______; (2)等腰△ABC中,AB=AC=17cm,BC=16cm,则BC边上的高AD=_______。。 图2 (3)如图2:在一个高6米,长10米的楼梯表面铺地毯, 则该地毯的长度至少是 米。 (4)一根旗杆在离地面9 m处断裂,旗杆顶部落在离旗杆底部12 m的地面上,旗杆在折断之前高度为 。 (5).一直角三角形两条边长分别是12和5,则第三边平方为 二、勾股定理逆定理_____________________________________ 知识运用 (1)、下列各组数中不能作为直角三角形的三边长的是( ) A. 1.5,2,3; B. 7,24,25; C. 6,8,10; D. 9,12,15. (2)、将直角三角形的三条边长同时扩大同一倍数, 得到的三角形是( ) A. 钝角三角形; B. 锐角三角形; C. 直角三角形; D. 等腰三角形. (3)在△ABC中,若其三条边的长度分别为9、12、15,则以两个这样的三角形所拼成的长方形的面积是____。 B A 三、最短距离问题:主要运用的依据是______________________________ (1)、如图1:有一长70㎝,宽50㎝,高50㎝的长方体盒子, A点处有一只蚂蚁,想吃到B点处的食物,它爬行的 最近距离是 厘米。 3 (2) 如图5,一个无盖的圆柱纸盒:高8cm,底面半径2cm, 一只蚂蚁从点A爬到点B处吃,要爬行的最短路程(取3)是( ) A.20cm; B.10cm; C.14cm; D.无法确定. 二,我掌握好了吗 (1).如图,在四边形ABCD中,∠BAD =,∠DBC =,AD = 3,AB = 4,BC = 12,求CD; (2)已知,如图,折叠长方形(四个角都是直角,对边相等)的一边AD使点D落在BC边的点F处,已知AB = 8cm,BC = 10 cm,求EC的长 (3).铁路上A,B两点相距25km,C,D为两村庄,DA⊥AB于A,CB⊥AB于B,已知DA=15km,CB=10km,现在要在铁路AB上建一个土特产品收购站E,使得C,D两村到E站的距离相等,则E站应建在离A站多少km处? 3 A D E B C A B C D (4) 如图,在△ABC中,D 是BC上一点, 若AB=10,BD=6,AD=8,AC=17, 求△ABC的面积. (5)在某一平地上,有一棵树高8米的大树,一棵树高3米的小树,两树之间相距12米。今一只小鸟在其中一棵树的树梢上,要飞到另一棵树的树梢上,问它飞行的最短距离是多少?(画出草图然后解答) 三、我还有哪些没有掌握好的,还有哪些不懂的,(题目,知识点)做下笔记,总结本章心得,通过努力数学我一定能学好! 3查看更多