【数学】2020届天津一轮复习通用版7-1不等式及其解法作业

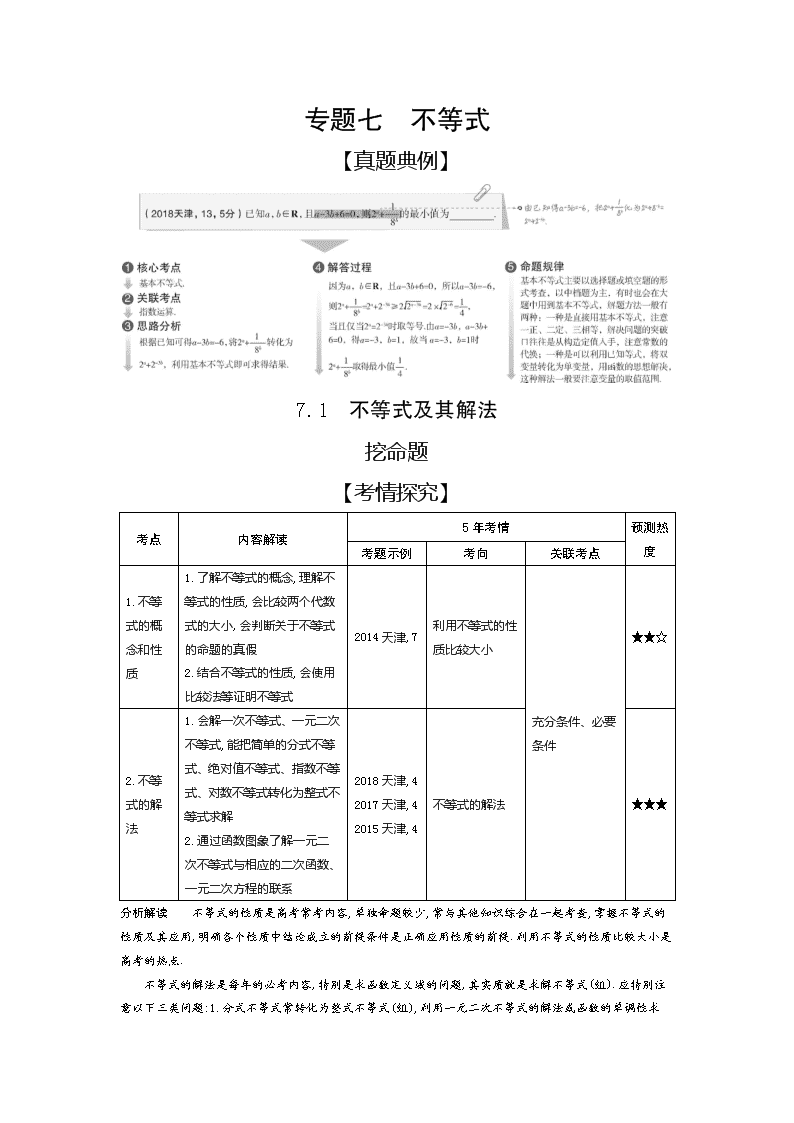
【数学】2020届天津一轮复习通用版7-1不等式及其解法作业

专题七　不等式 ‎【真题典例】‎ ‎7.1　不等式及其解法 挖命题 ‎【考情探究】‎ 考点 内容解读 ‎5年考情 预测热度 考题示例 考向 关联考点 ‎1.不等式的概念和性质 ‎1.了解不等式的概念,理解不等式的性质,会比较两个代数式的大小,会判断关于不等式的命题的真假 ‎2.结合不等式的性质,会使用比较法等证明不等式 ‎2014天津,7‎ 利用不等式的性质比较大小 充分条件、必要条件 ‎★★☆‎ ‎2.不等式的解法 ‎1.会解一次不等式、一元二次不等式,能把简单的分式不等式、绝对值不等式、指数不等式、对数不等式转化为整式不等式求解 ‎2.通过函数图象了解一元二次不等式与相应的二次函数、一元二次方程的联系 ‎2018天津,4‎ ‎2017天津,4‎ ‎2015天津,4‎ 不等式的解法 ‎★★★‎ 分析解读　　不等式的性质是高考常考内容,单独命题较少,常与其他知识综合在一起考查,掌握不等式的性质及其应用,明确各个性质中结论成立的前提条件是正确应用性质的前提.利用不等式的性质比较大小是高考的热点.‎ 不等式的解法是每年的必考内容,特别是求函数定义域的问题,其实质就是求解不等式(组).应特别注意以下三类问题:1.分式不等式常转化为整式不等式(组),‎ 利用一元二次不等式的解法或函数的单调性求解;2.以不等式恒成立为背景求参数的取值范围,一般是将参数分离出来转化为函数的最值问题来求解;3.与三角函数、解析几何、数列等知识结合起来,可以类比函数的单调性或转化为函数的单调性问题来求解.‎ 本节内容在高考中分值为5分左右,属中档偏易题.‎ 破考点 ‎【考点集训】‎ 考点一　不等式的概念和性质 ‎1.已知非零实数a,b满足a0　　　　B.‎1‎a>‎1‎b　　　　C.abb,则(　　)‎ A.ac>bc　　　　B.‎1‎a<‎1‎b　　　　C.a2>b2　　　　D.a3>b3‎ 答案　D　‎ 考点二　不等式的解法 ‎3.若集合A={x|-30},则A∩B=(　　)‎ A.{x|-3-3}‎ 答案　B　‎ ‎4.已知集合A={x|2x-1>1},B={x|x(x-2)<0},则A∩B=　　　　　　　　. ‎ 答案　{x|1b2　　　　B.1>‎1‎‎2‎b>‎1‎‎2‎a　　　　C.ba+ab<2　　　　D.aeb>bea 答案　D　‎ ‎2.已知a,b∈R,且a>b,则下列不等式一定成立的是(　　)‎ A.a2-b2>0　　　　B.cos a-cos b>0　　　　C.‎1‎a-‎1‎b<0　　　　D.e-a-e-b<0‎ 答案　D　‎ 方法2　比较实数大小的常用方法 ‎3.(2017山东,7,5分)若a>b>0,且ab=1,则下列不等式成立的是(　　)‎ A.a+‎1‎by>0,则(　　)‎ A.‎1‎x>‎1‎y　　　　B.‎1‎‎2‎x>‎1‎‎2‎y　　　　C.cos x>cos y　　　　D.ln(x+1)>ln(y+1)‎ 答案　D　‎ 方法3　一元二次不等式恒成立问题的解法 ‎5.不等式ax2-x+a>0对任意x∈(1,+∞)恒成立,则实数a的取值范围是　　　　. ‎ 答案　‎‎1‎‎2‎‎,+∞‎ ‎6.已知不等式mx2-2x-m+1<0.‎ ‎(1)是否存在实数m对所有的实数x,不等式恒成立?若存在,求出m的取值范围;若不存在,请说明理由;‎ ‎(2)设不等式对于满足|m|≤2的一切m的值都成立,求x的取值范围.‎ 解析　(1)不存在.理由如下:‎ 不等式mx2-2x-m+1<0恒成立,‎ 即函数f(x)=mx2-2x-m+1的图象全部在x轴下方.‎ 当m=0时,原不等式可化为1-2x<0,则x>‎1‎‎2‎,不满足题意;‎ 当m≠0时,函数f(x)=mx2-2x-m+1为二次函数,‎ 需满足其图象开口向下且与x轴无交点,‎ 即m<0,‎Δ=4-4m(1-m)<0,‎易知无解.‎ 综上可知,不存在满足题意的实数m.‎ ‎(2)从形式上看,原不等式是一个关于x的一元二次不等式,可以换个角度,把它看成关于m的一元一次不等式,并且已知它的解集为[-2,2],求参数x的范围.‎ 设g(m)=(x2-1)m+(1-2x),‎ 要满足题意,只需g(-2)<0,‎g(2)<0,‎ 即‎-2x‎2‎-2x+3<0,‎‎①‎‎2x‎2‎-2x-1<0,‎‎②‎ 解①得x<‎-1-‎‎7‎‎2‎或x>‎-1+‎‎7‎‎2‎,解②得‎1-‎‎3‎‎2‎b”是“a|a|>b|b|”的(　　)‎ A.充分不必要条件　　　　B.必要不充分条件　　　　C.充要条件　　　　D.既不充分又不必要条件 答案　C　‎ 考点二　不等式的解法 ‎　(2015天津,4,5分)设x∈R,则“|x-2|<1”是“x2+x-2>0”的(　　)‎ A.充分而不必要条件 B.必要而不充分条件　　　　‎ C.充要条件 D.既不充分也不必要条件 答案　A　‎ B组　统一命题、省(区、市)卷题组 考点一　不等式的概念和性质 ‎1.(2018课标Ⅲ,12,5分)设a=log0.20.3,b=log20.3,则(　　)‎ A.a+bb>0,cbd　　　　B.acbc　　　　D.ad<‎bc 答案　D　‎ ‎3.(2014山东,5,5分)已知实数x,y满足ax‎1‎y‎2‎‎+1‎　　　　B.ln(x2+1)>ln(y2+1)　　　　C.sin x>sin y　　　　D.x3>y3‎ 答案　D　‎ 考点二　不等式的解法 ‎1.(2015山东,5,5分)不等式|x-1|-|x-5|<2的解集是(　　)‎ A.(-∞,4)　　　　B.(-∞,1)　　　　C.(1,4)　　　　D.(1,5)‎ 答案　A　‎ ‎2.(2015广东文,11,5分)不等式-x2-3x+4>0的解集为　　　　.(用区间表示) ‎ 答案　(-4,1)‎ C组　教师专用题组 考点一　不等式的概念和性质 ‎1.(2016浙江,8,5分)已知实数a,b,c.(　　)‎ A.若|a2+b+c|+|a+b2+c|≤1,则a2+b2+c2<100‎ B.若|a2+b+c|+|a2+b-c|≤1,则a2+b2+c2<100　　　　C.若|a+b+c2|+|a+b-c2|≤1,则a2+b2+c2<100‎ D.若|a2+b+c|+|a+b2-c|≤1,则a2+b2+c2<100‎ 答案　D　‎ ‎2.(2014课标Ⅰ,9,5分)不等式组x+y≥1,‎x-2y≤4‎的解集记为D.有下面四个命题:‎ p1:∀(x,y)∈D,x+2y≥-2,‎ p2:∃(x,y)∈D,x+2y≥2,‎ p3:∀(x,y)∈D,x+2y≤3,‎ p4:∃(x,y)∈D,x+2y≤-1.‎ 其中的真命题是(　　)‎ A.p2,p3　　　　B.p1,p2　　　　C.p1,p4　　　　D.p1,p3‎ 答案　B　‎ ‎3.(2013陕西,10,5分)设[x]表示不大于x的最大整数,则对任意实数x,y,有(　　)‎ A.[-x]=-[x]　　　　B.[2x]=2[x]　　　　C.[x+y]≤[x]+[y]　　　　D.[x-y]≤[x]-[y]‎ 答案　D　‎ 考点二　不等式的解法 ‎1.(2013广东,9,5分)不等式x2+x-2<0的解集为　　　　. ‎ 答案　{x|-20时, f(x)=x2-4x,则不等式f(x)>x的解集用区间表示为　　　　　　　　. ‎ 答案　(-5,0)∪(5,+∞)‎ ‎3.(2013四川,14,5分)已知f(x)是定义域为R的偶函数,当x≥0时, f(x)=x2-4x.那么,不等式f(x+2)<5的解集是　　　　. ‎ 答案　(-7,3)‎ ‎【三年模拟】‎ 一、选择题(每小题5分,共50分)‎ ‎1.(2018天津和平一模,5)设x∈R,则“|x+2|+|x-1|≤5”是“-2≤x≤3”的(　　)‎ A.充分不必要条件　　　　B.必要不充分条件　　　　C.充要条件　　　　D.既不充分也不必要条件 答案　D　‎ ‎2.(2018天津河东二模,4)设x∈R,则“|x|-1>2x”是“‎1‎x+1‎≤0”的(　　)‎ A.必要不充分条件　　　　B.充分不必要条件　　　　C.充要条件　　　　D.既不充分也不必要条件 答案　A　‎ ‎3.(2019届天津新华中学期中,4)对于实数a>0,“‎1‎x‎1‎a”的(　　)‎ A.充分不必要条件　　　　B.必要不充分条件　　　　C.充要条件　　　　D.既不充分也不必要条件 答案　B　‎ ‎4.(2018天津实验中学热身训练,4)命题p:|x+2|>2,命题q:‎1‎‎3-x>1,则¬q是¬p成立的(　　)‎ A.充分不必要条件　　　　B.必要不充分条件　　　　C.充要条件　　　　D.既不充分也不必要条件 答案　B　‎ ‎5.(2018天津一中3月月考,1)已知集合A=x|‎1‎‎2‎<‎2‎x≤2‎,B=x|lnx-‎‎1‎‎2‎≤0‎,则A∩(∁RB)=(　　)‎ A.⌀　　　　B.‎-1,‎‎1‎‎2‎　　　　C.‎1‎‎2‎‎,1‎　　　　D.(-1,1]‎ 答案　B　‎ ‎6.(2018天津南开三模,3)命题“∀x∈[1,2],x2-a≤0”为真命题的一个充分不必要条件是(　　)‎ A.a≥4　　　　B.a≤4　　　　C.a≥5　　　　D.a≤5‎ 答案　C　‎ ‎7.(2017天津河北二模,5)已知条件p:|x+1|>2,条件q:x>a,且¬p是¬q的充分不必要条件,则a的取值范围是(　　)‎ A.a≤1　　　　B.a≤-3　　　　C.a≥-1　　　　D.a≥1‎ 答案　D　‎ ‎8.(2017天津和平三模,5)若不等式|x-1|+|x+m|≤4的解集非空,则实数m的取值范围是(　　)‎ A.[-5,-3]　　　　B.[-3,5]　　　　C.[-5,3]　　　　D.[3,5]‎ 答案　C　‎ ‎9.(2017天津河西三模,6)若存在实数x,使|x-a|+|x-1|≤3成立,则实数a的取值范围是(　　)‎ A.[-2,1]　　　　B.[-2,2]　　　　C.[-2,3]　　　　D.[-2,4]‎ 答案　D　‎ ‎10.(2017天津耀华中学二模,7)设正实数x,y满足x>‎1‎‎2‎,y>1,不等式‎4‎x‎2‎y-1‎+y‎2‎‎2x-1‎≥m恒成立,则m的最大值为(　　)‎ A.2‎2‎　　　　B.4‎2‎　　　　C.8　　　　D.16‎ 答案　C　‎ 二、填空题(每小题5分,共25分)‎ ‎11.(2019届天津耀华中学第一次月考,9)若集合A={x|2x-1|<3},B=x|‎2x+1‎‎3-x<0‎,则A∩B=　　　　. ‎ 答案　‎x|-1|x-a|对∀x∈R恒成立,则a的取值范围是　　　　. ‎ 答案　(0,1)‎ ‎14.(2018天津河东一模,13)设函数f(x)=x-‎1‎x对任意x∈[1,+∞), f(ax)+af(x)<0恒成立,则实数a的取值范围是　　　　. ‎ 答案　(-∞,-1)‎ ‎15.(2017天津一中5月月考,13)若不等式x2-2y2≤cx(y-x)对任意满足x>y>0的实数x,y恒成立,则实数c的最大值为　　　　. ‎ 答案　2‎2‎-4‎