- 2021-04-14 发布 |
- 37.5 KB |
- 10页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
黑龙江省高考适应性训练考试
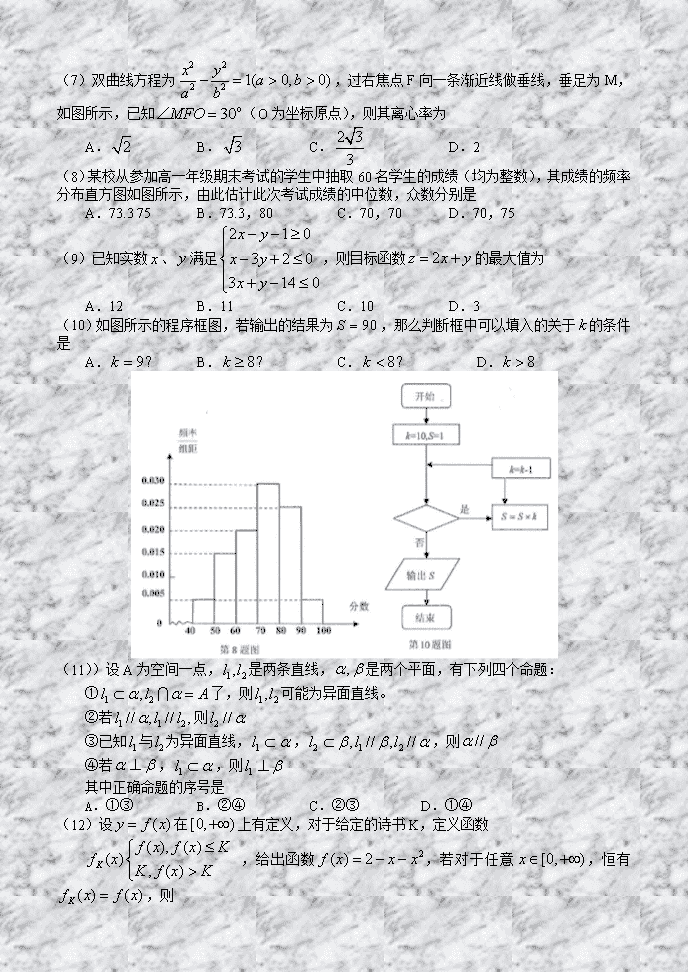
和诚教育2011届高考适应性训练考试 理科数学 本试卷分第I卷(选择题)和第II卷(非选择题)两部分。其中第II卷第(22)~(24)题为选考题,其它题为必考题。考生作答时,将答案答在答题卡上,在本试卷上答题无效。考试结束后,将本试卷和答题卡一并交回。 第I卷 一、选择题:本大题共12小题,每小题5分,在每小题给的四个选择中,只有一项是符合题目要求的。 (1)已知集合,,则= A. B. C. D. (2)复数的实部与虚部之和为 A. B.0 C.1 D.2 (3)已知平面向量,,若与垂直,则的值 A.-2 B.1 C.-1 D.2 (4)已知公差不为零的等差数列,若,且成等比数列,则其前项和为 A.90 B.100 C.110 D.120 (5)身穿红、黄两种颜色衣服的各有两人,现将这4人排成一行,要求穿相同颜色衣服的人不能相邻,则不同的排法共有( )种 A.4 B.6 C.8 D.16 (6)将的图像向左平移个单位,平移后的图像如图所示,则平移后的图像所对应的函数解析式是 A. B. C. D. (7)双曲线方程为,过右焦点F向一条渐近线做垂线,垂足为M,如图所示,已知(O为坐标原点),则其离心率为 A. B. C. D.2 (8)某校从参加高一年级期末考试的学生中抽取60名学生的成绩(均为整数),其成绩的频率分布直方图如图所示,由此估计此次考试成绩的中位数,众数分别是 A.73.3 75 B.73.3,80 C.70,70 D.70,75 (9)已知实数、满足,则目标函数的最大值为 A.12 B.11 C.10 D.3 (10)如图所示的程序框图,若输出的结果为,那么判断框中可以填入的关于的条件是 A. B. C. D. (11))设A为空间一点,是两条直线,是两个平面,有下列四个命题: ①了,则可能为异面直线。 ②若则 ③已知与为异面直线,,,则 ④若,,则 其中正确命题的序号是 A.①③ B.②④ C.②③ D.①④ (12)设在上有定义,对于给定的诗书K,定义函数 ,给出函数,若对于任意,恒有,则 A.K的最大值为 B.K的最小值为 C.K的最大值为2 D.K的最小值为2 第II卷 二、填空题:本大题共4小题,每小题5分。 (13)抛物线上的点M到其焦点F的距离为4,则点M的横坐标是 。 (14)已知某空间几何体的正视图、侧视图、俯视图都是等腰直角三角形,且直角边长为1,试写满足以上条件的一个几何体的表面积 。 (15)已知,,其中满足:“,且”的概率为 。 (16)给出下列四个命题: ①如果命题“”与命题“或”都是真命题,那么命题一定是真命题 ②命题“若,则”的否命题是:“若则” ③“”是“”的充分不必要条件 ④,使得成立 其中正确命题的序号为 。 三、解答题:解答应写出文字说明,证明过程或演算步骤。 (17)(本小题满分12分) 海岛B上有一座为10米的塔,塔顶的一个观测站A,上午11时测得一游船位于岛北偏东15°方向上,且俯角为30°的C处,一分钟后测得该游船位于岛北偏西75°方向上,且俯角45°的D处。(假设游船匀速行驶) (I) 求该船行使的速度(单位:米/分钟) (II) 又经过一段时间后,油船到达海岛B的正西方向E处,问此时游船距离海岛B多远。 18.(本小题满分12分) 甲、乙两位学生参加数学竞赛培训,现分别从他们的培训期间参加的若干次预赛成中随机抽取8次,记录如下 甲:82,91,79,78,95,88,83,84 乙:92,95,80,75,83,80,90,85 (I) 画出甲、乙两位学生成绩的茎叶图; (II) 现要从中选派一人参加数学竞赛,从统计学角度,你认为派哪位学生参加合请说明理由。 (III) 若将频率视为概率,对学生甲在今后的三次数学竞赛成绩进行预测,记这三次成绩中高于80分的次数为,求的分布列及数学期望E (19)(本小题满分12分) 四棱锥中,底面是边长为2的正方形,,,且 ,点满足 (I) 求证:平面ABCD; (II) 求二面角的余弦值。 (20)(本小题满分12分) 已知,,动点P满足,记动点P的轨迹为E。 (I) 求E的方程。 (II) 曲线E的一条切线,过作发的垂线,垂足分别为M,N,求的值。 (III) 曲线E的一条切线为,与轴,分别交于A,B两点,求的最小值,并求此时切线的斜率。 (21)(本小题满分12分) 已知 (I) 求的单调区间; (II) 当时,求在定义域上的最大值; (III) 求证: 请考生在(22)(23)、(24)三题中任选一题作答,如果多做,则按所做的第一题计分,作答时用2B铅笔在答题卡上把所选题目对应题号涂黑。 (22)(本小题满分10分)选修4-1;几何证明选讲 已知中,是AC上一点,以O为圆心,OC为半径的圆交AC于D,与AB切于E,若AD=2,AE=4,求BE的长。 (23)(本小题满分10分)选修4-4,坐标系与参数方程 曲线极坐标方程为,直线参数方程为(为参数) (I) 将化为直角坐标方程。 (II) 与是否相交?若相交求出弦长,不相交说明理由。 (24)(本小题满分10分)选修4-5;不等式选讲 设函数+ (I) 求函数的值域; (II) ,求成立时的的取值范围。 和诚教育2011届高考适应性训练考试 理科数学答案 一、选择题: A D E B C 第17题图 1.C 2.B 3.C 4.A 5.C 6.B 7.D 8.A 9.B 10.D 11.A 12.D 二、填空题: (13) 3 (14) 或 (15) (16) (1)(2)(4) 三、解答题 (17)解: (Ⅰ)在RtABC中,,AB = 10,则BC = 米 ————2分 在RtABD中,,AB = 10,则BD = 10米——————4分 在RtBCD中,, 则CD = = 20米——————————————————5分 所以速度v = = 20 米/分钟—————————————————6分 (Ⅱ)在中,, 又因为,所以———————————8分 所以—————————————————————9分 在中,由正弦定理可知, 所以米——————————————12分 (18)解: (Ⅰ)茎叶图如图 甲 乙 8 4 3 2 5 1 9 8 5 0 0 3 5 0 2 5 7 8 9 ————2分 (Ⅱ)方法一: = = 85 ,但 所以选派甲合适——————————————————————6分 方法二: 假设含90分为高分,则甲的高分率为,乙的高分率为,所以派乙合适。 或:假设含85分为高分,则甲的高分率为,乙的高分率为,所以派乙合适。 (Ⅲ)甲高于80分的频率为————————————————7分 的可能取值为0、1、2、3—————————————————8分 的分布列为 0 1 2 3 P ———————————————10分 ——————————————————————12分 (19)解: (Ⅰ)正方形ABCD中,, 又,所以 所以————————————————2分 又 —————————————————4分 又 —————————————5分 (Ⅱ)方法一: 在平面PAD中,过E作//,交AD于F,过F作AC的垂线,垂足为G,连结EG, 平面ABCD, 平面ABCD, 又,平面EGF 故,所以为二面角E—AC—D的平面角———————9分 又EF = ,在ACD中,FG = EG = ——————————————————————11分 ——————————————————————12分 方法二: 建立如图所示的空间直角坐标系, 则C (2,2,0) ,E () ,= ( 2,2,0 ) , = ()——————7分 设平面ACE的法向量,则 即 取——————9分 又平面ACD的法向量为= (0,0,2) ——————————10分 ——————————————11分 由图可知,二面角的平面角为锐角, z E A G F D C B y x P 第19题图 二面角E—AC—D的余弦值为——————12分 (20)解: () 又 点轨迹是以为焦点的椭圆,, 故椭圆方程为—————————————————————3分 ()当切线斜率不存在时,切线为,此时————4分 当切线斜率存在时,设切线方程为 ,————————6分 , ,故——8分 ()由()知, ————————10分 当且仅当,即时取等号 故的最小值为3,此时斜率为—————————————12分 (21)解: (Ⅰ)定义域为,——————————————1分 ①当a = 0时,,的单调递增区间为—————2分 ②当a < 0 时,的单调递增区间为————3分 ③当a > 0时,由,则,所以的单调递增区间为, 由,则,所以的单调递减区间为——————4分 (Ⅱ)当= 1时,, 由(Ⅰ)可知在上单调递增,在上单调递减,所以 0 + 0 — 0 ——————————————————5分 由表可知的最大值为——————————————————6分 (Ⅲ)由(Ⅱ)可知(*) 两边取对数可知 即证 又由(*)式可知当时,—————9分 =———————————12分 原不等式得证 (22)解: (方法一)圆与切于,由切割线定理得 A B C E O D 第22题图 , ——————————————2分 圆的半径————————————4分 连接,则 == ∽—————————————————— 6分 = ——————————————————————8分 —————————————————— 10分 (方法二)同法1得. 都是圆O的切线 在RtABC中,+= 即 (23)解: (Ⅰ) 的直角坐标方程为————————————4分 (Ⅱ)的直角坐标方程为——————————————6分 表示以(2,0)为圆心,2为半径的圆 与相交 ——————————— 8分 相交弦长= 与相交,相交弦长为————————————————10分 (24)解: (Ⅰ) 故的值域为——————2分 (Ⅱ) ——————4分 x ① 当时, ———————————6分 ② 当时, ————————————8分 ③ 当时, 综上 ——— —————10分查看更多