- 2021-04-14 发布 |
- 37.5 KB |
- 26页


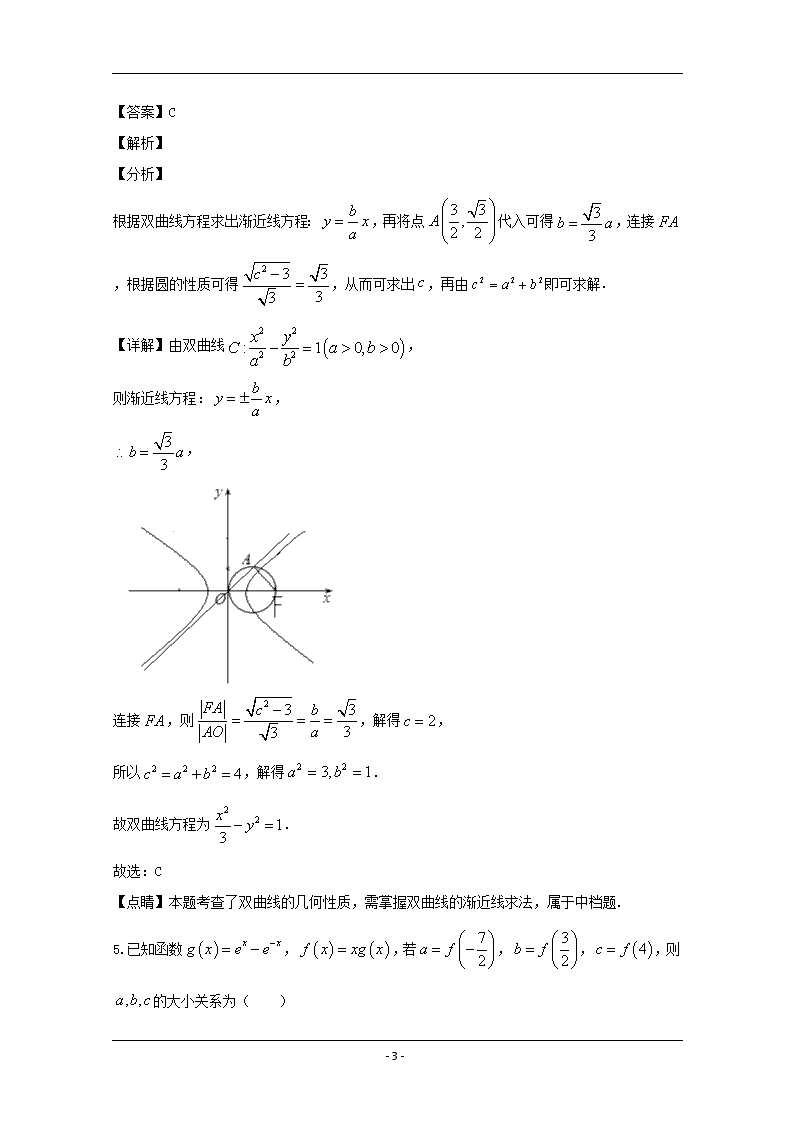
申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
山西省2020届高三模拟考试数学(理)试题 Word版含解析
- 1 - 2020 年普通高等学校招生统一模拟考试 数学理科 一、选择题 1.已知全集U R ,函数 ln 2y x 的定义域为 M ,集合 2 2 0N x x x ,则下列 结论正确的是( ) A. M N N B. UM N ð C. M N U D. UM N ð 【答案】B 【解析】 【分析】 根据函数定义域的求法,可得 M ,根据一元二次不等式的解法,可得 N ,然后根据交、并、 补计算,可得结果 【详解】令 2 0 2x x ,所以 2,M 由 2 2 0 0x x x 或 2x ,所以 ,0 2,N 0,2U N ð ,所以 UM N ð , M N M N , M N N U , UM N ð . 故选:B 【点睛】本题考查函数定义域以及一元二次不等式解法,以及交、并、补运算,重点在于掌 握交、并、补的概念以及不等式的解法,属基础题. 2.已知复数 ,z a bi a b R , 1 z i 是实数,那么复数 z 的实部与虚部满足关系式( ) A. 0a b B. 0a b C. 2 0a b D. 2 0a b 【答案】A 【解析】 【分析】 先利用复数的除法运算化简 1 z i ,若为实数,则虚部为零,即得解. 【详解】 ( )(1 ) 1 1 2 2 a b a b iz a bi a bi i i i , - 2 - 1 z i 是实数,所以 0a b , 故选:A. 【点睛】该题考查的是有关复数的问题,涉及到的知识点有复数的四则运算和基本概念,考 查了学生概念理解,数学运算的能力,属于基础题目. 3.若 1cos 4 4 ,则sin 2 的值为( ) A. 7 8 B. 7 8 C. 1 8 D. 1 8 【答案】A 【解析】 【分析】 根 据 1cos 4 4 , 将 sin 2 , 利 用 诱 导 公 式 和 二 倍 角 的 余 弦 公 式 转 化 为 2sin 2 2cos 14 求解. 【详解】因为 1cos 4 4 , 所以 2 7sin 2 cos 2 2cos 14 4 8 . 故选:A 【点睛】本题主要考查诱导公式和二倍角公式的应用,还考查了转化求解问题的能力,属于 基础题. 4.已知双曲线 2 2 2 2: 1 0, 0x yC a ba b 的右焦点为 ,F O 为坐标原点,以OF 为直径的圆 与双 曲线 C 的一条渐近线交于点O 及点 3 3,2 2A ,则双曲线C 的方程为( ) A. 2 2 13 yx B. 2 2 12 6 x y C. 2 2 13 x y D. 2 2 16 2 x y - 3 - 【答案】C 【解析】 【分析】 根据双曲线方程求出渐近线方程: by xa ,再将点 3 3,2 2A 代入可得 3 3b a ,连接 FA , 根据圆的性质可得 2 3 3 33 c ,从而可求出 c ,再由 2 2 2c a b 即可求解. 【详解】由双曲线 2 2 2 2: 1 0, 0x yC a ba b , 则渐近线方程: by xa , 3 3b a , 连接 FA ,则 2 3 3 33 FA c b AO a ,解得 2c , 所以 2 2 2 4c a b ,解得 2 23, 1a b . 故双曲线方程为 2 2 13 x y . 故选:C 【点睛】本题考查了双曲线的几何性质,需掌握双曲线的渐近线求法,属于中档题. 5.已知函数 x xg x e e , f x xg x ,若 7 2a f , 3 2b f , 4c f ,则 , ,a b c 的大小关系为( ) - 4 - A. a b c B. c b a C. b a c D. b c a 【答案】C 【解析】 【分析】 先根据函数 ( )g x 的奇偶性,判断函数 ( )f x 为偶函数,再根据偶函数的性质及单调性,即可得 答案; 【详解】依题意,有 g x g x ,则 x xg x e e 为奇函数,且在 R 上单调递增, 所以 f x 为偶函数. 当 0x 时,有 0g x g , 任取 1 2 0x x ,则 1 2 0g x g x ,由不等式的性质可得 1 1 2 2 0x g x x g x , 即 1 2 0f x f x ,所以,函数 f x 在 0, 上递增, 因此, 3 7 7 42 2 2f f f f . b a c , 故选:C. 【点睛】本题考查偶函数的性质及利用函数的单调性比较大小,考查逻辑推理能力、运算求 解能力. 6.已知某算法的程序框图如图所示,则该算法的功能是( ) - 5 - A. 求首项为1,公比为 2 的等比数列的前 2018 项的和 B. 求首项为1,公比为 2 的等比数列的前 2019 项的和 C. 求首项为1,公比为 4 的等比数列的前1009 项的和 D. 求首项为1,公比为 4 的等比数列的前1010项的和 【答案】D 【解析】 【分析】 先由程序的循环变量 n 得到循环执行的次数,再由 S 中第一次累加的是 1 12 1 ,第二次累加 的是 3 12 4 ,依此循环得到结论. 【详解】由已知中的程序框图可知:该程序的循环变量 n 的初值为1,终值为 2021,步长为 2 , 故循环共执行了1010次. 由 S 中第一次累加的是 1 12 1 ,第二次累加的是 3 12 4 ,一直下去, 故该算法的功能是求首项为1,公比为 4 的等比数列的前1010项的和. 故选:D 【点睛】本题主要考查程序框图中的循环结构,还考查了逻辑辨析的能力,属于基础题. 7.《周易》是我国古代典籍,用“卦”描述了天地世间万象变化.如图是一个八卦图,包含 乾、坤、震、巽、坎、离、艮、兑八卦(每一卦由三个爻组成,其中“ ”表示一个阳爻, “ ”表示一个阴爻).若从八卦中任取两卦,这两卦的六个爻中恰有一个阳爻的概率为 ( ) A. 3 56 B. 3 28 C. 3 14 D. 1 4 【答案】B - 6 - 【解析】 【分析】 这是一个古典概型,先算出从八卦中任取两卦的基本事件数,再根据图知仅有一个阳爻的有 坎、艮、震三卦,没有阳爻的是坤卦,得到两卦的六个爻中恰有一个阳爻的基本事件数,代 入公式求解. 【详解】从八卦中任取两卦的基本事件有 2 8 28C 卦, 由图可知,仅有一个阳爻的有坎、艮、震三卦,没有阳爻的是坤卦, 所以两卦的六个爻中恰有一个阳爻的基本事件有3 1 3 卦, 所以两卦的六个爻中恰有一个阳爻的概率 2 8 3 3 28P C . 故选:B 【点睛】本题主要考查古典概型的概率求法,还考查了理解辨析的能力,属于基础题. 8.将函数 sin 3 0f x x 的图象向右平移 8 个单位长度后,得到函数的图象关 于直线 3x 对称,则函数 f x 在 ,8 8 上的值域是( ) A. 3 ,12 B. 3,2 C. 2 ,12 D. 2,2 【答案】C 【解析】 【分析】 根据三角函数图象平移关系,结合三角函数的对称性,求出 的值,利用整体代换即可求出 函数的值域. 【详解】 sin 3f x x 0 ,向右平移 8 个单位长度后, 得到函数的解析式为 3sin 3 8f x x , 函数的图象关于直线 3x 对称, 33 3 8 2k , k Z , - 7 - 得 8k , k Z ,又 0 ,所以 7 8 π , 7sin 3 8f x x ,当 ,8 8x 时 7 53 ,8 2 4x , 7 2sin 3 ,18 2 πx . 故选:C. 【点睛】本题考查了函数图象变换规律以及正弦函数的性质,考查数形结合思想的应用,属 于中档题. 9.如图,平面四边形 ADBC 中, AB BC , 3AB , 2 3BC , ABD△ 为等边三角 形,现将 ABD△ 沿 AB 翻折,使点 D 移动至点 P ,且 PB BC ,则三棱锥 P ABC 的外接 球的表面积为( ) A. 16 B. 8 C. 4 D. 6 【答案】A 【解析】 【分析】 将三棱锥 P ABC 补形为如图所示的三棱柱,则它们的外接球相同,由此易知外接球球心O 应在棱柱上下底面三角形的外心连线上,在 Rt OBE 中,计算半径 OB 即可. 【详解】由 AB BC , PB BC ,可知 BC ⊥平面 PAB . 将三棱锥 P ABC 补形为如图所示的三棱柱,则它们的外接球相同, 由此易知外接球球心O 应在棱柱上下底面三角形的外心连线上, - 8 - 记 ABP△ 的外心为 E ,由 ABD△ 为等边三角形,可得 1BE . 又 32 BCOE ,故在 Rt OBE 中, 2OB 此即为外接球半径, 从而外接球表面积为16 . 故选:A 【点睛】本题考查了三棱锥外接球的表面积,考查了学生空间想象,逻辑推理,综合分析, 数学运算的能力,属中档题. 10.已知抛物线 2: 2 0C y px p 的焦点为 F ,准线 l ,M 是l 上一点,N 是线段 MF 与C 的交点,若 2MN NF ,O 为坐标原点,且 OFN△ 的面积 S 为 3 4 ,则 p 的值为( ) A. 2 B. 2 2 C. 3 D. 2 3 【答案】C 【解析】 【分析】 画图设点 ,N x y ,根据三角形的相似关系以及三角形面积公式可得 N 的横纵坐标关于 p 的 表达式,再联立求解即可. 【详解】假设点 M 在准线的上半部分,准线与 x 轴交点为 P ,过点 N 作 x 轴的垂线,垂足为 Q ,设点 ,N x y . 易得, ~MPF NQF△ △ ,又 2MN NF ,所以 1 1 3 3QF PF p ,则 1 6x p ①; 又 1 1 3 2 2 2 4OFN pS OF NQ y △ ,得 3y p , - 9 - 代入抛物线方程 2 2 0y px p ,得 3 3 2x p ②,联立①②得, 3p . 故选:C 【点睛】本题主要考查了根据直线与抛物线的位置关系,结合平面向量与相似比例的性质求 解参数的问题,需要根据题意设点,将横纵坐标用参数表达,进而列式求解.属于中档题. 11.设 a ,b ,c 为锐角 ABC 内角 A , B ,C 的对边,且满足 cos cos 2 3sin 3 A B C a b a , 若 2b ,则 ABC 的面积的最大值为( ) A. 3 B. 2 3 C. 2 3 3 D. 1 2 【答案】A 【解析】 【分析】 由正弦定理和题设条件,化简得3sin 2 3sin sinC B C ,进而得到 3sin 2B , 1cos 2B , 再由余弦定理和基本不等式,求得 4ac ,利用三角形的的面积公式,即可求解. 【详解】因为 cos cos 2 3sin 3 A B C a b a ,可得3 cos 3 cos 2 3 sinb A a B b C , 由正弦定理,可得 3sin cos 3sin cos 2 3sin sinB A A B B C , 又由3sin cos 3sin cos 3sin( ) 3sinB A A B A B C ,即3sin 2 3sin sinC B C , - 10 - 又由 (0, )2C ,则sin 0C ,所以 3sin 2B , 又由 (0, )2B ,所以 1cos 2B , 由余弦定理可得 2 2 2 2 22 cos 4b a c ac B a c ac , 又由 2 24 2a c ac ac ac ac ,当且 a c 时等号成立, 所以 4ac ,所以 ABC 的面积的最大值为 1 1 3sin 4 32 2 2S ac B . 故选:A. 【点睛】本题主要考查了正弦定理、余弦定理和三角形的面积公式,以及基本不等式的应用, 其中在解有关三角形的题目时,要抓住题设条件和利用某个定理的信息,合理应用正弦定理 和余弦定理求解是解答的关键,着重考查了运算与求解能力,属于基础题. 12.新型冠状病毒属于 属的冠状病毒,有包膜,颗粒常为多形性,其中包含着结构为数学模 型的 cosy B , y k b ,人体肺部结构中包含 siny A , lny ,新型冠状 病毒肺炎是由它们复合而成的,表现为 f ,若 sin 1 lnaf 在区间 0,1 上 为增函数,则 a 的取值范围为( ) A. ,0 B. ,1 C. 0, D. 1, 【答案】B 【解析】 【分析】 由题意得, 1cos 1 0f a 在 0,1 上恒成立,利用参变分离法分离出函数 ( ) cos 1g 即可求解. 【详解】∵ sin 1 lnaf 在区间 0,1 上是增函数, ∴ 1cos 1 0f a 在 0,1 上恒成立,∵ 1 0,1 0, 2 ∴ cos 1 0 ,∴ 1 cos 1a , cos 1 cos 1 sin 1 0 - 11 - cos 1 在 0,1 单调递增, cos 1 0,1 ,∴ 1 1,cos 1 ,∴ 1a . 故选:B 【点睛】本题考查已知函数单调性求参数范围问题,属于中档题. 二、填空题 13.二项式 62( )x x 的展开式中,常数项为__________. 【答案】 160 【解析】 【分析】 根据二项展开式的通项公式,即可得到答案; 【详解】 6 6 2 1 6 6 2) 2) , 0,1, ,6( (r r r rr r rT C x C x rx , 当 6 2 0 3r r 时, 4 6 33 02( 6) 1T C , 常数项为 160 , 故答案为: 160 . 【点睛】本题考查二项式定理通项公式的应用,考查运算求解能力,属于基础题. 14.已知函数 2 4 1, 0 2 2 , 0x x x xf x x ,若关于 x 的方程 1 0f x f x m 恰有 5 个不同的实根,则 m 的取值范围为______. 【答案】 (1,2) 【解析】 【分析】 转化为函数 ( )y f x 的图象与直线 1y 和直线 y m 共有 5 个不同的交点,作出函数 ( )y f x 的图象,观察图象可得结果. 【详解】由 1 0f x f x m ,得 1f x 或 f x m , 则函数 ( )y f x 的图象与直线 1y 和直线 y m 共有 5 个不同的交点, 作出函数 y f x 的图象,如图所示: - 12 - 由图可知,函数 ( )y f x 的图象与直线 1y 有两个交点, 所以函数 ( )y f x 的图象与直线 y m 有三个交点,所以 1,2m . 故答案为: (1,2) . 【点睛】本题考查了函数与方程思想,考查了数形结合思想,考查了等价转化思想,属于基 础题. 15.已知四边形 ABCD 中, AD // BC , 90BAD , 1AD , 2BC ,M 是 AB 边上的 动点,则 2MC MD 的最小值为______. 【答案】 4 【解析】 【分析】 采用建立平面直角坐标系的方法,并假设 AB m ,求得 2 MC MD 的坐标,然后根据向量 模的表示,简单计算和判断,可得结果. 【详解】建立如图的直角坐标系, 设 AB m , 0,M t , 0,t m , 由题意可知, 2,0C , 1,D m , 2,MC t , 1,MD m t , - 13 - 2 4,2 3MC MD m t , 22 16 2 3 4MC MD m t ,当且仅当 2 3 mt 时取等号, 即 2MC MD 的最小值为 4 . 故答案为:4 【点睛】本题考查利用向量的方法解决几何问题,关键在于坐标系的建立,将几何问题代数 化,向量是纽带,考验对问题的转化能力以及分析能力,属中档题. 16.波罗尼斯(古希腊数学家,约公元前 262-190 年)的著作《圆锥曲线论》是古代世界光辉 的科学成果,它将圆锥曲线的性质网罗殆尽几乎使后人没有插足的余地.他证明过这样一个命 题:平面内与两定点距离的比为常数 k( 0k 且 1k )的点的轨迹是圆,后人将这个圆称为 阿波罗尼斯圆.现有 ABC , 4,sin 2sinAC C A ,则当 ABC 的面积最大时,AC 边上的 高为_______________. 【答案】 8 3 【解析】 【分析】 ABC , 4,sin 2sinAC C A ,即 2c a .根据阿波罗尼斯圆可得:点 B 的轨迹为圆, 以 线段 AC 中点为原点,AC 所在直线为 x 轴建立直角坐标系,求出 B 的轨迹方程,进而得出结论. 【详解】解: | | sinsin 2sin , 2| | sin AB CC A CB A 为非零常数, 根据阿波罗尼斯圆可得:点 B 的轨迹是圆. 以线段 AC 中点为原点,AC 所在直线为 x 轴建立直角坐标系 则 ( 2,0), (2,0)A C ,设 ( , )B x y ,∵ 2AB CB ∴ 2 2 2 2( 2) 2 ( 2)x y x y 2 23 3 20 12 0x y x ,整理得 2 2 210 8 3 3x y 因此,当 ABC 面积最大时,BC 边上的高为圆的半径 8 3 . - 14 - 【点睛】本题考查了阿波罗尼斯圆的应用、正弦定理、三角形面积计算公式,考查了推理能 力与计算能力,属于中档题. 三、解答题 17.在四棱锥中 P ABCD 中, PAB△ 是边长为 2 的等边三角形,底面 ABCD 为直角梯形, / /AB CD , AB BC , 1BC CD , 2PD . (1)证明: AB PD ; (2)求二面角 B PA D 的余弦值. 【答案】(1)详见解析;(2) 3 3 . 【解析】 【分析】 (1)取 AB 的中点为 M ,连接 ,DM PM ,由 PAB△ 是等边三角形可得 AB PM ,再由 底面 ABCD 为直角梯形,结合已知的边长可证得 AB DM ,于是得 AB 平面 PDM ,从 而证得结果; (2)由条件可得可知 , ,DM DC DP 两两垂直,所以以 D 为坐标原点建立直角坐标系 D xyz , 利用向量法求出二面角 B PA D 的余弦值. 【详解】(1)证明:取 AB 的中点为 M ,连接 ,DM PM ,因为 PAB△ 是等边三角形,所以 AB PM . 因为在直角梯形 ABCD 中, AB BC , 1BC CD , 2AB ,所以 2AD BD 所以 DAB 为等腰三角形,所以 AB DM 因为 PM DM M ,所以 AB 平面 PDM 因为 PD 平面 PDM ,所以 AB PD . - 15 - (2)解:因为 2PD , 1DM ,PM 为正三角形 PAB△ 的 AB 边上的高,所以 3PM . 因为 2 2 2PD DM PM ,所以 PD DM ,由(1)可知 , ,DM DC DP 两两垂直. 以 D 为坐标原点建立直角坐标系 D xyz ,则 1, 1,0A , 1,1,0B , 0,1,0C , 0,0, 2P 则 0,2,0AB , 1, 1, 2PA , 1, 1,0DA 设平面 APB 的法向量为 , ,m x y z 则 0 0 AB m PA m ,即 2 0 2 0 y x y z 令 2x 得 2,0,1m . 设平面 PAD 的法向量为 , ,n x y z 则 0 0 DA n PA n ,即 0 2 0 x y x y z 令 1x ,则 1,1,0n 2 1 3cos , 33 2 m n 因为二面角 B PA D 为锐二面角,所以其余弦值为 3 3 . 【点睛】此题考查线线垂直的证明,考查二面角的余弦值的求法,考查空间中线线、线面、 面面间的位置关系等基础知识,考查运算能力,属于中档题. 18.已知数列 1na 的前 n 项和 nS 满足 3n nS a , *n N . (1)求证数列 1na 为等比数列,并求 na 关于 n 的表达式; - 16 - (2)若 3 2 log 1n nb a ,求数列 1n na b 的前 n 项和 nT . 【答案】(1)证明详见解析; 3 12 n na ;(2) 13 36 6 22 2 n n nT n . 【解析】 【分析】 (1)因为 1 21 1 ... 1 3n n nS a a a a ,即 1 2 ... 3n na a a n a ,当 2n 时 1 2 1 1... 1 3n na a a n a ,两式相减再配凑得到数列 1na 是首项为 3 2 ,公比为 3 2 的等比数列,即可计算出数列{ 1}na 的通项公式,然后计算出数列{ }na 的通项公式; (2)根据(1)的结果计算出数列{ }nb 的通项公式,进一步计算出数列{( 1) }n na b 的通项公式, 根据通项公式的特点运用错位相减法计算出前 n 项和 nT . 【详解】(1)由题设 1 21 1 ... 1 3n n nS a a a a , 即 1 2 ... 3n na a a n a ① 当 1n 时, 1 11 3a a ,解得 1 1 2a , 当 2n 时 1 2 1 1... 1 3n na a a n a ② ①-②得 11 3 3n n na a a ,即 1 3 1 2 2n na a 1 31 1 22n na a n 又 1 31 2a 所以数列 1na 是首项为 3 2 ,公比为 3 2 的等比数列,所以 31 2 n na 故 3 12 n na . (2)由(1) 3 3 2 2 3log 1 log 2 n n nb a n ,则 31 2 n n na b n , 1 2 3 13 3 3 3 31 2 3 ...+ 12 2 2 2 2 n n nT n n - 17 - 2 3 4 13 3 3 3 3 31 2 3 ... 12 2 2 2 2 2 n n nT n n 两式相减得 1 2 3 1 11 3 3 3 3 3 3...+2 2 2 2 2 2 2 n n n nT n 13 33 1 2 2 n n n 13 36 6 22 2 n n nT n 【点睛】本题主要考查数列求通项公式,以及运用错位相减法求前 n 项和,考查学生逻辑推理 能力和数学运算能力.属中档题. 19.已知椭圆 2 2 2 2: 1 0x yC a ba b 的离心率 2 2e ,椭圆C 上的点到其左焦点 1F 的最 大距离为1 2 . (1)求椭圆的标准方程; (2)过椭圆C 左焦点 1F 的直线l 与椭圆C 交于 ,A B 两点,直线 : 2m x ,过点 1F 作直线l 的垂线与直线 m 交于点T ,求 1TF AB 的最小值和此时直线l 的方程. 【答案】(1) 2 2 12 x y ;(2)最小值为 2 2 ,此时直线l 的方程为 1x . 【解析】 【分析】 (1)根据椭圆C 上的点到其左焦点的最大距离为1 2 ,得到 1 2a c ,再由 2 2e , 联立求解即可. (2)①当直线l 的斜率不存在时,直线 l 的方程为 1x ,可分别求导 T,A,B 的坐标,然 后利用两点间距离公式求解;②当直线l 的斜率存在时,设直线 l 的方程为 1y k x ,由 - 18 - 2 2 1 12 y k x x y ,利用弦长公式求得 AB ,再由 1 1 2 y xk x ,求得交点 12,T k ,从而 得到 2 1 2 1 kTF k ,代入 1TF AB 求解. 【详解】(1)由题可知 2 2 ce a ,又椭圆C 上的点到其左焦点的最大距离为1 2 , 所以 1 2a c , 所以 2a , 1c , ∴ 2 2 1b a c , 所以椭圆C 的方程为 2 2 12 x y . (2)①当直线l 的斜率不存在时,直线 l 的方程为 1x ,则 2,0T , 所以 21, 2A , 21, 2 B ,此时 1 2 2 TF AB ; ②当直线 l 的斜率存在时,设直线l 的方程为 1y k x , 1 1,A x y , 2 2,B x y 由 2 2 1 12 y k x x y , 得 2 2 2 22 1 4 2 2 0k x k x k , 由韦达定理得 2 1 2 2 4 2 1 kx x k , 2 1 2 2 2 2 2 1 kx x k , 则 2 22 1 2 1 2 2 2 2 1 1 4 1 2 k AB k x x x x k , 联立 1 1 2 y xk x ,可得 12,T k , 所以 2 1 2 1 kTF k - 19 - 所以 2 22 2 2 1 2 2 2 2 2 2 2 11 2 1 2 22 2 1 2 2 1 2 2 1 k kTF k k k AB k k k k k k . 因为 2 21 k k 所以等号不成立. 综上, 1TF AB 的最小值为 2 2 ,此时直线l 的方程为 1x . 【点睛】本题主要考查椭圆方程的求法,直线与直线,直线与椭圆的位置关系以及最值问题, 还考查了运算求解的能力,属于中档题. 20.某工厂生产某种电子产品,每件产品合格的概率均为 p ,现工厂为提高产品声誉,要求在 交付用户前每件产品都通过合格检验,已知该工厂的检验仪器一次最多可检验 5 件该产品,且 每件产品检验合格与否相互独立.若每件产品均检验一次,所需检验费用较多,该工厂提出 以下检验方案:将产品每 k 个( 5k )一组进行分组检验,如果某一组产品检验合格,则说 明该组内产品均合格,若检验不合格,则说明该组内有不合格产品,再对该组内每一件产品 单独进行检验,如此,每一组产品只需检验一次或 1k 次.设该工厂生产1000件该产品,记 每件产品的平均检验次数为 X . (1) X 的分布列及其期望; (2)(i)试说明,当 p 越大时,该方案越合理,即所需平均检验次数越少; (ii)当 0.9p 时,求使该方案最合理时 k 的值及1000件该产品的平均检验次数. 【答案】(1)分布列详见解析,期望 11 kE X p k ;(2)(i)详见解析;(ii) 4k 时 平均检验次数最少,约 594次. 【解析】 【分析】 (1)根据每 k 个( 5k )一组进行分组检验,如果某一组产品检验合格,则说明该组内产 品均合格,若检验不合格,则说明该组内有不合格产品,再对该组内每一件产品单独进行检 验,如此,每一组产品只需检验一次或 1k 次,每件产品的平均检验次数 X 的可能取值为 1 k , 1 k k ,再利用独立事件和互斥事件求得概率列出分布列,再求期望 (2)(i)由(1)知 11 kf p p k ,根据指数函数的单调性得到 f p 在 0,1p 上单 - 20 - 调递减,从而得到结论. (ii)由(1)记 11 0.9kg k k ,则由 1g k 且取最小值时, 该方案最合理求解. 【详解】(1)由题意, X 的可能取值为 1 k ,1 k k 1 kP X pk , 1 1 kkP X pk , 故 X 的分布列为 X 1 k 1 k k P kp 1 kp 1 1 11 1k k kkE X p p pk k k (2)(i)由(1),记 11 kf p p k , 因为 0k .所以 f p 在 0,1p 上单调递减, 故 p 越大, f p 越小,即所需平均检验次数越少,该方案越合理. (ii)记 11 0.9kg k k ,当 1g k 且取最小值时,该方案最合理, 因为 1 1.1g , 2 0.69g , 3 0.604g , 4 0.594g , 5 0.61g . 所以 4k 时平均检验次数最少,约1000 0.594 594 次. 【点睛】本题主要考查离散型随机变量的的分布列,期望及其应用,还考查了运算求解的能 力,属于中档题. 21.已知函数 lnmf x n xx ( ,m n 为常数). - 21 - (1)讨论 f x 的单调性; (2)若对 0,x 有 f x n m 恒成立,且 3g x f x x n 在 1 2 1 2,x x x x x 处的导数相等,求证: 1 2 11 2ln 2g x g x . 【答案】(1)详见解析;(2)详见解析. 【解析】 【分析】 (1)利用导数,在定义域中并按 0m , 0m 讨论,可得结果. (2)根据 1f n m 并结合(1),可知 m ,然后根据 1 2 g x g x ,可得 1 2 1 1 1x x , 计算 1 2g x g x ,并使用换元法,可得 3 1 ln 4 t t t t ,结合导数,可得结果. 【详解】(1) lnmf x n xx , 2 2 1 0m m xf x xx x x 当 0m 时, 0f x 在 0x 时恒成立,则 f x 在 0, 单调递减; 当 0m 时, 若 0,x m , 0f x 若 ,x m , 0f x 所以 f x 在 0,m 单调递增,在 ,m 单调递减. (2)因为 1f n m , 而 0,x 有 1f x n m f 恒成立, 知 f x 当 1x 时有最大值 1f ,由(1)知必有 1m , 所以 1 lnf x n xx , 13 3 lng x f x x n x xx , 2 1 13g x x x ,依题意设 1 2g x g x k , - 22 - 即 2 1 1 2 2 2 1 1 3 0 1 1 3 0 kx x kx x 所以 1 2 1 1 1x x , 1 2 1 2 1 22x x x x x x 因为 1 2x x 故 1 2 4x x 所以 1 2 1 2 1 2 1 2 1 13 ln lng x g x x x x xx x 则 1 2 1 2 1 23 1 ln g x g x x x x x 令 1 2 4t x x , 3 1 lnt t t , 所以, 13 0 4t tt 所以 t 在 4, 上单调递增 4 11 2ln 2t 【点睛】本题考查函数导数的综合应用,掌握分类讨论方法以及换元法的使用,化繁为简, 考验分析问题能力,本题难点在于 m 的求取以及函数 3 1 lnt t t 的构建,属难题. 22.平面直角坐标系 xOy 中,曲线 1C 的参数方程为 1 1 cos2 2 1 sin2 x y ( 为参数),以原点为 极点,x 轴的非负半轴为极轴,建立极坐标系,曲线 2C 的极坐标方程为 2 2 2 4 cos 4sin . (1)求曲线 1C 的极坐标方程以及曲线 2C 的直角坐标方程; (2)若直线 :l y kx 与曲线 1C 、曲线 2C 在第一象限交于 ,P Q 两点,且 2OQ OP ,点 M 的坐标为 2,0 ,求 MPQ 的面积. 【答案】(1) 1 : cosC , 2 2 2 : 14 xC y ;(2) 2 3 . 【解析】 - 23 - 【分析】 (1)首先消去参数 得到 1C 直角坐标方程,再化为极坐标,根据 cos sin x y 将曲线 2C 的极 坐标化为直角坐标; (2)将 0 代入曲线 1C 、曲线 2C 的极坐标方程中,求出 P , Q ,由 2OQ OP ,可得 2 0sin , 2 0cos ,根据 MPQ OMP OMQS S S △ △ △ 可得结果. 【详解】(1)依题意消去参数 曲线 2 2 1 1 1: 2 4C x y ,即 2 2 0x y x 故 2 cos 0 ,即 cos . 因为 2 2 2 4 cos 4sin ,故 2 2 2 2cos 4 sin 4 , 即 2 24 4x y ,即 2 2 14 x y . (2)将 0 代入 2 2 2 4 cos 4sin 得 2 2 0 4 1 3sinQ 将 0 代入 cos 得 0cosP 由 2OQ OP ,得 2 P Q ,即 2 0 2 0 42cos 1 3sin , 解得 2 0 2sin 3 ,则 2 0 1cos 3 又 00 2 ,故 2 0 4 2 3 1 3sin 3Q 0 3cos 3P 故 MPQ 的面积 0 1 2sin2 3MPQ OMP OMQ Q PS S S OM △ △ △ 【点睛】本题主要考查参数方程、极坐标方程和直角坐标方程之间的转换,三角形的面积公 式的应用,属于中档题. - 24 - 23.已知函数 2 6 9 2f x x x x . (1)求不等式 1f x 的解集; (2)若正数 , ,a b c 满足 24 9 23a b c f ,求 1 4 9 a b c 的最小值. 【答案】(1) 22, 3 ;(2)196 3 . 【解析】 【分析】 (1)化简后根据绝对值中的零点将 f x 转换为分段函数,再求解即可. (2)代入可得 1 4 9 1 1 4 94 93 a b ca b c a b c ,再根据柯西不等式求最小值即可. 【详解】解:(1)化简得 3 2 1x x ①当 0x 时, 3 2 3f x x x x ,由 1f x 即 3 1x ,解得 2x ,又 0x , 所以 2 0x ; ②当 0 3x 时, 3 3f x x ,由 1f x ,即 2 3 1x ,解得 2 3x ,又 0 2x , 所以 20 3x ; ③当 3x 时, 3f x x ,不满足 1f x ,此时不等式无解; 综上,不等式 1f x 的解集为 22, 3 . (2) 24 9 2 33a b c f , 所以 1 4 9 1 1 4 94 93 a b ca b c a b c ∵ , , 0a b c ,∴由柯西不等式: 上式 2 2 2 2 2 21 1 1 12 3 2 33 a b c a b c - 25 - 2 1 1 1 12 2 3 33 a b ca b c 21 1961 4 93 3 . 当且仅当 3 14a b c 时,等号成立. 所以 1 4 9 a b c 的最小值为196 3 . 【点睛】本题主要考查了绝对值不等式的求解、柯西不等式求最小值的问题,属于中档题. - 26 -查看更多