【精品试卷】中考数学一轮复习 专题测试27： 《尺规作图》（培优提高）（教师版）（1）

【精品试卷】中考数学一轮复习 专题测试27： 《尺规作图》（培优提高）（教师版）（1）

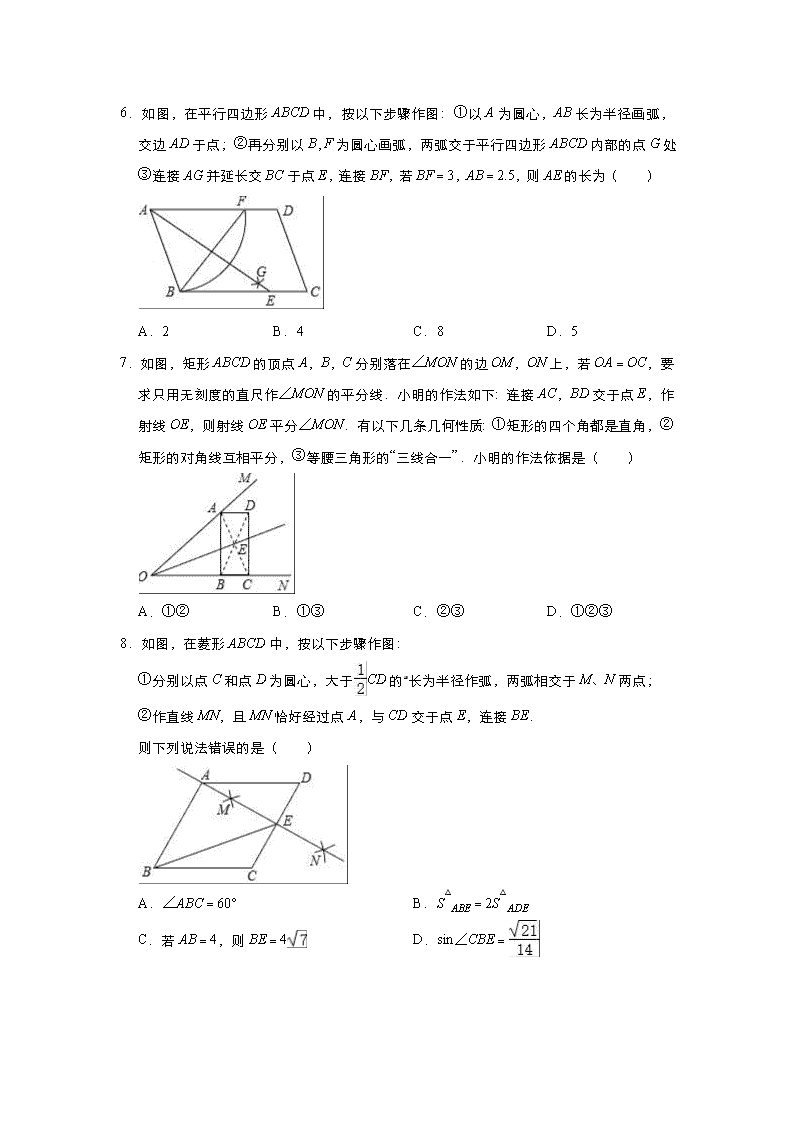
专题： 《尺规作图》（专题测试-提高） 学校:___________姓名：___________班级：___________考号：___________ 注意事项： 1．答题前填写好自己的姓名、班级、考号等信息 2．请将答案正确填写在指定位置上 第Ⅰ卷（选择题） 一．选择题（每题 4 分，共 48 分） 1．下列尺规作图分别表示：①作一个角的平分线，②作一个角等于已知角．③作一条线段 的垂直平分线．其中作法正确的是（ ） A．①② B．①③ C．②③ D．①②③ 2．如图，在 △ ABC 中，AB＝AC，以点 C 为圆心，CB 长为半径画弧，交 AB 于点 B 和点 D， 再分别以点 B，D 为圆心，大于 BD 长为半径画弧，两弧相交于点 M，作射线 CM 交 AB 于点 E．若 AE＝2，BE＝1，则 EC 的长度是（ ） A．2 B．3 C． D． 3．如图，在 △ ABC 中，∠ACB 为钝角．用直尺和圆规在边 AB 上确定一点 D．使∠ADC＝2 ∠B，则符合要求的作图痕迹是（ ） A． B． C． D． 4．根据尺规作图的痕迹，可以判定点 O 为 △ ABC 内心的是（ ） A． B． C． D． 5．已知锐角∠AOB，如图， （1）在射线 OA 上取一点 C，以点 O 为圆 心，OC 长为半径作 ，交射线 OB 于点 D， 连接 CD； （2）分别以点 C，D 为圆心，CD 长为半径作弧，交 于点 M，N； （3）连接 OM，MN． 根据以上作图过程及所作图形，下列结论中错误的是（ ） A．∠COM＝∠COD B．若 OM＝MN．则∠AOB＝20° C．MN∥CD D．MN＝3CD 6．如图，在平行四边形 ABCD 中，按以下步骤作图：①以 A 为圆心，AB 长为半径画弧， 交边 AD 于点；②再分别以 B，F 为圆心画弧，两弧交于平行四边形 ABCD 内部的点 G 处；③连接 AG 并延长交 BC 于点 E，连接 BF，若 BF＝3，AB＝2.5，则 AE 的长为（ ） A．2 B．4 C．8 D．5 7．如图，矩形 ABCD 的顶点 A，B，C 分别落在∠MON 的边 OM，ON 上，若 OA＝OC，要 求只用无刻度的直尺作∠MON 的平分线．小明的作法如下：连接 AC，BD 交于点 E，作 射线 OE，则射线 OE 平分∠MON．有以下几条几何性质：①矩形的四个角都是直角，② 矩形的对角线互相平分，③等腰三角形的“三线合一”．小明的作法依据是（ ） A．①② B．①③ C．②③ D．①②③ 8．如图，在菱形 ABCD 中，按以下步骤作图： ①分别以点 C 和点 D 为圆心，大于 CD 的 长为半径作弧，两弧相交于 M、N 两点； ②作直线 MN，且 MN 恰好经过点 A，与 CD 交于点 E，连接 BE． 则下列说法错误的是（ ） A．∠ABC＝60° B．S △ ABE＝2S △ ADE C．若 AB＝4，则 BE＝4 D．sin∠CBE＝ 9．如图，分别以线段 AB 的两个端点为圆心，大于 AB 的一半的长为半径画弧，两弧分别交 于 C，D 两点，连接 AC，BC，AD，BD，则四边形 ADBC 一定是（ ） A．正方形 B．矩形 C．梯形 D．菱形 10．已知∠AOB＝60°，以 O 为圆心，以任意长为半径作弧，交 OA，OB 于点 M，N，分别 以点 M，N 为圆心，以大于 MN 的长度为半径作弧，两弧在∠AOB 内 交于点 P，以 OP 为边作∠POC＝15°，则∠BOC 的度数为（ ） A．15° B．45° C．15° 或 30° D．15°或 45° 11．如图，直线 与 x 轴、y 轴的交点为 A，B．按以下步骤作图：①以点 A 为圆心， 适当长度为半径作弧，分别交 AB，x 轴于点 C，D；②分别以点 C，D 为圆心，大于 的长为半径作弧，两弧在∠OAB 内交于点 M；③作 射线 AM，交 y 轴于点 E．则点 E 的 坐标为（ ） A．（0， ） B．（0， ） C．（0， ） D．（0， ） 12．如图，在平面直角坐标系 xOy 中，平行四边形 OABC 的顶点 O（0，0），B（3，2），点 A 在 x 轴的正半轴上．按以下步骤作图：①以点 O 为圆心，适当长度为半径作弧分别交 边 OA、OC 于点 M、N；②分别以点 M、N 为圆心，大于 MN 的长为半径作弧 ，两弧 在∠AOC 内交于点 P；③作射线 OP，恰好过点 B，则点 A 的坐标为（ ） A．（ ，0） B．（ ，0） C．（ ，0） D．（2，0） 第Ⅱ卷（非选择题） 二．填空题（每题 4 分，共 20 分） 13．已知线段 AB 按以下步骤作图：①分别以点 A，点 B 为圆心，以 AB 长为半径作圆弧， 两弧相交于点 C；②连结 AC、BC；③以点 C 为圆心，以 CB 长为半径作圆弧，交 AC 的 延长线于点 D；④连结 BD．则∠ADB 的大小是 度． 14．如图，在 Rt △ ABC 中，∠C＝90°，∠A＝25°，按以下步骤作图：①分别以 A，B 为圆心， 以大于 的长为半径作弧，两弧交于 M，N 两点；②作直线 MN 交 AB 于点 D，交 AC 于点 E，连接 BE，则∠CBE＝ ． 15．如图，分别以 AB 的两个端点 A、B 为圆心，大于 AB 的长为半径画弧，两弧分别交于 点 P、Q，作直线 PQ 交 AB 于点 C，在 CP 上截取 CD＝AC，过点 D 作 DE∥AC，使 DE ＝AC，连接 AD、BE，当 AD＝1 时，四边形 DCBE 的面积是 ． 16．如图，在平行四边形 ABCD 中，AB＝6，BC＝10，以点 B 为圆心，以任意长为半径作 弧，分别交 BA，BC 于点 P、Q，再分别以 P、Q 为圆心，以大于 PQ 的长为半径作弧， 两弧在∠ABC 内交于点 M，连接 BM 并延长交 AD 于点 E，则 DE 的长为 ． 17．如图，Rt △ ABC 中，∠C＝90°，以点 B 为圆心，适当长为半径画弧，与∠ABC 的两边 相交于点 E，F，分别以点 E 和点 F 为圆心，大于 EF 的长为半径画弧，两弧相交于点 M，作射线 BM，交 AC 于点 D．若 AD＝10cm，∠ABC＝2∠A，则 CD 的长为 ． 三．解答题（每题 8 分，共 32 分） 18．如图，∠AOC 和∠DOB 都是直角． （1）如图 1，∠DOC＝32°，则∠AOB＝ 度； （2）在图 1 中，如果∠DOC≠32°，找出图中相等的锐角，并说明理由； （3）在图 2 中，利用三角板画一个与∠FOE 相等的角． 19．如图，已知点 A、B 以及直线 l，AE⊥l，垂足为点 E． （1）过点 B 作 BF⊥l，垂足为点 F； （2）在直线 l 上求作一点 C，使 CA＝CB； （要求：第（1）、（2）小题用尺规作图，并在图中标明相应字母，保留作图痕迹，不写 作法．） （3）在所作的图中，连接 CA、CB，若∠ACB＝90°，求证： △ AEC≌△CFB． 20．下面是“作一个 30°角”的尺规作图过程 已知射线 AB； 求作：∠PAB，使得∠PAB＝30°． 作法如图 ①在射线 AB 上取一点 O 以 O 为圆心，OA 为半径作圆，与射线 AB 相交于点 C； ②以 C 为 圆心 OC 为半径作弧，与⊙O 交于点 P，作射线 AP，所以∠PAB 即为所求的角； 根据上述的尺规作图过程 （1）使用直尺和圆规补全图形（保留作图痕迹）； （2）完成下面证明 证明：连接 PO、PC，在⊙O 和⊙C 中 ∵OP＝OC＝ ． ∴△POC 是等边三角形（ ）（填推理的依据） ∴∠POC＝60°（ ）填推理的依据） ∵ ＝ ∴∠PAB═ ∠PO B＝30°（ ）（填推理的依据） 21．（1）如图①，BE，DF，MN 是三根直立于地面的木杆在同一灯光下的影子，请画出第 三根木杆，（画出示意图，不用写画法） （2）如图②，小明在阳光下利用标杆 AB 测量校园内一棵小树 CD 的高度，在同一时刻 测得标杆的影长 BE 为 2m，小树的影长落在地面上的部分 DM 为 3m，落在墙上的部分 MN 为 1m，若标杆 AB 的长为 1.5m，求小树的高度 CD． 参 考答案 一．选择题 1．解：①作一个角的平分线的作法正确； ②作一个角等于已知角的方法正确； ③作一条线段的垂直平分线，缺少另一个交点，故作法错误； 故选：A． 2．解：由作法得 CE⊥AB，则∠AEC ＝90°， AC＝AB＝BE+AE＝2+1＝3， 在 Rt △ ACE 中，CE＝ ＝ ． 故选：D． 3．解：∵∠ADC＝2∠B 且∠ADC＝∠B+∠BCD， ∴∠B＝∠BCD， ∴DB＝DC， ∴点 D 是线段 BC 中垂线与 AB 的交点， 故选：B． 4．解：由基本作图得 C 选项中点 O 为∠ABC 和∠ACB 的平分线的交点，所以点 O 为 △ ABC 内心． 故选：C． 5．解：由作图知 CM＝CD＝DN， ∴∠COM＝∠COD，故 A 选项正确； ∵OM＝ON＝MN， ∴△OMN 是等边三角形， ∴∠MON＝60°， ∵CM＝CD＝DN， ∴∠MOA＝∠AOB＝∠BON＝ ∠MON＝20°，故 B 选项正确； 设∠MOA＝∠AOB＝∠BON＝α， 则∠OCD＝∠OCM＝ ， ∴∠MCD＝180°﹣α， 又∵∠CMN＝ ∠CON＝α， ∴∠MCD+∠CMN＝180°， ∴MN∥CD，故 C 选项正确； ∵MC+CD+DN＞MN，且 CM＝CD＝DN， ∴3CD＞MN，故 D 选项错误； 故选：D． 6．解：由题意得：AF＝AB，AE 为∠BAD 的角平分线， 则∠BAE＝∠FAE， 又∵四边形 ABCD 是平行四边形， 则 AD∥BC，∠BAE＝∠FAE＝∠BEA， ∴AF＝AB＝BE， 连接 EF， 则四边形 ABEF 是菱形， ∴AE 与 BF 互相垂直平分， 设 AE 与 BF 相交于点 O， OB＝ ＝1.5， 在 Rt △ AOB 中，OA＝ ＝ ＝2， 则 AE＝2OA＝4， 故选：B． 7．解：∵四边形 ABCD 为矩形， ∴AE＝CE， 而 OA＝OC， ∴OE 为∠AOC 的平分线． 故选：C． 8．解：由作法得 AE 垂直平分 CD，即 CE＝DE，AE⊥CD， ∵四边形 ABCD 为菱形， ∴AD＝CD＝2DE，AB∥DE， 在 Rt △ ADE 中，cosD＝ ＝ ， ∴∠ D＝60°， ∴∠ABC＝60°，所以 A 选项的结论正确； ∵S △ ABE＝ AB•AE，S △ ADE＝ DE•AE， 而 AB＝2DE， ∴S △ ABE＝2S △ ADE，所以 B 选项的结论正确； 若 AB＝4，则 DE＝2， ∴AE＝2 ， 在 Rt △ ABE 中，BE＝ ＝2 ，所以 C 选项的结论错误； 作 EH⊥BC 交 BC 的延长线于 H，如图， 设 AB＝4a，则 CE＝2a，BC＝4a，BE＝2 a， 在 △ CHE 中，∠ECH＝∠D＝60°， ∴CH＝a，EH＝ a， ∴sin∠CBE＝ ＝ ＝ ，所以 D 选项的结论正确． 故选：C． 9．解：由作图可知：AC＝AD＝BC＝BD， ∴四边形 ACBD 是菱形， 故选：D． 10．解：（1）以 O 为圆心，以任意长为半径作弧，交 OA，OB 于点 M，N，分别以点 M，N 为圆心， 以大于 MN 的长度为半径作弧，两弧在∠AOB 内交于点 P，则 OP 为∠AOB 的平分线， （2）两弧在∠AOB 内交于点 P，以 OP 为边作∠POC＝15°，则为作 ∠POB 或∠POA 的 角平分线， 则∠BOC＝15°或 45°， 故选：D． 11．解：过 E 作 EH⊥AB 于 H，如图， 由作法得 AE 平分∠OAB， ∴OE＝EH， 当 x＝0 时，y＝﹣ x+4＝4，则 B（0，4）， 当 y＝0 时，﹣ x+4＝0，解得 x＝3，则 A（3，0）， ∴AB＝ ＝5， 设 E（0，t）， ∵S △ AOE+S △ ABE＝S △ OAB， ∴ ×t×3+ ×t×5＝ ×3×4，解得 t＝ ， ∴E 点坐标为（0， ）． 故选：C． 12．解：由作法得 OB 平分∠AOC， ∴∠AOB＝∠COB， ∵四边形 OABC 为平行四边形， ∴AB∥OC， ∴∠COB＝∠ABO， ∴∠ABO＝∠AOB， ∴AO＝AB， 设 A（t，0）， ∴t2＝（3﹣t）2+22，解得 t＝ ， ∴A 点坐标为（ ，0 ）． 故选：A． 二．填空题（共 5 小题） 13．解：由作法得 CA＝CB＝AB，CB＝CD， ∴△ABC 为等边三角形， ∴∠ACB＝60°， 而 CB＝CD， ∴∠D＝∠CBD， 而∠ACB＝∠D+∠CBD＝60°， ∴∠D＝30°． 故答案为 30°． 14．解：∵在 Rt △ ABC 中，∠C＝90°，∠A＝25° ∴∠ABC＝90°﹣25°＝65°， 由作法得 MN 垂直平分 AB， ∴EA＝EB， ∴∠EBA＝∠A＝25°， ∴∠CBE＝∠ABC﹣∠EBA＝65°﹣25°＝40°． 故答案为 40°． 15．解：由作图可知：DC⊥AB， ∵AC＝CD，∠ACD＝90°，AD＝1， ∴AC＝DC＝BC＝ ， ∵DE＝AC＝BC，DE∥BC， ∴四边形 DCBE 是平行四边形， ∵∠DCB＝90°， ∴四边形 DCBE 是矩形， ∴四边形 DCBE 的面积＝CD•CB＝ × ＝ ， 故答案为 ． 16．解：由作图可知：∠ABE＝∠EBC， ∵四边形 ABCD 是平行四边形， ∴AD∥BC，AD＝BC＝10， ∴∠AEB＝∠EBC， ∴∠ABE＝∠AEB， ∴AB＝AE＝6， ∴DE＝AD﹣AE＝10﹣6＝4， 故答案为 4． 17．解：由题意可得：BD 是∠ABC 的角平分线， ∵∠ABC＝2∠A，在 Rt △ ABC 中，∠C＝90°， ∴∠ABC＝60°，∠A＝30°， ∴∠CBD＝∠DBA＝30°， ∴BD＝2CD， ∵∠DBA＝∠A＝30°， ∴AD＝BD， ∴AD＝2CD＝10cm， ∴CD＝5cm， 故答案为：5cm． 三．解答题（共 4 小题） 18．解：（1）∵∠AOC＝90°，即∠AOD+∠DOC＝90°， ∴∠AOD＝90°﹣32°＝58°， ∴∠AOB＝∠DOB+∠AOD＝90°+58°＝148°； 故答案为 148； （2）相等的锐角为∠AOD＝∠BOC． 理由如下： ∵∠AOD+∠DOC＝90°，∠BOC+∠DOC＝90°， ∴∠AOD＝∠BOC； （3）如图，∠MON 为所作． 19．（1）解：如图 2，直线 BF 就是要求作的垂线； （2）解：如图 2，点 C 就是所要求作的点； （3）证明∵AE⊥l， ∴∠AEC＝90°，∠1+∠2＝90°． ∵∠ACB＝90°， ∴∠3+∠2＝90°． ∴∠1＝∠3， 在 △ AEC 和 △ CFB 中 ∴△AEC≌△CFB （AAS）． 20．解：（1）如图：∠PAB 即为所求作的图形． （2）证明：连接 PO、PC，在⊙O 和⊙C 中 ∵OP＝OC＝CP． ∴△POC 是等边三角形（三条边相等的三角形是等边三角形） ∴∠POC＝60°（等边三角形的每个角都等于 60°） ∵ ＝ ∴∠PAB═ ∠POB＝30°（同弧所对的圆周角等于圆心角的一半） 故答案为：CP， 三条边相等的三角形是等边三角形， 等边三角形每个角都等于 60°， 同弧所对的圆周角等于圆心角的一半． 21．解：（1）如图①中，PM 为第三根木杆． （2）如图 2 中， 由题意可知， ． 即 ． 解得， ， 由 ，得 ． 解得 CD＝3.25． 答：小树的高度 CD 为 3.25 m．