- 2021-04-14 发布 |
- 37.5 KB |
- 10页

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
高考数学一轮复习第九章立体几何9-7-2利用空间向量求二面角与空间距离练习理北师大版
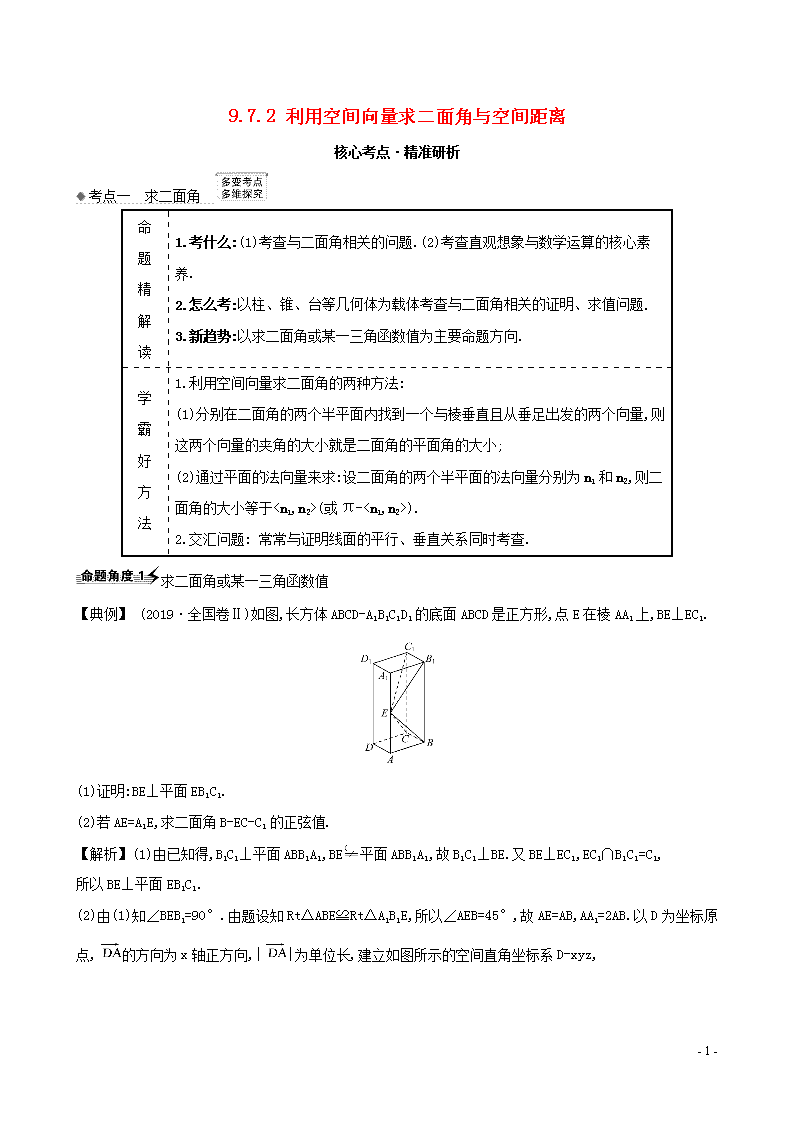
9.7.2 利用空间向量求二面角与空间距离 核心考点·精准研析 考点一 求二面角 命 题 精 解 读 1.考什么:(1)考查与二面角相关的问题.(2)考查直观想象与数学运算的核心素养. 2.怎么考:以柱、锥、台等几何体为载体考查与二面角相关的证明、求值问题. 3.新趋势:以求二面角或某一三角函数值为主要命题方向. 学 霸 好 方 法 1.利用空间向量求二面角的两种方法: (1)分别在二面角的两个半平面内找到一个与棱垂直且从垂足出发的两个向量,则这两个向量的夹角的大小就是二面角的平面角的大小; (2)通过平面的法向量来求:设二面角的两个半平面的法向量分别为n1和n2,则二面角的大小等于查看更多