高考数学理科知识点总结精辟
2018 高考数学(理科)知识点总结
1.对于集合,一定要抓住集合的代表元素,及元素的“确定性、互异性、无序性”。
中元
素各表示什么?
注重借助于数轴和文氏图解集合问题。
空集是一切集合的子集,是一切非空集合的真子集。
3. 注意下列性质:
(3)德摩根定律:
4. 你会用补集思想解决问题吗?(排除法、间接法)
的取值范围。
6. 命题的四种形式及其相互关系是什么? (互为逆否关系的命题是等价命题。)
原命题与逆否命题同真、同假;逆命题与否命题同真同假。
7. 对映射的概念了解吗?映射 f:A→B,是否注意到 A 中元素的任意性和 B 中与之对应元素的唯一性,哪几种对应能
构成映射? (一对一,多对一,允许 B 中有元素无原象。)
8. 函数的三要素是什么?如何比较两个函数是否相同? (定义域、对应法则、值域)
9. 求函数的定义域有哪些常见类型?
10.如何求复合函数的定义域? 义域是
_。
11. 求一个函数的解析式或一个函数的反函数时,注明函数的定义域了吗?
12. 反函数的性质有哪些? 互为反函数的图象关于直线 y=x 对称;
13. 如何用定义证明函数的单调性? (取值、作差、判正负) 如何判断复合函数的单调性?
∴……)
{ } { } { }如:集合 , , , 、 、A x y x B y y x C x y y x A B C= = = = = =| lg | lg ( , )| lg
2. 进行集合的交、并、补运算时,不要忘记集合本身和空集 的特殊情况。∅
{ } { }如:集合 ,A x x x B x ax= − − = = =| |2 2 3 0 1
若 ,则实数 的值构成的集合为B A a⊂ (答: , , )−
1 0 1
3
{ }( )集合 , ,……, 的所有子集的个数是 ;1 21 2a a an
n
( ) ( ) ( ) ( ) ( ) ( )C C C C C CU U U U U UA B A B A B A B = =,
( )),,
·∴,∵
·∴,∵(
2593
51
05
555
03
533
2
2
∈⇒
≥−
−∉
<−
−∈
a
a
aM
a
aM
5. 可以判断真假的语句叫做命题,逻辑连接词有“或” ,“且” 和( ) ( )∨ ∧ “非”( ).¬
若 为真,当且仅当 、 均为真p q p q∧ 至少有一个为真、为真,当且仅当若 qpqp ∨
若 为真,当且仅当 为假¬p p
[ ]如:函数 的定义域是 , , ,则函数 的定f x a b b a F(x f x f x( ) ) ( ) ( )> − > = + −0
[ ](答: , )a a−
[ ]
(内层)(外层)
,则,( )()()( xfyxuufy ϕϕ ===
u
O 1 2 x
15. 如何利用导数判断函数的单调性?
值是( ) A. 0 B. 1 C. 2 D. 3
∴a 的最大值为 3)
16. 函数 f(x)具有奇偶性的必要(非充分)条件是什么? (f(x)定义域关于原点对称)
注意如下结论: (1)在公共定义域内:两个奇函数的乘积是偶函数;两个偶函数的乘积是偶函数;一个偶函数
与奇函数的乘积是奇函数。
17. 你熟悉周期函数的定义吗?
函数,T 是一个周期。)
如:
18. 你掌握常用的图象变换了吗?
( )在区间 , 内,若总有 则 为增函数。(在个别点上导数等于a b f x f x'( ) ( )≥ 0
零,不影响函数的单调性),反之也对,若 呢?f x'( ) ≤ 0
[ )如:已知 ,函数 在 , 上是单调增函数,则 的最大a f x x ax a> = − + ∞0 13( )
由已知 在 , 上为增函数,则 ,即f x a a( ) [ )1 3 1 3+ ∞ ≤ ≤
若 总成立 为奇函数 函数图象关于原点对称f x f x f x( ) ( ) ( )− = − ⇔ ⇔
若 总成立 为偶函数 函数图象关于 轴对称f x f x f x y( ) ( ) ( )− = ⇔ ⇔
f x f x y( ) ( )与 的图象关于 轴 对称−
f x f x x( ) ( )与 的图象关于 轴 对称−
f x f x( ) ( )与 的图象关于 原点 对称− −
f x f x y x( ) ( )与 的图象关于 直线 对称− =1
f x f a x x a( ) ( )与 的图象关于 直线 对称2 − = f x f a x a( ) ( ) ( )与 的图象关于 点 , 对称− −2 0
将 图象 左移 个单位
右移 个单位
y f x a a
a a
y f x a
y f x a
= > →
>
= +
= −( ) ( )
( )
( )
( )
0
0
上移 个单位
下移 个单位
b b
b b
y f x a b
y f x a b
( )
( )
( )
( )
> →
>
= + +
= + −
0
0
注意如下“翻折”变换:
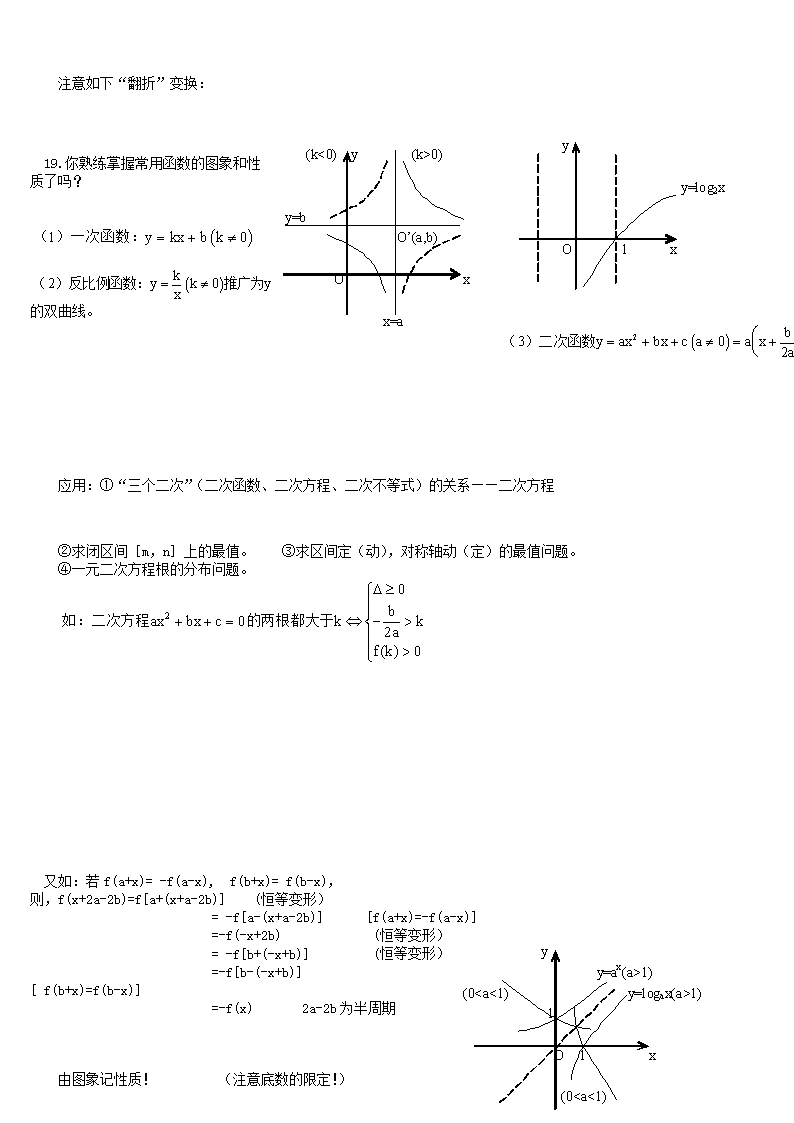
19.你熟练掌握常用函数的图象和性
质了吗?
的双曲线。
应用:①“三个二次”(二次函数、二次方程、二次不等式)的关系——二次方程
②求闭区间[m,n]上的最值。 ③求区间定(动),对称轴动(定)的最值问题。
④一元二次方程根的分布问题。
又如:若 f(a+x)= -f(a-x), f(b+x)= f(b-x),
则,f(x+2a-2b)=f[a+(x+a-2b)] (恒等变形)
= -f[a-(x+a-2b)] [f(a+x)=-f(a-x)]
=-f(-x+2b) (恒等变形)
= -f[b+(-x+b)] (恒等变形)
=-f[b-(-x+b)]
[ f(b+x)=f(b-x)]
=-f(x) 2a-2b 为半周期
由图象记性质! (注意底数的限定!)
( )( )一次函数:1 0y kx b k= + ≠
( ) ( )( )反比例函数: 推广为 是中心 ,2 0 0y k
x k y b k
x a k O a b= ≠ = + − ≠ '( )
( )( )二次函数 图象为抛物线3 0 2
4
4
2
2 2
y ax bx c a a x b
a
ac b
a
= + + ≠ = +
+ −
如:二次方程 的两根都大于ax bx c k b
a k
f k
2 0
0
2
0
+ + = ⇔
≥
− >
>
∆
( )
y
y=log2x
O 1 x
(k<0) y (k>0)
y=b
O’(a,b)
O x
x=a
y
y=ax(a>1)
(0
1)
1
O 1 x
(0
log log log log loga a a a
n
a
M
N M N M n M= − =, 1
( ) , 满足 ,证明 是偶函数。2 x R f x f xy f x f y f x∈ = +( ) ( ) ( ) ( ) ( )
又如:求函数 的定义域和值域。y x= − −
1 2 2cos
π
(∵ )1 2 2 1 2 0− −
= − ≥cos sin
π
x x
y
O x
− k
k
O R
1 弧度
R
y
T
A x
α
B S
O M
P
25. 你能迅速画出正弦、余弦、正切函数的图象吗?并由图象写出单调区间、对称点、对称轴吗?
(x,y)作图象。
27.在三角函数中求一个角时要注意两个方面——先求出某一 个 三 角
函数值,再判定角的范围。
28. 在解含有正、余弦函数的问题时,你注意(到)运用函数的有界性了吗?
∴ ,如图:sin x ≤ 2
2
( )y x k k k Z= − +
∈sin 的增区间为 ,2 2 2 2
π π π π ( )减区间为 ,2 2 2 3
2k k k Zπ π π π+ +
∈
( ) ( )图象的对称点为 , ,对称轴为k x k k Zπ π π
0 2
= + ∈ [ ] ( )y x k k k Z= + ∈cos 的增区间为 ,2 2π π π
[ ] ( )减区间为 ,2 2 2k k k Zπ π π π+ + ∈ ( )图象的对称点为 , ,对称轴为k x k k Zπ π π+
= ∈
2 0
y x k k k Z= − +
∈tan 的增区间为 ,π π π π
2 2
( ) ( )[ ]26. y = Asin x +正弦型函数 的图象和性质要熟记。 或ω ϕ ω ϕy A x= +cos
( )振幅 ,周期1 2| | | |A T = π
ω
( )若 ,则 为对称轴。f x A x x0 0= ± =
( ) ( )若 ,则 , 为对称点,反之也对。f x x0 00 0=
( )五点作图:令 依次为 , , , , ,求出 与 ,依点2 0 2
3
2 2ω ϕ π π π πx x y+
( )根据图象求解析式。(求 、 、 值)3 A ω ϕ
解条件组求 、 值ω ϕ
( )∆正切型函数 ,y A x T= + =tan | |
ω ϕ π
ω
y
x
O− π
2
π
2
π
y tgx=
29. 熟练掌握三角函数图象变换了吗? (平移变换、伸缩变换)
平移公式:
图象?
30. 熟练掌握同角三角函数关系和诱导公式了吗?
“奇”、“偶”指 k 取奇、偶数。
A. 正值或负值 B. 负值 C. 非负值 D. 正值
31. 熟练掌握两角和、差、倍、降幂公式及其逆向应用了吗?
理解公式之间的联系:
应用以上公式对三角函数式化简。(化简要求:项数最少、函数种类最少,分
母中不含三角函数,能求值,尽可能求值。)
具体方法:
(2)名的变换:化弦或化切 (3)次数的变换:升、降幂公式
( )点 ( , ) ,
平移至
( , ),则1 P x y a h k P x y x x h
y y k
→= → = +
= +
( ) ' ' ' '
'
( )曲线 , 沿向量 , 平移后的方程为 ,2 0 0f x y a h k f x h y k( ) ( ) ( )= = − − =
→
如:函数 的图象经过怎样的变换才能得到 的y x y x= −
− =2 2 4 1sin sin
π
“ · ”化为 的三角函数——“奇变,偶不变,符号看象限”,k
π α α
2
±
( )如: cos tan sin9
4
7
6 21
π π π+ −
+ = 又如:函数 ,则 的值为y y= +
+
sin tan
cos cot
α α
α α
( )( )角的变换:如 , ……1 2 2 2
β α β α α β α β α β= + − + = −
− −
(4)形的变换:统一函数形式,注意运用代数运算。
32. 正、余弦定理的各种表达形式你还记得吗?如何实现边、角转化,而解斜三角形?
(应用:已知两边一夹角求第三边;已知三边求角。)
33. 用 反 三 角 函 数 表 示 角 时 要 注 意 角 的 范 围 。
34. 不等式的性质有哪些?
答案:C
35. 利用均值不等式:
值?(一正、二定、三相等)
注意如下结论:
( ) ( )如:已知 , ,求 的值。sin cos
cos tan tan
α α
α α β β α
1 2 1 2
3 2− = − = − −
(由已知得: ,∴sin cos
sin
cos
sin tan
α α
α
α
α α
2 2 1 1
22
= = =
( ) ( )[ ] ( )
( )∴ · ·
)tan tan tan tan
tan tan
β α β α α β α α
β α α− = − − = − −
+ − =
−
+
=2 1
2
3
1
2
1 2
3
1
2
1
8
正弦定理: a
A
b
B
c
C R
a R A
b R B
c R Csin sin sin
sin
sin
sin
= = = ⇔
=
=
=
2
2
2
2
( )求角 ;1 C
( )(( )由已知式得:1 1 2 1 12− + + − =cos cosA B C
( )由正弦定理及 得:2 1
2
2 2 2a b c= +
[ ]反正弦: , , ,arcsin x x∈ −
∈ −π π
2 2 1 1
[ ] [ ]反余弦: , , ,arccosx x∈ ∈ −0 1 1π ( )反正切: , ,arctan x x R∈ −
∈π π
2 2
( )a b ab a b R a b ab ab a b2 2
2
2 2 2
+ ≥ ∈ + ≥ ≤ +
+, ; ; 求最值时,你是否注
意到“ , ”且“等号成立”时的条件,积 或和 其中之一为定a b R ab a b∈ ++ ( ) ( )
36. 不等式证明的基本方法都掌握了吗?
(比较法、分析法、综合法、数学归纳法等)
并注意简单放缩法的应用。
(移项通分,
分子分母因式分解,x 的系数变为 1,穿轴法解得结果。)
38. 用“穿轴法”解高次不等式——“奇穿,偶切”,从最大根的右上方开始
39. 解含有参数的不等式要注意对字母参数的讨论
40. 对含有两个绝对值的不等式如何去解? (找零点,分段讨论,去掉绝对值符号,最后取各段的并集。)
证明:
(按不等号方向放缩)
42. 不等式恒成立问题,常用的处理方式是什么?(可转化为最值问题,或“△”问题)
43. 等差数列的定义与性质
当且仅当 时等号成立。a b=
如:若 , 的最大值为x x x
> − −0 2 3 4
当且仅当 ,又 ,∴ 时, )3 4 0 2 3
3 2 4 3x x x x y= > = = −max
(∵ ,∴最小值为 )2 2 2 2 2 2 2 22 2 1x y x y+ ≥ =+
)…… 2121
1
1
3
1
2
1
2
111 <−=−−++−+−+=
nnn
( )37 0. ( )
( )
解分式不等式 的一般步骤是什么?f x
g x a a> ≠
例如:解不等式| |x x− − + <3 1 1 (解集为 )x x| >
1
2
41. | | | | | | | | | |会用不等式 证明较简单的不等问题a b a b a b− ≤ ± ≤ + 如:设 ,实数 满足f x x x a x a( ) | |= − + − <2 13 1
1|||||1||1|||)1||(|)1)((| ++≤−+<−+−=<−−+−= axaxaxaxaxaxax
如: 恒成立 的最小值a f x a f x< ⇔ <( ) ( ) a f x a f x> ⇔ >( ) ( )恒成立 的最大值
a f x a f x> ⇔ >( ) ( )能成立 的最小值
例如:对于一切实数 ,若 恒成立,则 的取值范围是x x x a a− + + >3 2
(设 ,它表示数轴上到两定点 和 距离之和u x x= − + + −3 2 2 3
( )定义: 为常数 ,a a d d a a n dn n n+ − = = + −1 1 1( ) 等差中项: , , 成等差数列x A y A x y⇔ = +2
( ) ( )
前 项和n S a a n na n n dn
n= + = + −1
12
1
2
{ }性质: 是等差数列a n
{ } { } { }( )数列 , , 仍为等差数列;2 2 1 2a a ka bn n n− +
0 的二次函数)
项,即:
44. 等比数列的定义与性质
46. 你熟悉求数列通项公式的常用方法吗?
例如:(1)求差(商)法
解:
[练习]
(2)叠乘法
解:
(3)等差型递推公式
( )若三个数成等差数列,可设为 , , ;3 a d a a d− +
( )若 , 是等差数列 , 为前 项和,则 ;4 2 1
2 1
a b S T n a
b
S
Tn n n n
m
m
m
m
= −
−
{ }( ) 为等差数列 ( , 为常数,是关于 的常数项为5 2a S an bn a b nn n⇔ = +
{ }S S an bn an n n的最值可求二次函数 的最值;或者求出 中的正、负分界= +2
当 , ,解不等式组 可得 达到最大值时的 值。a d a
a S nn
n
n1
1
0 0 0
0
> < ≥
≤
+
当 , ,由 可得 达到最小值时的 值。a d a
a S nn
n
n1
1
0 0 0
0
< > ≤
≥
+
{ }如:等差数列 , , , ,则a S a a a S nn n n n n= + + = = =− −18 3 11 2 3
等比中项: 、 、 成等比数列 ,或x G y G xy G xy⇒ = = ±2
( )前 项和: (要注意 )n S
na q
a q
q qn
n=
=
−
− ≠
1
1
1
1
1 1
( )
( )
! { }性质: 是等比数列a n
( ) , , ……仍为等比数列2 2 3 2S S S S Sn n n n n− −
45. 由 求 时应注意什么?S an n ( 时, , 时, )n a S n a S Sn n n= = ≥ = − −1 21 1 1
{ }如: 满足 ……a a a a nn n n
1
2
1
2
1
2 2 5 11 2 2+ + + = + < >
n a a a nn n≥ + + + = − + < >− −2 1
2
1
2
1
2 2 1 5 21 2 2 1 1时, ……
{ }数列 满足 , ,求a S S a a an n n n n+ = =+ +1 1 1
5
3 4 (注意到 代入得:a S S S
Sn n n
n
n
+ +
+= − =1 1
1 4
{ }又 ,∴ 是等比数列,S S Sn n
n
1 4 4= = n a S Sn n n
n≥ = − = =−
−2 3 41
1时, …… ·
{ }例如:数列 中, , ,求a a a
a
n
n an
n
n
n1
13 1
= = +
+
由 , ,求 ,用迭加法a a f n a a an n n− = =−1 1 0( )
[练习]
(4)等比型递推公式
[练习]
(5)倒数法
47. 你熟悉求数列前 n 项和的常用方法吗?
例如:(1)裂项法:把数列各项拆成两项或多项之和,使之出现成对互为相反数的项。
解:
[练习]
(2)错位相减法:
(3)倒序相加法:把数列的各项顺序倒写,再与原来顺序的数列相加。
n a a f
a a f
a a f nn n
≥ − =
− =
− =
−
2 2
3
2 1
3 2
1
时,
…… ……
两边相加,得:
( )
( )
( )
{ } ( )数列 , , ,求a a a a n an n
n
n n1
1
11 3 2= = + ≥−
−
( )a ca d c d c c dn n= + ≠ ≠ ≠−1 0 1 0、 为常数, , ,
( )可转化为等比数列,设a x c a xn n+ = +−1
∴ 是首项为 , 为公比的等比数列a d
c a d
c cn + −
+ −1 11
{ }数列 满足 , ,求a a a a an n n n1 19 3 4= + =+ ( )a n
n
= −
+
−
8 4
3 1
1
例如: , ,求a a a
a an
n
n
n1 11 2
2
= = ++ 由已知得: 1 2
2
1
2
1
1a
a
a an
n
n n+
= + = +
∴
=1 1 1 1
21a an
为等差数列, ,公差为
{ }如: 是公差为 的等差数列,求a d a an
k kk
n 1
11 +=
∑
求和: …… ……1 1
1 2
1
1 2 3
1
1 2 3
+ + + + + + + + + + + n
{ } { } { }若 为等差数列, 为等比数列,求数列 (差比数列)前 项a b a b nn n n n
{ }和,可由 求 ,其中 为 的公比。S qS S q bn n n n−
[练习]
48. 你知道储蓄、贷款问题吗?
△零存整取储蓄(单利)本利和计算模型: 若每期存入本金 p 元,每期利率为 r,n 期后,本利和为:
△若按复利,如贷款问题——按揭贷款的每期还款计算模型(按揭贷款——分期等额归还本息的借款种类)
若贷款(向银行借款)p 元,采用分期等额还款方式,从借款日算起,一期(如一年)后为第一次还款日,如此下去,
第 n 次还清。如果每期利率为 r(按复利),那么每期应还 x 元,满足
p——贷款数,r——利率,n——还款期数
49. 解排列、组合问题的依据是:分类相加,分步相乘,有序排列,无序组合。
( 2 ) 排 列 : 从 n 个 不 同 元 素 中 , 任 取 m ( m ≤ n ) 个 元 素 , 按 照 一 定 的 顺 序 排 成 一
( 3 ) 组 合 : 从 n 个 不 同 元 素 中 任 取 m ( m ≤ n ) 个 元 素 并 组 成 一 组 , 叫 做 从 n 个 不
50. 解排列与组合问题的规律是:
相邻问题捆绑法;相间隔问题插空法;定位问题优先法;多元问题分类法;至多至少问题间接法;相同元素分组可
采用隔板法,数量不大时可以逐一排出结果。
如:学号为 1,2,3,4 的四名学生的考试成绩
则这四位同学考试成绩的所有可能情况是( ) A. 24 B. 15 C. 12 D. 10
解析:可分成两类:
(2)中间两个分数相等 相同两数分别取 90,91,92,对应的排列可以数出来,分别有
3,4,3 种,∴有 10 种。 ∴共有 5+10=15(种)情况
51. 二项式定理
S a a a a
S a a a a
n n n
n n n
= + + + +
= + + + +
−
−
1 2 1
1 2 1
……
……
相加
(由f x f x
x
x
x
x
x
x x( ) +
= + +
+
= + + + =1
1
1
1 1 1
1
1 1
2
2
2
2
2
2 2
∴原式 = + +
+ +
+ +
f f f f f f f( ) ( ) ( ) ( )1 2 1
2 3 1
3 4 1
4
( 为各类办法中的方法数)mi
分步计数原理: · ……N m m mn= 1 2 ( 为各步骤中的方法数)mi
列,叫做从 个不同元素中取出 个元素的一个排列,所有排列的个数记为n m A n
m .
规定:Cn
0 1=
( )组合数性质:4
( )中间两个分数不相等,1
Cn
r 为二项式系数(区别于该项的系数)
性质:
(3)最值:n 为偶数时,n+1 为奇数,中间一项的二项式系数最大且为第
表示)
52. 你对随机事件之间的关系熟悉吗?
的 和
(并)。
(5)互斥事件(互不相容事件):“A 与 B 不能同时发生”叫做 A、B 互斥。
(6)对立事件(互逆事件):
(7)独立事件:A 发生与否对 B 发生的概率没有影响,这样的两个事件叫做相互独立事件。
53. 对某一事件概率的求法: 分清所求的是:(1)等可能事件的概率(常采用排列组合的方法,即
(5)如果在一次试验中 A 发生的概率是 p,那么在 n 次独立重复试验中 A 恰好发生
如:设 10 件产品中有 4 件次品,6 件正品,求下列事件的概率。
( )( )对称性: , , ,……,1 0 1 2C C r nn
r
n
n r= =− ( )系数和: …2 C C Cn n n
n n0 1 2+ + + =
n C n nn
n
2 1 12+
+项,二项式系数为 ; 为奇数时, 为偶数,中间两项的二项式( )
系数最大即第 项及第 项,其二项式系数为n n C Cn
n
n
n+ + + =
− +1
2
1
2 1
1
2
1
2
( )如:在二项式 的展开式中,系数最小的项系数为 (用数字x −1 11
∴共有 项,中间两项系数的绝对值最大,且为第 或第 项12 12
2 6 7=
由 ,∴取 即第 项系数为负值为最小:C x rr r r
11
11 1 5 6− − =( )
( ) ( )又如: …… ,则1 2 2004
0 1 2
2
2004
2004− = + + + + ∈x a a x a x a x x R
( ) ( ) ( ) ( )a a a a a a a a0 1 0 2 0 3 0 2004+ + + + + + + + =…… (用数字作答)
令 ,得: ……x a a a= + + + =1 10 2 2004 ( )∴原式 …… )= + + + + = × + =2003 2003 1 1 20040 0 1 2004a a a a
( )必然事件 , ,不可能事件 ,1 1 0Ω ΩP P( = =) ( )φ φ
( )包含关系: ,“ 发生必导致 发生”称 包含 。2 A B A B B A⊂
( )事件的和(并): 或 “ 与 至少有一个发生”叫做 与3 A B A B A B A B+
( )事件的积(交): · 或 “ 与 同时发生”叫做 与 的积。4 A B A B A B A B
“ 不发生”叫做 发生的对立(逆)事件,A A A A A A A = =Ω, φ
A B A B A B A B与 独立, 与 , 与 , 与 也相互独立。
P A A m
n( ) = =包含的等可能结果
一次试验的等可能结果的总数
( )( )若 、 互斥,则2 A B P A B P A P B+ = +( ) ( ) ( ) ( ) ( )( )若 、 相互独立,则 · ·3 A B P A B P A P B=
( )4 1P A P A( ) ( )= −
A B
(1)从中任取 2 件都是次品;
(2)从中任取 5 件恰有 2 件次品;
(3)从中有放回地任取 3 件至少有 2 件次品; 解析:有放回地抽取 3 次(每次抽 1 件),∴n=103 而至少有
2 件次品为“恰有 2 次品”和“三件都是次品”
(4)从中依次取 5 件恰有 2 件次品。 解析:∵一件一件抽取(有顺序)
分清(1)、(2)是组合问题,(3)是可重复排列问题,(4)是无重复排列问题。
54.抽样方法主要有:简单随机抽样(抽签法、随机数表法)常常用于总体个数较少时,它的特征是从总体中逐个抽取;
系统抽样,常用于总体个数较多时,它的主要特征是均衡成若干部分,每部分只取一个;分层抽样,主要特征是分层按
比例抽样,主要用于总体中有明显差异,它们的共同特征是每个个体被抽到的概率相等,体现了抽样的客观性和平等性。
55. 对总体分布的估计——用样本的频率作为总体的概率,用样本的期望(平均值)和方差去估计总体的期望和方差。
要熟悉样本频率直方图的作法:
(2)决定组距和组数; (3)决定分点; (4)列频率分布表;
(5)画频率直方图。
如:从 10 名女生与 5 名男生中选 6 名学生参加比赛,如果按性别分层随机抽样,则组成此参赛队的概率为____________。
56. 你对向量的有关概念清楚吗? (1)向量——既有大小又有方向的量。
在此规定下向量可以在平面(或空间)平行移动而不改变。
(6 )并线向量(平行向量)——方向相同或相反的向量。 规定零向量
与任意向量平行。
(7)向量的加、减法如图:
( 8 ) 平 面 向 量 基 本 定 理 ( 向 量 的 分 解 定 理 )
的一组基底。
(9)向量的坐标表示
表示。
∴ · ·P C
3
3
2 2 3
3
4 6 4
10
44
125
= + =
其中,频率 小长方形的面积 组距× 频率
组距
= =
( )样本平均值: ……x n x x x n= + + +1
1 2 ( ) ( ) ( )[ ]样本方差: ……S n x x x x x xn
2
1
2
2
2 21= − + − + + −
( )向量的模——有向线段的长度,2 | |a
→
( )单位向量 ,3 10 0| |
| |
a a a
a
→ →
→
→= =
( )零向量 ,4 0 0 0
→ →
=| | ( )相等的向量 长度相等
方向相同5 ⇔
=
→ →
a b
b a b b a
→ → → → → →
≠ ⇔ =∥ 存在唯一实数 ,使( )0 λ λ
i j x y
→ →
, 是一对互相垂直的单位向量,则有且只有一对实数 , ,使得
( )a x i y j x y a a x y
→ → → → →
= + =,称 , 为向量 的坐标,记作: , ,即为向量的坐标( )
57. 平面向量的数量积
数量积的几何意义:
( 2 ) 数 量 积 的 运 算 法 则
[练习]
答案:
答案:2
答案:
58. 线段的定比分点
※. 你能分清三角形的重心、垂心、外心、内心及其性质吗?
59. 立体几何中平行、垂直关系证明的思路清楚吗? 平行垂直的证明主要利用线面关系的转化:
线 面 平 行 的 判 定 :
线面平行的性质:
三垂线定理(及逆定理):
线面垂直:
( ) · · 叫做向量 与 的数量积(或内积)。1 a b a b a b
→ → → → → →
=| | | |cosθ
a b a b a b
→ → → → →
· 等于 与 在 的方向上的射影 的乘积。| | | |cosθ
注意:数量积不满足结合律 · · · ·( ) ( )a b c a b c
→ → → → → →
≠
( ) ( )( )重要性质:设 , , ,3 1 1 2 2a x y b x y
→ →
= =
② ∥ · · 或 · ·a b a b a b a b a b
→ → → → → → → → → →
⇔ = = −| | | | | | | | ⇔ = ≠
→ → →
a b bλ λ( , 惟一确定)0
( )已知正方形 ,边长为 , , , ,则1 1ABCD AB a BC b AC c
→
=
→
=
→
=
→ → →
( ) ( )( )若向量 , , , ,当 时 与 共线且方向相同2 1 4a x b x x a b
→ → → →
= = =
( )已知 、 均为单位向量,它们的夹角为 ,那么3 60 3a b a bo
→ → → →
+ =| |
( ) ( ) ( )设 , , , ,分点 , ,设 、 是直线 上两点, 点在P x y P x y P x y P P P1 1 1 2 2 2 1 2 l
l 上且不同于 、 ,若存在一实数 ,使 ,则 叫做 分有向线段P P P P PP P1 2 1 2λ λ λ
→
=
→
P P P P P P P P1 2 1 2 1 20 0
→
> <所成的比( , 在线段 内, , 在 外),且λ λ
( ) ( ) ( )如: , , , , , ,∆ABC A x y B x y C x y1 1 2 2 3 3 则 重心 的坐标是 ,∆ABC G x x x y y y1 2 3 1 2 3
3 3
+ + + +
线∥线 线∥面 面∥面
判定 线⊥线 线⊥面 面⊥面 性质
线∥线 线⊥面 面∥面
← → ← →
→ ← → ← → ←
← → ← →
a b b a a∥ , 面 , ∥面⊂ ⊄ ⇒α α α
PA AO PO⊥面 , 为 在 内射影, 面 ,则α α αa ⊂
B
b
O θ
D A
a
a
b
α
α
a
P
O
面面垂直:
60. 三类角的定义及求法
(1)异面直线所成的角θ,0°<θ≤90°
(2)直线与平面所成的角θ,0°≤θ≤90°
(三垂 线定理法:A∈α作或证 AB⊥β于 B,作 BO⊥棱
于 O,连 AO,则 AO⊥棱 l,∴∠AOB 为所求。)
三类 角的求法:
①找出 或作出有关的角。
②证明 其符合定义,并指出所求作的角。
③计算大小(解直角三角形,或用余弦定理)。
[练习]
(1)如图,OA 为α的斜线 OB 为其在α内射影,OC 为α内过 O 点任一直线。
(2)如图,正四棱柱 ABCD—A1B1C1D1 中对角线 BD1=8,BD1 与侧面 B1BCC1 所成
的为 30°。
①求 BD1 和底面 ABCD 所成的角的正弦;
②求异面直线 BD1 和 AD 所成的角;
③求二面角 C1—BD1—B1 的正弦。
(3)如图 ABCD 为菱形,∠DAB=60°,PD⊥面 ABCD,且 PD=AD,求面 PAB 与
面 PCD 所成的锐二面角的大小。
(∵AB∥DC,P 为面 PAB 与面 PCD 的公共点,作 PF∥AB,则 PF 为面 PCD 与面
PAB 的交线……)
61. 空间有几种距离?如何求距离?
点与点,点与线,点与面,线与线,线与面,面与面间距离。
将空间距离转化为两点的距离,构造三角形,解三角形求线段的长(如:三
垂线定理法,或者用等积转化法)。
如:正方形 ABCD—A1B1C1D1 中,棱长为 a,则:
(1)点 C 到面 AB1C1 的距离为___________;
a a⊥面 , 面 ⊥α β β α⊂ ⇒
面 ⊥面 , , , ⊥ ⊥α β α β α β = ⊂ ⇒l la a a
a b a b⊥面 , ⊥面 ∥α α ⇒
面 ⊥ ,面 ⊥ ∥α β α βa a ⇒
( )二面角:二面角 的平面角 ,3 0 180α β θ θ− − < ≤l o o
( 为线面成角,∠ ,∠ )θ γ βAOC = BOC =
);③;②(① 3
6604
3 o
α a
l
β
a
O
α b c
A
O B
γ C
D
α
θ
β
D1 C1
A1 B1
H
G
D C
A B
P F
D C
A E B
(2)点 B 到面 ACB1 的距离为____________;
(3)直线 A1D1 到面 AB1C1 的距离为____________;
(4)面 AB1C 与面 A1DC1 的距离为____________;
(5)点 B 到直线 A1C1 的距离为_____________。
62. 你是否准确理解正棱柱、正棱锥的定义并掌握它们的性质?
正棱柱——底面为正多边形的直棱柱
正棱锥——底面是正多边形,顶点在底面的射影是底面的中心。
正棱锥的计算集中在四个直角三角形中:
它们各包含哪 些元素?
63. 球有哪些性质?
(2)球面上两点的距离是经过这两点的大圆的劣弧长。为此,要找球心角!
(3)如图,θ为纬度角,它是线面成角;α为经度角,它是面面成角。
(5)球内接长方体的对角线是球的直径。正四面体的外接球半径 R 与内切球半径 r 之比为
R:r=3:1。
积为( )
答案:A
64. 熟 记 下 列 公 式 了 吗 ?
( 2 ) 直 线 方 程 :
65. 如何判断两直线平行、垂直?
66. 怎样判断直线 l 与圆 C 的位置关系? 圆心到直线的距离与圆的半径比较。
直线与圆相交时,注意利用圆的“垂径定理”。
67. 怎 样 判 断 直 线 与 圆 锥 曲 线 的 位 置 ?
68. 分清圆锥曲线的定义
Rt SOB Rt SOE Rt BOE Rt SBE∆ ∆ ∆ ∆, , 和
S C h C h正棱锥侧 · ( ——底面周长, 为斜高)= 1
2 ' '
V锥 底面积×高= 1
3
( )球心和截面圆心的连线垂直于截面1 2 2r R d= −
( ) ,球 球4 4 4
3
2 3S R V R= =π π
如:一正四面体的棱长均为 ,四个顶点都在同一球面上,则此球的表面2
A B C D. . . .3 4 3 3 6π π π π
[ )( ) 直线的倾斜角 , , ,1 0 2
2 1
2 1
1 2l α π α α π∈ = = −
− ≠ ≠
k y y
x x x xtan
( ) ( ) ( )P x y P x y a k1 1 1 2 2 2 1, , , 是 上两点,直线 的方向向量 ,l l
→
=
( )点斜式: ( 存在)y y k x x k− = −0 0
斜截式:y kx b= + 截距式: x
a
y
b
+ = 1
一般式: ( 、 不同时为零)Ax By C A B+ + = 0
( )( )点 , 到直线 : 的距离3 00 0
0 0
2 2
P x y Ax By C d Ax By C
A B
l + + = = + +
+
( ) 到 的到角公式:4 11 2
2 1
1 2
l l tanθ = −
−
k k
k k l l1 2
2 1
1 21
与 的夹角公式: tanθ = −
−
k k
k k
A B A B
A C A C
1 2 2 1
1 2 2 1
1 2
=
≠
⇔ l l∥ k k l1 2 1 2= ⇒ l ∥ (反之不一定成立)
A A B B1 2 1 2 1 20+ = ⇔ l l⊥
联立方程组 关于 (或 )的一元二次方程 “ ”
相交; 相切; 相离
⇒ ⇒
> ⇔ = ⇔ < ⇔
x y ∆
∆ ∆ ∆0 0 0
第一定义
椭圆 ,
双曲线 ,
抛物线
⇔ + = > =
⇔ − = < =
⇔ =
PF PF a a c F F
PF PF a a c F F
PF PK
1 2 1 2
1 2 1 2
2 2 2
2 2 2
第二定义:e PF
PK
c
a
= =
D C
A B
D1 C1
A1 B1
y
b
O
F1 F2 a x
x a
c
=
2
F
k
e>1 e=1
0 ⇔ = ⇔e e e椭圆; 双曲线; 抛物线
( )69 1 0
2
2
2
2
2
2
2
2. 与双曲线 有相同焦点的双曲线系为x
a
y
b
x
a
y
b
− = − = ≠λ λ
( ) ( )[ ]弦长公式 P P k x x x x1 2
2
1 2
2
1 21 4= + + − ( )[ ]= +
+ −1 1 42 1 2
2
1 2k y y y y
如:椭圆 与直线 交于 、 两点,原点与 中点连mx ny y x M N MN2 2 1 1+ = = −
线的斜率为 ,则 的值为2
2
m
n
(由 , , )a x x b y y x a x y b y= + = + ⇒ = − = −' ' ' '2 2 2 2
( )只要证明 , 也在曲线 上,即A a x b y C f x y' ( ') '2 2− − =
( )点 、 关于直线 对称 ⊥
中点在 上2 A A AA
AA
' '
'
l l
l
⇔
⇔ = −
k k
AA
AA'
'
·
中点坐标满足 方程
l
l
1
74 2 2 2. cos
sin
圆 的参数方程为 ( 为参数)x y r x r
y r
+ = =
=
θ
θ θ 椭圆 的参数方程为 ( 为参数)x
a
y
b
x a
y b
2
2
2
2 1+ = =
=
cos
sin
θ
θ θ
y
P(x0,y0)
K
F1 O F2 x
l
y
A P2
O F x
P1 B