人教版九年级数学上册同步测试题课件（4）

人教版九年级数学上册同步测试题课件（4）

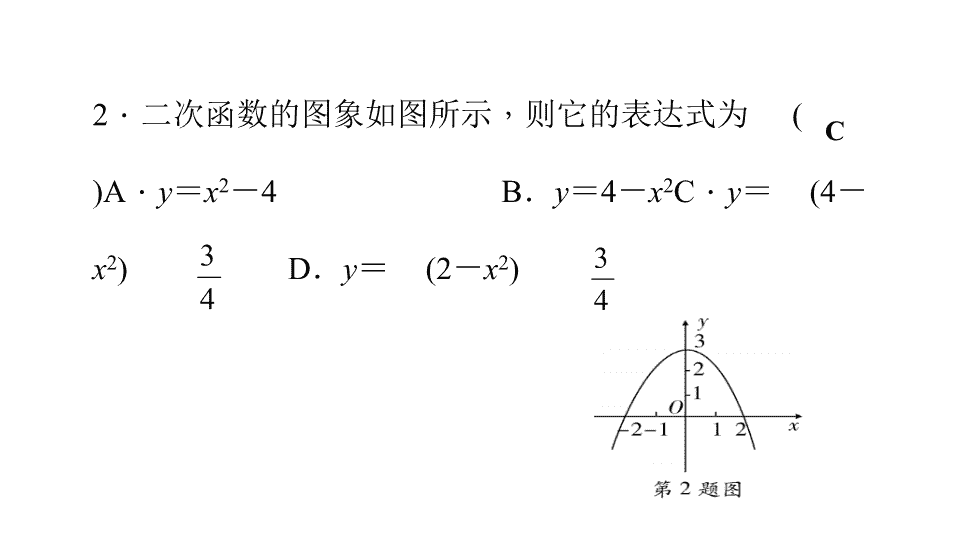
周周测 ( 四 )(22.1.4 ～ 22.2) 时间： 45 分钟　满分： 100 分　姓名： ________ 一、选择题 ( 每小题 3 分 ， 共 24 分 ) 1 ． 函数 y ＝ x 2 ＋ 3 x － 1 的对称轴是 （ ） A ． x ＝ B ． x ＝－ C ． x ＝－ D ． x ＝－ C C 2 ． 二次函数的图象如图所示 ， 则它的表达式为 ( ) A ． y ＝ x 2 － 4 B ． y ＝ 4 － x 2 C ． y ＝ (4 － x 2 ) D ． y ＝ (2 － x 2 ) 3 ． 已知抛物线 y ＝－ 2 x 2 ＋ 12 x － 13 ， 则下列关于此抛物线说法正确的是 ( 　　 ) A ． 开口向下 ， 对称轴为直线 x ＝－ 3 B ． 顶点坐标为 ( － 3 ， 5 ) C ． 最小值为 5 D ． 当 x ＞ 3 时 ， y 随 x 的增大而减小 D 4 ． ( 临沂中考 ) 要将抛物线 y ＝ x 2 ＋ 2 x ＋ 3 平移后得到抛物线 y ＝ x 2 ， 下列平移方法正确的是 ( 　　 ) A ． 向左平移 1 个单位 ， 再向上平移 2 个单位 B ． 向左平移 1 个单位 ， 再向下平移 2 个单位 C ． 向右平移 1 个单位 ， 再向上平移 2 个单位 D ． 向右平移 1 个单位 ， 再向下平移 2 个单位 D C 5 ． 抛物线 y ＝ ax 2 ＋ bx ＋ c ( a ＜ 0) 如图所示 ， 则关于 x 的不等式 ax 2 ＋ bx ＋ c ＞ 0 的解集是 ( 　　 ) A ． x ＜ 2 B ． x ＞－ 3 C ． － 3 ＜ x ＜ 1 D ． x ＜－ 3 或 x ＞ 1 6 ． ( 随州中考 ) 对于二次函数 y ＝ x 2 － 2 mx － 3 ， 下列结论错误的是 ( 　　 ) A ． 它的图象与 x 轴有两个交点 B ． 方程 x 2 － 2 mx ＝ 3 的两根之积为－ 3 C ． 它的图象的对称轴在 y 轴的右侧 D ． x ＜ m 时 ， y 随 x 的增大而减小 C 7 ． ★ ( 兰州中考 ) 二次函数 y ＝ ax 2 ＋ bx ＋ c 的图 象如图 ， 点 C 在 y 轴的正半轴上 ， 且 OA ＝ OC ， 则 ( 　　 ) A ． ac ＋ 1 ＝ b B ． ab ＋ 1 ＝ c C ． bc ＋ 1 ＝ a D ．以上都不是 A A 8 ． ★ ( 南宁中考 ) 二次函数 y ＝ ax 2 ＋ bx ＋ c ( a ≠ 0) 和 正比例函数 y ＝ x 的图象如图所示 ， 则方程 ax 2 ＋ ＋ c ＝ 0( a ≠ 0) 的两根之和 ( 　 　 ) A ． 大于 0 B ．等于 0 C ． 小于 0 D ．不能确定 直线 X=2 (2 ，－ 2) 二、填空题 ( 每小题 4 分 ， 共 24 分 ) 9 ． 二次函数 y ＝ 2( x － 1)( x － 3) 的对称轴是 ， 顶点坐标是 10 ． ( 杭州中考 ) 函数 y ＝ x 2 ＋ 2 x ＋ 1 ， 当 y ＝ 0 时 ， x ＝ ；当 1 ＜ x ＜ 2 时 ， y 随 x 的增大而 填 “ 增大 ” 或 “ 减小 ” ) ． 增大 － 1 11．若抛物线 与x轴没有交点，则m的取值范围是 . 12．若二次函数 图象的最低点的坐标为(1，－1)，则关于x的一元二次方程 的根为 . 13 ． 抛物线 y ＝－ x 2 ＋ 2 x － 3 关于 x 轴对称的抛物线的解析式是 . 14．★抛物线y＝ax2＋bx＋c上部分点的横坐标x，纵坐标y的对应值如下表： 则下列说法中正确的是 .(填写序号) ① 抛物线与 x 轴的一个交点为 (3 ， 0 ) ； ② 函数 y ＝ ax 2 ＋ bx ＋ c 的最大值为 6 ； ③ 抛物线的对称轴是 x ＝ 0.5 ； ④ 在对称轴左侧 ， y 随 x 的增大而增大． 三、解答题 ( 共 52 分 ) 15 ． (12 分 ) 如图 ， 抛物线 y ＝－ x 2 ＋ ( m － 1) x ＋ m 与 y 轴交于点 (0 ， 3 ) ． (1) 求出 m 的值 ， 并画出这条抛物线； (2) 求抛物线与 x 轴的交点和顶点坐 标； ( 3) 当 x 取什么值时 ， 抛物线在 x 轴上方？ (4) 当 x 取什么值时 ， y 的值随 x 的增大而减小？ ( 2 ) 抛物线与 x 轴的交点为 ( － 1 ， 0 ) ， ( 3 ， 0 ) ， 顶点坐标为 ( 1 ， 4 ) ． 解： ( 1 ) ∵ 抛物线 y ＝－ x 2 ＋ ( m － 1 ) x ＋ m 与 y 轴交点 ( 0 3 ) ， ∴ m ＝ 3. 图象如图所示 ． ( 3 ) 当－ 1 ＜ x ＜ 3 时 ， 抛物线在 x 轴上方 ( 4 ) 当 x ＞ 1 时 ， y 的值随 x 的增大而减小． 16 ． (12 分 ) ( 南京中考 ) 已知函数 y ＝－ x 2 ＋ ( m － 1) x ＋ m ( m 为常数 ) ． (1) 该函数的图象与 x 轴公共点的个数是 ______ ． A ． 0 　 B ． 1 　 C ． 2 D ． 1 或 2 (2) 求证：不论 m 为何值 ， 该函数的图象的顶点都在函数 y ＝ ( x ＋ 1) 2 的图象上． 解： ( 1 ) ∵ 函数 y ＝－ x 2 ＋ ( m － 1 ) x ＋ m ( m 为常数 ) ， ∴ Δ ＝ ( m － 1 ) 2 ＋ 4m ＝ ( m ＋ 1 ) 2 ≥ 0 ， 则该函数图象与 x 轴的公共点的个数是 1 或 2 ， 故选 ； D ( 2 ) y ＝－ x 2 ＋ ( m － 1 ) x ＋ m ＝ －（ x － ） + ， 把 x ＝ 代入 y ＝ ( x ＋ 1 ) 2 得 y=( +1 ) 2 = . 则不论 m 为何值 ， 该函数的图象的顶点都在函数 y ＝ ( x ＋ 1 ) 2 的图象上． 17 ． (12 分 ) ( 龙东中考 ) 如图 ， 抛物线 y ＝ x 2 － bx ＋ c 交 x 轴于点 A (1 ， 0 ) ， 交 y 轴于点 B . (1) 求抛物线的解析 式； ( 2) 点 P 是抛物线对称轴上的一个动点 ， 是否存在点 P ， 使 △ PAB 的周长最小？若存在 ， 求出点 P 的坐标；若不存在 ， 请说明理由． ( 2 ) 连接 BC ， BC 与对称轴的交点就是所要求的点 P ， 设 BC 的解析式为 y ＝ kx ＋ b ( k ≠ 0 ) ， 根据题意： b＝3 b＝3 3k＋b＝0 解得 k＝－1 　 ∴ y ＝－ x ＋ 3 ， 当 x ＝ 2 时 ， y ＝ 1 ， ∴ P ( 2 ， 1 ) ． { { 解： ( 1 ) 根据题意得 C ( 3 ， 0 ) ， 9-3b+c=0 , b=4, 1-b+c=0 , 解得 c=3. 所以二次函数的解析式为 y ＝ x 2 － 4x ＋ 3. { { 18 ． (16 分 ) ( 黑龙江中考 ) 如图 ， 已知抛物线 y ＝－ x 2 ＋ mx ＋ 3 与 x 轴交于点 A ， B 两点 ， 与 y 轴 交于 C 点 ， 点 B 的坐标为 (3 ， 0 ) ， 抛物线与直线 y ＝－ x ＋ 3 交于 C ， D 两点 ， 连接 BD ， AD . (1) 求 m 的值． (2) 抛物线上有一点 P ， 满足 S △ ABP ＝ 4 S △ ABD ， 求点 P 的坐标． 解： ( 1 ) ∵ 抛物线 y ＝－ x 2 ＋ mx ＋ 3 过 ( 3 ， 0 ) ， ∴ 0 ＝－ 9 ＋ 3m ＋ 3 ， ∴ m ＝ 2