高考数学必考必背公式全集

高考数学必考必背公式全集

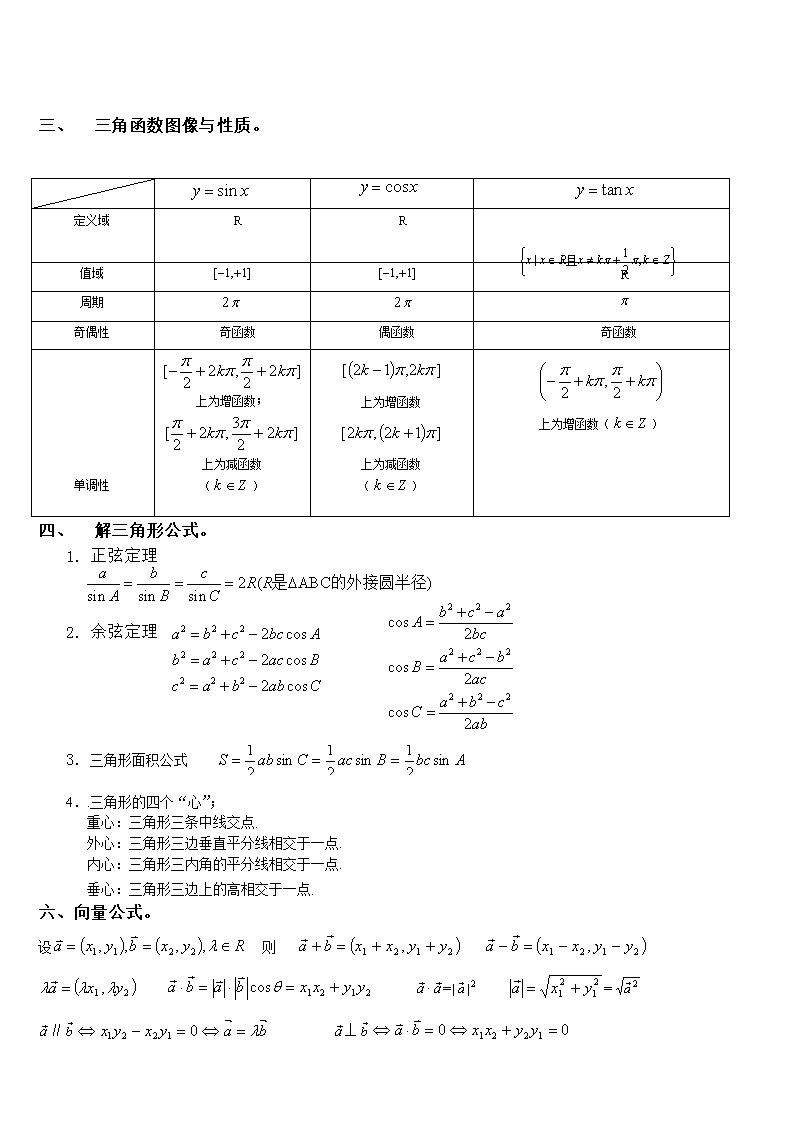
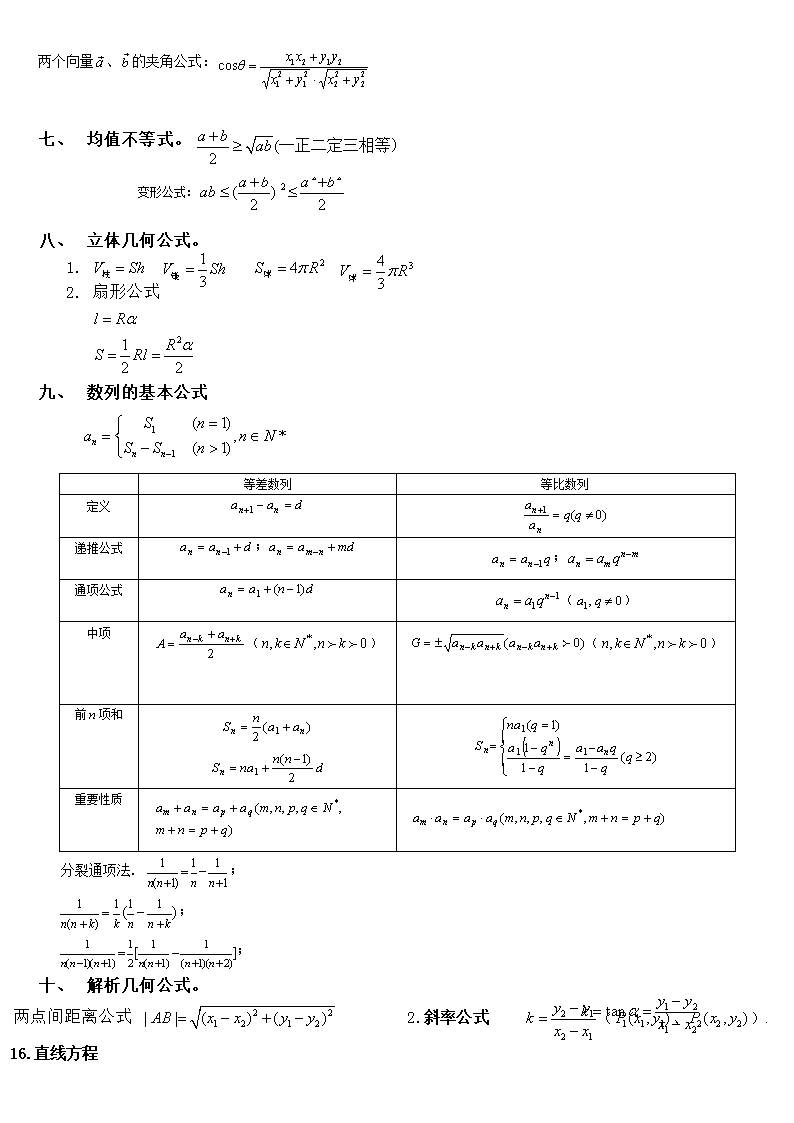
一、 对数运算公式。‎ ‎1. 2. 3. 4. ‎ ‎5. 6. 7. ‎ ‎8. 9. 10. ‎ ‎ ‎ 二、 三角函数运算公式。‎ 1. 同角关系: ‎ 2. 诱导公式：奇变偶不变，符号看象限。‎ ‎ ‎ ‎ ‎ 3. 两角和差公式: ‎ ‎ ‎ ‎ 二倍角公式: ‎ ‎ ‎ 4. 辅助角公式：，其中，‎ 5. 降幂公式（二倍角余弦变形）: ‎ ‎6.角函数定义：角中边上任意一点为，设则：‎ 一、 三角函数图像与性质。‎ 二、 解三角形公式。‎ 定义域 R R 值域 R 周期 奇偶性 奇函数 偶函数 奇函数 单调性 ‎ 上为增函数；上为减函数 ‎（）‎ 上为增函数 上为减函数 ‎（）‎ 上为增函数（）‎ 1. 正弦定理 ‎ ‎ 2. 余弦定理 3. 三角形面积公式 ‎ ‎4．.三角形的四个“心”；‎ 重心：三角形三条中线交点.‎ 外心：三角形三边垂直平分线相交于一点.‎ 内心：三角形三内角的平分线相交于一点.‎ 垂心：三角形三边上的高相交于一点.‎ 六、向量公式。‎ 设 则 ‎ ‎ ·= = ‎ ‎∥ ⊥ ‎ 两个向量、的夹角公式：‎ 七、 均值不等式。 ‎ 变形公式：‎ 八、 立体几何公式。‎ ‎1. ‎ ‎2. 扇形公式 ‎ ‎ 九、 数列的基本公式 等差数列 等比数列 定义 递推公式 ‎；‎ ‎；‎ 通项公式 ‎（）‎ 中项 ‎（）‎ ‎（）‎ 前项和 重要性质 分裂通项法. ；‎ ‎；‎ ‎；‎ 十、 解析几何公式。‎ 两点间距离公式 2.斜率公式 （、）.‎ ‎16.直线方程 ‎ ‎（1）点斜式 (直线过点，且斜率为)．‎ ‎（2）斜截式 (b为直线在y轴上的截距).‎ ‎（3）一般式 (其中A、B不同时为0).‎ 1. 两点间距离公式 ‎3.点到直线距离公式 4.平行线间距离公式 圆的四种方程 ‎（1）圆的标准方程 .‎ ‎（2）圆的一般方程 (＞0).‎ ‎19.点与圆的位置关系 点与圆的位置关系有三种 若，则 点在圆外;点在圆上;点在圆内.‎ ‎ 函数在点处的导数的几何意义 函数在点处的导数是曲线在处的切线的斜率，相应的切线方程是.‎ 十一.圆锥曲线方程 1. 椭圆： ①方程(a>b>0); ②定义: |PF1|+|PF2|=‎2a>‎2c； ③ e= ④长轴长为‎2a，短轴长为2b； ⑤a2=b2+c2 ；‎ ‎⑥=‎ ‎2.双曲线 ：①方程(a,b>0)；②定义: ||PF1|-|PF2||=‎2a<‎2c； ③e=,c2=a2+b2； ④= ⑧渐进线或; ‎ ‎3.抛物线 ①方程y2=2px ； ②定义:|PF|=d准；③顶点为焦点到准线垂线段中点;x,y范围?轴？焦点F(,0),准线x=-,‎ ‎④焦半径; 焦点弦＝x1+x2+p; y1y2=－p2, x1x2=其中A(x1,y1)、B(x2,y2) ⑤通径2p,焦准距p;‎ ‎4.弦长公式：；‎ ‎5过两点椭圆、双曲线标准方程可设为： （同时大于0时表示椭圆，时表示双曲线）；‎ 十二求导公式及运算法则。‎ ‎1. 2. 3. 4. ‎ ‎5. 6. 7. 8. 9. 10. 11. ‎ ‎12. ‎ 曲线在点处切线的斜率k＝f/(x0)表示过曲线y=f(x)上P(x0,f(x0))切线斜率。‎ ① ‎ 十三.复数的相等 .（）‎ 复数的模（或绝对值） ==.‎ ‎ 十四。 方差 去估计总体方差。⑶样本标准差=25（理科）、‎ ‎3.(理科)排列数公式:, .‎ 组合数公式：,.‎ 组合数性质：；.‎ ‎4. (理科)二项式定理：‎ ‎ ⑴掌握二项展开式的通项：；‎ ‎⑵注意第r＋1项二项式系数与第r＋1项系数的区别.‎ 异面直线所成角 ‎=‎ ‎（其中（）为异面直线所成角，分别表示异面直线的方向向量）‎ ‎26、直线与平面所成角(为平面的法向量).‎ ‎27、.二面角的平面角 或（，为平面，的法向量）.‎ ‎28、.点到平面的距离 ‎ ‎（为平面的法向量，是经过面的一条斜线，）.‎ 基本的积分公式：＝C；＝＋C（m∈Q， m≠－1）；dx＝ln＋C；＝＋C；＝＋C；＝sinx＋C；＝－cosx＋C（表中C均为常数）‎ ‎5．(理科)离散性随机变量的分布列 一般地，设离散型随机变量可能取得值为：‎ ‎ X1，X2，…，X3，…，‎ 取每一个值Xi（I=1，2，…）的概率为P（，则称表 X1‎ X2‎ ‎…‎ xi ‎…‎ P P1‎ P2‎ ‎…‎ Pi ‎…‎ 为随机变量的概率分布，简称的分布列。‎ 两条基本性质：①…)；②P1+P2+…=1。‎ ‎6．独立重复试验：若n次重复试验中，每次试验结果的概率都不依赖于其他各次试验的结果，则称这n次试验是独立的。‎ ‎ (1)两个相互独立事件同时发生的概率，等于每个事件发生的概率的积，即P（A·B）=P（A）·P（B）；‎ ‎ (2)如果在一次试验中某事件发生的概率为P,那么在n次独立重复试验中这个事件恰好发生k次的概率：Pn(k)=CPk(1－P)n-k。‎ ‎7．随机变量的均值和方差 ‎（1）随机变量的均值…；反映随机变量取值的平均水平。‎ ‎（2）离散型随机变量的方差：……；反映随机变量取值的稳定与波动，集中与离散的程度。‎ ‎　　基本性质：；。‎ ‎8．几种特殊的分布列 ‎（1）两点分布：对于一个随机试验，如果它的结果只有两种情况，则我们可用随机变量，来描述这个随机试验的结果。如果甲结果发生的概率为P，则乙结果发生的概率必定为1－P，均值为E=p，方差为D=p（1－p）。‎ ‎（2）超几何分布:重复进行独立试验，每次试验只有成功、失败两种可能，如果每次试验成功的概率为p，重复试验直到出现一次成功为止，则需要的试验次数是一个随机变量，用ξ表示，因此事件{ξ＝n}表示“第n次试验成功且前n－1次试验均失败”。所以，其分布列为：‎ ξ ‎1‎ ‎2‎ ‎…‎ n ‎…‎ P p p(1－p)‎ ‎…‎ ‎…‎ ‎（3）二项分布:如果我们设在每次试验中成功的概率都为P，则在n次重复试验中，试验成功的次数是一个随机变量，用ξ来表示，则ξ服从二项分布．则在n次试验中恰好成功k次的概率为：‎ 记ε是n次独立重复试验某事件发生的次数，则ε～B（n，p）；‎ 其概率…。期望Eε=np，方差Dε=npq。‎ ‎9．正态分布:正态分布密度函数：，均值为Eε=μ，方差为。‎ 正态曲线具有以下性质：‎ ‎（1）曲线在x轴的上方，与x轴不相交。‎ ‎（2）曲线关于直线x =μ对称。‎ ‎（3）曲线在x =μ时位于最高点。‎ ‎（4）当x <μ时，曲线上升；当x >μ时，曲线下降。并且当曲线向左、右两边无限延伸时，以x轴为渐近线，向它无限靠近。‎ ‎（5）当μ一定时，曲线的形状由σ确定。σ越大，曲线越“矮胖”，表示总体越分散；σ越小，曲线越“瘦高”，表示总体的分布越集中。‎ 十三、参数极坐标 ‎1.极坐标：M是平面上一点，表示OM的长度，是，‎ 则有序实数实数对,叫极径，叫极角；一般地，，。‎ ‎2.极坐标和直角坐标互化公式 ‎ 或 ，θ的象限由点(x,y)所在象限确定.‎ ‎（1）它们互化的条件则是：极点与原点重合，极轴与x轴正半轴重合. ‎ ‎（2）将点变成直角坐标，也可以根据几何意义和三角函数的定义获得。 ‎