- 2021-04-14 发布 |
- 37.5 KB |
- 9页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2019-2020学年江西省南昌市第二中学高二上学期期末考试数学(文)试题
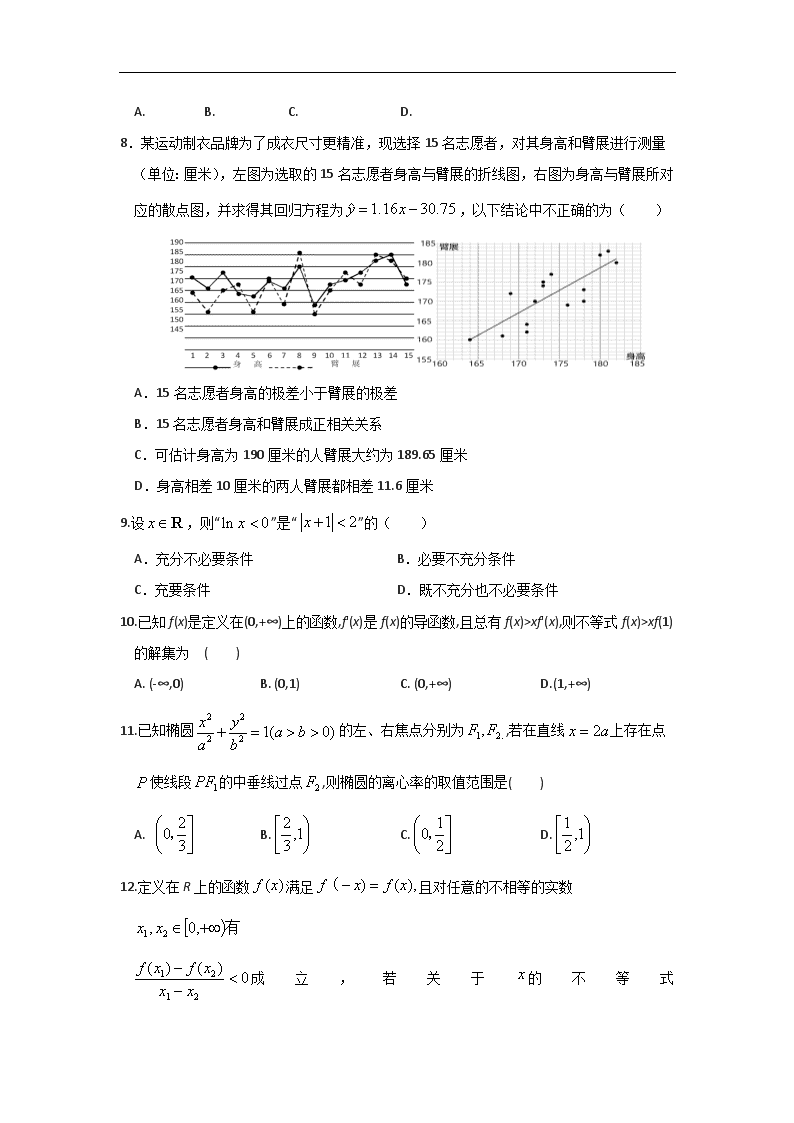
南昌二中2019—2020学年度上学期期末考试 高二数学(文)试卷 一、选择题(每小题5分,共12小题,共60分) 1.已知复数z满足z(1+i)=2﹣i,则复数z在复平面内对应的点所在象限为( ) A.第一象限 B.第二象限 C.第三象限 D.第四象限 2.下列关于命题的说法错误的是( ) A.命题“若x2﹣3x+2=0,则x=2”的逆否命题为“若x≠2,则x2﹣3x+2≠0” B.“a=2”是“函数f(x)=ax在区间(﹣∞,+∞)上为增函数”的充分不必要条件 C.命题“∃x∈R,使得x2+x+1<0”的否定是:“∀x∈R,均有x2+x+1≥0” D.“若f ′(xo)=0,则xo为y=f(x)的极值点”为真命题 3.双曲线的离心率为,则其渐近线方程为 A. B. C. D. 4.吸烟有害健康,远离烟草,珍惜生命. 据统计一小时内吸烟5支诱发脑血管病的概率为0.02,一小时内吸烟10支诱发脑血管病的概率为0.16.已知某公司职员在某一小时内吸烟5支未诱发脑血管病,则他在这一小时内还能继吸烟5支不诱发脑血管病的概率为( ) A. B. C. D.不确定 5.已知椭圆C:1(a>b>0)的离心率为,且椭圆C的长轴长与焦距之和为6,则椭圆C的标准方程为( ) A.1 B. C.1 D. 6.下面四个推理,不属于演绎推理的是( ) A. 函数的值域为[−1,1],因为,所以的值域也为[−1,1] B. 昆虫都是6条腿,竹节虫是昆虫,所以竹节虫有6条腿 C. 在平面中,对于三条不同的直线a,b,c,若a∥b,b∥c则a∥c,将此结论放到空间中也是如此 D. 如果一个人在墙上写字的位置与他的视线平行,那么墙上字迹离地的高度大约是他的身高,凶手在墙上写字的位置与他的视线平行,福尔摩斯量得墙壁上的字迹距地面六尺多,于是,他得出了凶手身高六尺多的结论 7.函数f(x)=x3-x2+mx+1不是R上的单调函数,则实数m的取值范围是 ( ) A. B. C. D. 8.某运动制衣品牌为了成衣尺寸更精准,现选择15名志愿者,对其身高和臂展进行测量(单位:厘米),左图为选取的15名志愿者身高与臂展的折线图,右图为身高与臂展所对应的散点图,并求得其回归方程为,以下结论中不正确的为( ) A.15名志愿者身高的极差小于臂展的极差 B.15名志愿者身高和臂展成正相关关系 C.可估计身高为190厘米的人臂展大约为189.65厘米 D.身高相差10厘米的两人臂展都相差11.6厘米 9.设,则“”是“”的( ) A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要条件 10.已知f(x)是定义在(0,+∞)上的函数,f'(x)是f(x)的导函数,且总有f(x)>xf'(x),则不等式f(x)>xf(1)的解集为 ( ) A. (-∞,0) B. (0,1) C. (0,+∞) D.(1,+∞) 11.已知椭圆的左、右焦点分别为,若在直线上存在点使线段的中垂线过点,则椭圆的离心率的取值范围是( ) A. B. C. D. 12.定义在R上的函数满足且对任意的不相等的实数 成立,若关于的不等式 在上恒成立,则实数m的取值范围是( ) A. B. C. D. 二、填空题(每小题5分,共20分) 13.已知实数x,y满足不等式组,则z=2x﹣3y的最小值为 . 14.在平面直角坐标系中,点在曲线(为自然对数的底数)上,且该曲线在点 处的切线经过原点,则点的坐标是______. 15.斜率为的直线过双曲线的左焦点F1与双曲线的右支交于点P,且PF2与x轴垂直(F2为右焦点),则此双曲线的离心率为 . 16.已知函数f(x)的导函数f'(x)是二次函数,且y=f'(x)的图像关于y轴对称,f'(3)=0,若f(x)的极 大值与极小值之和为4,则f(0)= . 三、解答题(共5小题,共60分) 17.(本小题12分) 已知命题p:关于x的方程在上有实根;命题q:方程表示的曲线是焦点在x轴上的椭圆. (I)若p是真命题,求a的取值范围; (II)若是真命题,求a的取值范围. 18. (本小题12分) 2019年初,某市为了实现教育资源公平,办人民满意的教育,准备在今年8月份的小升初录取中在某重点中学实行分数和摇号相结合的录取办法.该市教育管理部门为了了解市民对该招生办法的赞同情况,随机采访了440名市民,将他们的意见和是否近三年家里有小升初学生的情况进行了统计,得到如下的2×2列联表. 赞同录取办法人数 不赞同录取办法人数 合计 近三年家里没有小升初学生 180 40 220 近三年家里有小升初学生 140 80 220 合计 320 120 440 (I)根据上面的列联表判断,能否在犯错误的概率不超过0.001的前提下认为是否赞同小升初录取办法与近三年是否家里有小升初学生有关; (II)从上述调查的不赞同小升初录取办法人员中根据近三年家里是否有小升初学生按分层抽样抽出6人,再从这6人中随机抽出3人进行电话回访,求3人中恰有1人近三年家里没有小升初学生的概率. 附:,其中. P() 0.10 0.05 0. 025 0.10 0.005 0.001 2.706 3.841 5.024 6.635 7.879 10.828 18. (本小题12分) 已知函数f(x)=x2+2alnx. (I)若函数f(x)的图象在(2,f(2))处的切线斜率为1,求实数a的值; (II)若函数在[1,2]上是减函数,求实数a的取值范围. 19. (本小题12分) 已知点F是抛物线C:y2=2px(p>0)的焦点,若点P(x0,4)在抛物线C上,且. (I)求抛物线C的方程; (II)动直线l:x=my+1(m∈R)与抛物线C相交于A,B两点,问:在x轴上是否存在定点其中D(t,0)(其中t≠0),使得kAD+kBD=0?(kAD,kBD分别为直线AD,BD的斜率)若存在,求出点D的坐标;若不存在,请说明理由. 18. (本小题12分) 已知函数f(x)=-ln x. (I)求f(x)的最小值; (II)若关于x的不等式ex-1+1-f(x)>在(1,+∞)上恒成立,求整数k的最大值. 四、选做题(共10分) 22.在平面直角坐标系中,曲线的参数方程为(为参数).以O为极点,轴的正半轴为极轴建立极坐标系. (I)写出的极坐标方程; (II)设曲线经伸缩变换后得到曲线C3,曲线分别与和交于,两点,求. 23.已知函数. (Ⅰ)求不等式的解集; (Ⅱ)若的解集非空,求的取值范围. 高二数学(文)期末考试参考答案 1.D 2.D 3.A 4.A 5.B 6.C 7.C 8.D 9.A 10.B 11.B 12、D 13.-6 14. 15.e. 16. 2 17.令, 则, 当时,,在上单调递减, 当时,,在上单调递增, 的最小值, 故若p为真命题,则; 是真命题,则p,q均为真命题, q为真命题,即方程表示的曲线是焦点在x轴上的椭圆, 则, 由知,p为真命题时, 所以是真命题,则. 18.(1)假设是否赞同小升初录取办法与近三年是否有家里小升初学生无关,的观测,因为 所以能在犯错误概率不超过0.001的前提下认为是否赞同小升初录取办法与近三年是否家里有小升初学生有关. (2)设从近三年家里没有小升初学生的人员中抽出人,从近三年家里有小升初学生的人员中抽出人,由分层抽样的定义可知,解得,. 设事件M为3人中恰有1人近三年家里没有小升初学生.在抽出的6人中,近三年家里没有小升初学生的2人,分别记为,,近三年家里有小升初学生的4人,分别记为,,,,则从这6人中随机抽出3人有20种不同的抽法,所有的情况如下: {,,},{,,},{,,},{,,},{,,},{,,},{,,},{,,},{,,},{,,},{,,},{, ,},{,,},{,,},{,,},{,,},{,,},{,,},{,,},{,,}. 其中恰有1人近三年家里没有小升初学生的情况有12种,分别为: {,,},{,,},{,,},{,,},{,,},{,,},{,,},{,,},{,,},{,,},{,,},{,,}, 所以3人中恰有1人近三年家里没有小升初学生的概率为. 19.(1) 由已知f'(2)=1,解得a=﹣3.… (2)由得,… 由已知函数g(x)为[1,2]上的单调减函数, 则g'(x)≤0在[1,2]上恒成立, 即在[1,2]上恒成立. 即在[1,2]上恒成立. 令,在[1,2]上, 所以h(x)在[1,2]为减函数., 所以. 20.(1)由题意得:抛物线的准线方程:x,∵点P(x0,4)在抛物线C上,∴42=2px0,所以x0, 所以|PF|=x0﹣(),所以由题意:p (p>0),解得:p=2, 所以抛物线C的方程:y2=4x; (2)由题意得m≠0,假设存在D(t,0)使得kAD+kBD=0,设A(x,y),B(x',y'),整理得: y2﹣4mx﹣4=0,∴y+y'=4m,yy'=﹣4,kAD, kBD,由kAD+kBD=0得:0⇒2myy'+(1﹣t)•(y+y')=0⇒ 2m(﹣4)+(1﹣t)4m=0⇒m(﹣1﹣t)=0,m≠0∴t=﹣1时,使得kAD+kBD=0, 即D点的坐标:(﹣1,0). 21.(1)由(1)知f'(x)=ex-1-. 当x>1时,f'(x)>0;当0查看更多
- 当前文档收益归属上传用户
- 下载本文档