- 2021-04-14 发布 |
- 37.5 KB |
- 37页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
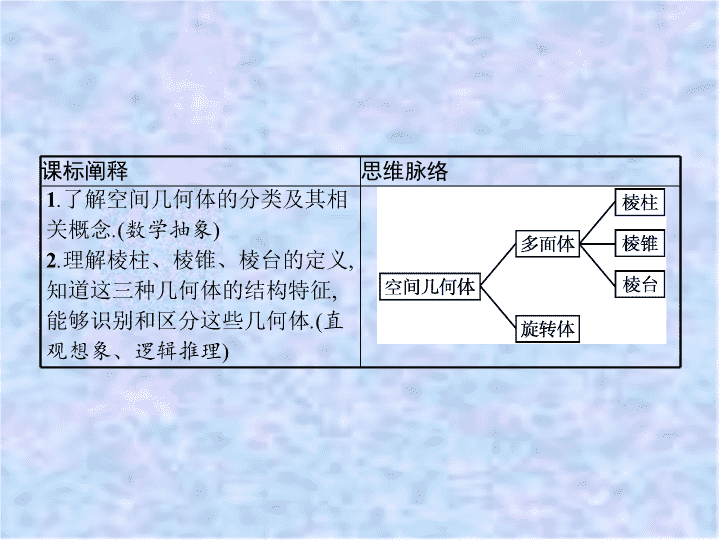
【新教材】2020-2021学年高中人教A版数学必修第二册课件:8-1 第1课时 棱柱、棱锥、棱台的结构特征
第 1 课时 棱柱、棱锥、棱台的结构特征 课标阐释 思维脉络 1 . 了解空间几何体的分类及其相关概念 . ( 数学抽象 ) 2 . 理解棱柱、棱锥、棱台的定义 , 知道这三种几何体的结构特征 , 能够识别和区分这些几何体 . ( 直观想象、逻辑推理 ) 激趣诱思 知识点拨 金字塔 , 阿拉伯文意为 “ 方锥体 ”, 它是一种方底、尖顶的石砌建筑物 , 是古代埃及埋葬国王、王后或王室其他成员的陵墓 . 它既不是金子做的 , 也不是我们通常所见的宝塔形 , 而是由于它规模宏大 , 从四面看都呈等腰三角形 , 很像汉语中的 “ 金 ” 字 , 故中文形象地把它译为 “ 金字塔 ” . 在四千多年前生产工具落后的中古时代 , 埃及人是怎样采集、搬运数量如此之多 , 每块又如此之重的巨石 , 垒成如此宏伟的大金字塔的 ? 这真是一个十分难解的谜 . 激趣诱思 知识点拨 知识点一、空间几何体的定义、分类与相关概念 1 . 空间几何体 : 如果只考虑物体的 形状 和 大小 , 而不考虑其他因素 , 那么由这些物体抽象出来的 空间图形 就叫做空间几何体 . 2 . 分类 : 常见的空间几何体有 多面体 和 旋转体 两类 . 3 . 多面体和旋转体 类别 多面体 旋转体 定义 一般地 , 由若干 个 平面 多边形 围成的几何体叫做多面体 ④ 一条 平面曲线 ( 包括直线 ) 绕它所在平面内的一条定直线旋转所形成的 曲面 叫做旋转面 . ⑤ 封闭 的旋转面围成的几何体叫做旋转体 激趣诱思 知识点拨 类别 多面体 旋转体 图形 相关 概念 ① 面 : 围成多面体的各个 多边形 叫做多面体的面 . ② 棱 : 两个面的 公共边 叫做多面体的棱 . ③ 顶点 : 棱与棱的 公共点 叫做多面体的顶点 轴 : 形成旋转面所绕 的 定 直线 叫做旋转体的轴 激趣诱思 知识点拨 微思考 观察下列图片 , 这些都是我们日常熟知的一些物体 : (1) 哪些物体围成它们的每个面都是平面图形 , 并且都是平面多边形 ? 提示 : ②④ . (2) 哪些物体围成它们的面中既有平面图形 , 又有曲面图形 ? 提示 : ①③⑤ . (3) 哪些物体围成它们的面都是曲面图形 ? 提示 : ⑥ . 激趣诱思 知识点拨 知识点二、棱柱的结构特征 1 . 棱 柱 图形及表示 定义 一般地 , 有两个面 互相平行 , 其余各面 都是 四边形 , 并且相邻两个四边形的公共 边都 互相 平行 , 由这些面所围成的多面体叫做棱柱 用表示底面各顶点的字母表示 . 如图棱柱可记作 : 棱柱 ABCDEF-A'B'C'D'E'F' 相关 概念 底面 : 两个互相 平行 的面叫做棱柱的底面 ; 侧面 : 其余各面 叫做棱柱的侧面 ; 侧棱 : 相邻侧面的 公共边 叫做棱柱的侧棱 ; 顶点 : 侧面与底面 的公共顶点叫做棱柱的顶点 分类 ① 依据 : 底面多边形的 边数 ; ② 举例 : 三棱柱 ( 底面是三角形 ) 、 四棱柱 ( 底面是四边形 )…… 激趣诱思 知识点拨 2 . 棱柱的 分类 3 . 常见的几种四棱柱之间的转化 关系 名师点析 棱柱的结构特征包括两个方面 : 一是面 , 二是棱 . 棱柱的面共有两种 : 第一种是底面 , 上、下共两个底面而且是平行且全等的 ; 第二种是侧面 , 几棱柱就有几个侧面 , 相邻侧面的公共边即侧棱都是平行的 . 它的棱也有两种 , 一种是侧棱 , 另一种就是底面上的边 . 激趣诱思 知识点拨 微思考 有两个面平行 , 其余各面都是平行四边形 , 这样的几何体一定是棱柱吗 ? 举例说明 . 提示 : 不一定 . 下图的几何体符合要求但不是棱柱 . 激趣诱思 知识点拨 微练习 下列命题正确的是 ( ) A. 四棱柱是平行六面体 B. 直平行六面体是长方体 C. 长方体的六个面都是矩形 D. 底面是矩形的四棱柱是长方体 解析 : 底面是平行四边形的四棱柱才是平行六面体 , 选项 A 错误 ; 底面是矩形的直平行六面体才是长方体 , 选项 B 错误 ; 底面是矩形的直四棱柱才是长方体 , 选项 D 错误 ; 选项 C 显然正确 . 答案 : C 激趣诱思 知识点拨 知识点三、棱锥的结构特征 1 . 棱锥的定义、分类、图形及表示 . 棱 锥 图形及表示 定义 一般地 , 有一个面是 多边形 , 其余各面都是 有一个公共顶点 的三角形 , 由这些面所围成的多面体叫做棱锥 用表示顶点和底面各顶点的字母表示 . 如图棱锥可记作 : 棱锥 S-ABCD 激趣诱思 知识点拨 棱 锥 图形及表示 相关 概念 底面 : 多边形 面叫做棱锥的底面 ; 侧面 : 有 公共顶点 的各个三角形面叫做棱锥的侧面 ; 侧棱 : 相邻侧面的 公共边 叫做棱锥的侧棱 ; 顶点 : 各侧面的公共顶点叫做棱锥的顶点 分类 ① 依据 : 底面多边形的边数 ; ② 举例 : 三棱锥 ( 底面是三角形 ) 、四棱锥 ( 底面是四边形 )…… 激趣诱思 知识点拨 2 . 正棱锥 : 底面是 正多边形 , 并且顶点与底面中心的连线 垂直 于底面的棱锥叫做正棱锥 . 微思考 有一个面是多边形 , 其余各面是三角形的多面体一定是棱锥吗 ? 提示 : 不一定 , 其余各面必须要有一个公共顶点 . 如图所示的几何体符合问题中的条件 , 但不是棱锥 . 激趣诱思 知识点拨 知识点四、棱台的结构特征 棱台的定义、分类、图形及表示 . 棱 台 图形及表示 定义 用一个 平行于 棱锥底面的平面去截棱锥 , 我们把底面和截面之间那部分多面体叫做棱台 用表示底面各顶点的字母表示 . 如图棱台可记作 : 棱台 ABCD-A'B'C'D ' 激趣诱思 知识点拨 棱 台 图形及表示 相关 概念 上底面 : 原棱锥的截面叫做棱台的上底面 ; 下底面 : 原棱锥的底面叫做棱台的下底面 ; 侧面 : 其余各面叫做棱台的侧面 ; 侧棱 : 相邻侧面的公共边叫做棱台的侧棱 ; 顶点 : 侧面与上 ( 下 ) 底面的公共顶点叫做棱台的顶点 分类 ① 依据 : 由几棱锥截得 ; ② 举例 : 三棱台 ( 由三棱锥截得 ) 、 四棱台 ( 由四棱锥截得 )…… 激趣诱思 知识点拨 名师点析 (1) 棱台上、下底面互相平行 , 且是两个相似的多边形 , 它们的面积之比等于截去的小棱锥的高与原棱锥的高的比的平方 . (2) 棱台的侧面均为梯形 . (3) 棱台各侧棱延长线交于一点 , 棱台问题可还原为棱锥问题解决 . 激趣诱思 知识点拨 微练习 (1) 下列几何体中 , 是棱柱 , 是棱锥 , 是棱台 ( 仅填相应序号 ) . 解析 : 结合棱柱、棱锥和棱台的定义可知 ①③④ 是棱柱 , ⑥ 是棱锥 , ⑤ 是棱台 . 答案 : ①③④ ⑥ ⑤ 激趣诱思 知识点拨 (2) 判断下列说法是否正确 , 正确的在后面的括号内画“ √ ” , 错误的画“ ×” . ① 有两个面互相平行 , 其余各面都是梯形的多面体是棱台 . ( ) ② 用一个平面去截棱锥 , 底面和截面之间的部分叫棱台 . ( ) ③ 棱台的各条侧棱延长后必交于一点 . ( ) 答案 : ① × ② × ③√ 探究一 探究二 素养形成 当堂检测 棱柱、棱锥、棱台的结构特征 角度 1 棱柱的结构特征 例 1 下列关于棱柱的说法 : ① 所有的面都是平行四边形 ; ② 每一个面都不会是三角形 ; ③ 两底面平行 , 并且各侧棱也平行 . 其中正确说法的序号是 . 解析 : ① 错误 , 底面可以是其他多边形而不光是平行四边形 ; ② 错误 , 底面可以是三角形 ; ③ 正确 , 由棱柱的定义可知 . 答案 : ③ 探究一 探究二 素养形成 当堂检测 反思感悟 关于棱柱的辨析 (1) 紧扣棱柱的结构特征进行有关概念辨析 . ① 两个面互相平行 ; ② 其余各面是四边形 ; ③ 相邻两个四边形的公共边互相平行 . (2) 多注意观察一些实物模型和图片便于反例排除 . 特别提醒 : 求解与棱柱相关的问题时 , 首先看是否有两个平行的面作为底面 , 再看是否满足其他特征 . 探究一 探究二 素养形成 当堂检测 变式训练 1 关于棱柱 , 下列说法正确的有 . ① 被平行于底面的平面截成的两部分可以都是棱柱 ; ② 棱柱的侧棱长相等 , 侧面都是平行四边形 ; ③ 各侧面都是正方形的四棱柱一定是正方体 . 解析 : ① 正确 , 被平行于底面的平面截成的两部分可以都是棱柱 ; ② 正确 , 由棱柱定义可知 , 棱柱的侧棱相互平行且相等 , 所以侧面均为平行四边形 ; ③ 不正确 , 上、下底面是菱形 , 各侧面是全等的正方形的四棱柱不一定是正方体 . 答案 : ①② 探究一 探究二 素养形成 当堂检测 角度 2 棱锥、棱台的结构特征 例 2 (1) 判断如图所示的物体是不是棱锥 , 为什么 ? (2) 如图所示的多面体是不是棱台 ? 探究一 探究二 素养形成 当堂检测 解 : (1) 该物体不是棱锥 . 因为棱锥的定义中要求 : 各侧面都是有一个公共顶点的三角形 , 但侧面 ABC 与侧面 CDE 没有公共顶点 , 所以该物体不是棱锥 . (2) 根据棱台的定义 , 可以得到判断一个多面体是棱台的标准有两个 : 一是共点 , 二是平行 . 即各侧棱延长线要交于一点 , 上、下底面要平行 , 二者缺一不可 . 据此 , 图 ① 中多面体侧棱延长线不相交于同一点 , 故不是棱台 ; 图 ② 中多面体侧棱延长线也不相交于同一点 , 不是棱台 ; 图 ③ 中多面体虽是由棱锥截得的 , 但截面与底面不平行 , 因此也不是棱台 . 探究一 探究二 素养形成 当堂检测 反思感悟 棱锥、棱台结构特征问题的判断方法 (1) 举反例法 结合棱锥、棱台的定义举反例直接说明关于棱锥、棱台结构特征的某些说法不正确 . (2) 直接法 棱锥 棱台 定底面 只有一个面是多边形 , 此面即为底面 两个互相平行的面 , 即为上、下底面 看侧棱 相交于一点 延长后相交于一点 探究一 探究二 素养形成 当堂检测 变式训练 2 有下列三个命题 : ① 用一个平面去截棱锥 , 棱锥底面和截面之间的部分是棱台 ; ② 两个面平行且相似 , 其余各面都是梯形的多面体是棱台 ; ③ 有两个面互相平行 , 其余四个面都是等腰梯形的六面体是棱台 . 其中正确的有 ( ) A.0 个 B.1 个 C.2 个 D.3 个 解析 : ① 中的平面不一定平行于底面 , 故 ① 错 ; ②③ 可用反例去检验 , 如图所示 , 侧棱延长线不能相交于一点 , 故 ②③ 错 . 故选 A . 答案 : A 探究一 探究二 素养形成 当堂检测 多面体表面距离最短问题 例 3 如图 , 在三棱锥 V-ABC 中 , VA=VB=VC= 4, ∠ AVB= ∠ AVC= ∠ BVC= 30°, 过点 A 作截面 △ AEF , 求 △ AEF 周长的最小值 . 分析 把三棱锥的侧面展开 , 当 △ AEF 的各边在同一直线上时 , 其周长最小 . 探究一 探究二 素养形成 当堂检测 解 : 将三棱锥沿侧棱 VA 剪开 , 并将其侧面展开平铺在一个平面上 , 如图 , 线段 AA 1 的长为所求 △ AEF 周长的最小值 . ∵∠ AVB= ∠ A 1 VC= ∠ BVC= 30 °, ∴∠ AVA 1 = 90° . 又 VA=VA 1 = 4, ∴ AA 1 = 4 , ∴△ AEF 周长的最小值为 4 . 反思感悟 本题是多面体表面上两点间的最短距离问题 , 常常要归结为求平面上两点间的最短距离问题 . 解决此类问题的方法就是先把多面体侧面展开 , 再用平面几何的知识来求解 . 探究一 探究二 素养形成 当堂检测 延伸探究 如图 , 在以 O 为顶点的三棱锥中 , 过点 O 的三条棱 , 任意两条棱的夹角都是 30°, 在一条棱上有 A , B 两点 , OA= 4, OB= 3, 以 A , B 为端点用一条绳子紧绕三棱锥的侧面一周 , 求此绳在 A , B 之间的最短绳长 . 解 : 作出三棱锥的侧面展开图 , 如图 .A , B 两点之间的最短绳长就是线段 AB 的长度 .OA= 4, OB= 3, ∠ AOB= 90°, 所以 AB= 5, 即此绳在 A , B 之间最短的绳长为 5 . 探究一 探究二 素养形成 当堂检测 几何体的平面展开图 典例 (1) 请画出如图所示的正方体的平面展开图 ; (2) 如图是两个几何体的平面展开图 , 请问各是什么几何体 ? 探究一 探究二 素养形成 当堂检测 解 : (1) 展开图如图所示 . ( 答案不唯一 ) 探究一 探究二 素养形成 当堂检测 (2) 根据平面展开图 , 可知 ① 为五棱柱 , ② 为三棱台 . 探究一 探究二 素养形成 当堂检测 方法点睛 (1) 绘制展开图 : 绘制多面体的平面展开图要结合多面体的几何特征 , 发挥空间想象能力或者是亲手制作多面体模型 . 在解题过程中 , 常常给多面体的顶点标上字母 , 先把多面体的底面画出来 , 然后依次画出各侧面 , 便可得到其平面展开图 . (2) 由展开图复原几何体 : 若是给出多面体的平面展开图 , 来判断是由哪一个多面体展开的 , 则可把上述过程逆推 . 同一个几何体的平面展开图可能是不一样的 , 也就是说 , 一个多面体可有多个平面展开图 . 探究一 探究二 素养形成 当堂检测 变式训练 如图所示 , 不是正四面体 ( 各棱长都相等的三棱锥 ) 的展开图的是 ( ) A. ①③ B. ②④ C . ③④ D. ①② 解析 : 可选择阴影三角形作为底面进行折叠 , 发现 ①② 可折成正四面体 , ③④ 折叠后只能围成无底的三棱锥 . 答案 : C 探究一 探究二 素养形成 当堂检测 1 . 有两个面平行的多面体不可能是 ( ) A. 棱柱 B. 棱锥 C. 棱台 D. 以上都不正确 解析 : 因为棱锥的任意两个面都相交 , 不可能有两个面平行 , 所以不可能是棱锥 . 答案 : B 2 . 棱台不具备的性质是 ( ) A. 两底面相似 B. 侧面都是梯形 C. 所有棱都相等 D. 侧棱延长后都交于一点 答案 : C 探究一 探究二 素养形成 当堂检测 3 . (2020 成都月考 ) 某人用如图所示的纸片 , 沿折痕折叠后粘成一个四棱锥形的 “ 走马灯 ”, 正方形做灯底 , 且有一个三角形面上写上了 “ 年 ” 字 , 当灯旋转时 , 正好看到 “ 新年快乐 ” 的字样 , 则在 ① 、 ② 、 ③ 处应依次写上 ( ) A. 快、新、乐 B . 乐、新、快 C. 新、乐、快 D . 乐、快、新 解析 : 根据四棱锥图形 , 正好看到 “ 新年快乐 ” 的字样 , 可知 ③ 处一定是 “ 乐 ” 字 , 故选 A . 答案 : A 探究一 探究二 素养形成 当堂检测 4 . 下列有关棱柱的说法 : ① 棱柱的所有的面都是平面 ; ② 棱柱的所有的棱长都相等 ; ③ 棱柱的所有的侧面都是长方形或正方形 ; ④ 棱柱的侧面的个数与底面的边数相等 ; ⑤ 棱柱的上、下底面全等 . 其中正确的有 . ( 填序号 ) 解析 : ② 棱柱的所有的侧棱棱长都相等 , 与底面的棱长不一定相等 , 故 ② 错误 ; ③ 棱柱的所有的侧面都是平行四边形 , 不一定都是长方形或正方形 , 故 ③ 错误 ; ①④⑤ 正确 . 答案 : ①④⑤ 探究一 探究二 素养形成 当堂检测 5 . 正方体 ABCD-A 1 B 1 C 1 D 1 的棱长为 2, 则在正方体表面上 , 从顶点 A 到顶点 C 1 的最短距离为 . 解析 : 将侧面 ABB 1 A 1 与底面 A 1 B 1 C 1 D 1 展开在同一平面上 , 连接 AC 1 , 则线段 AC 1 的长即为所求 . 如图 , AC 1 = 2 . 答案 : 2查看更多