- 2021-04-14 发布 |
- 37.5 KB |
- 8页
申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
中考复习专题动态几何之定值问题探讨
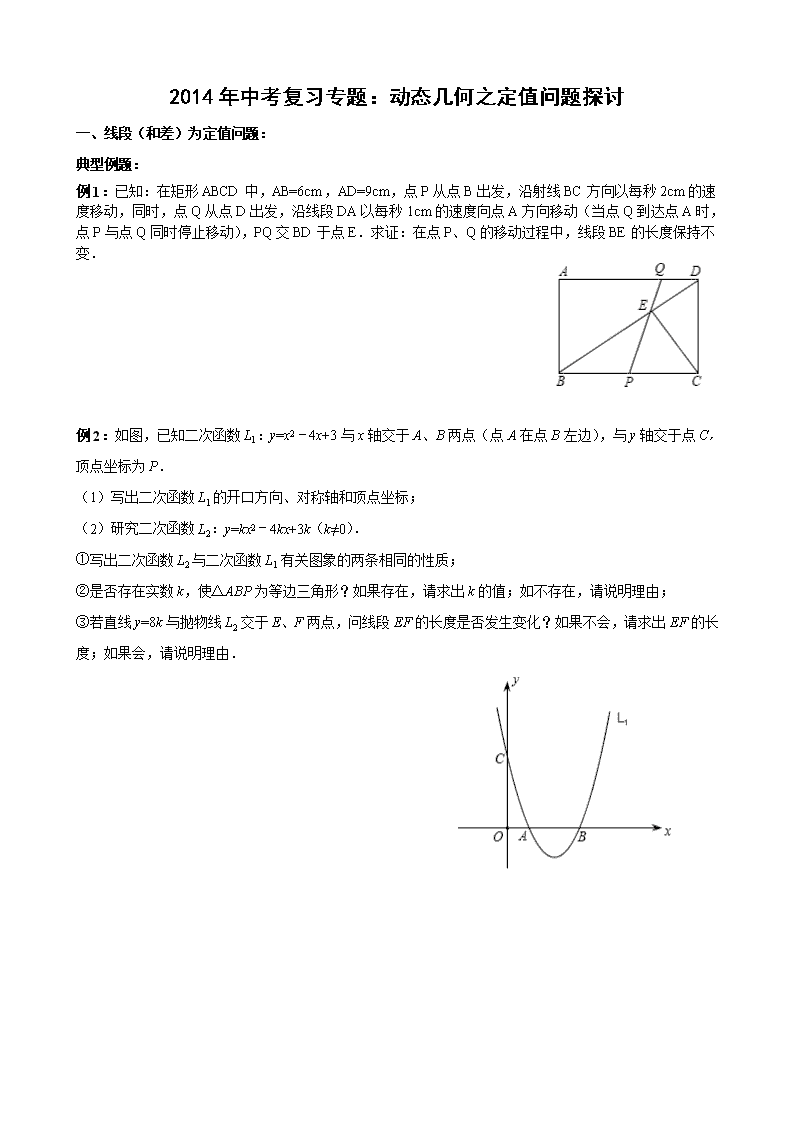
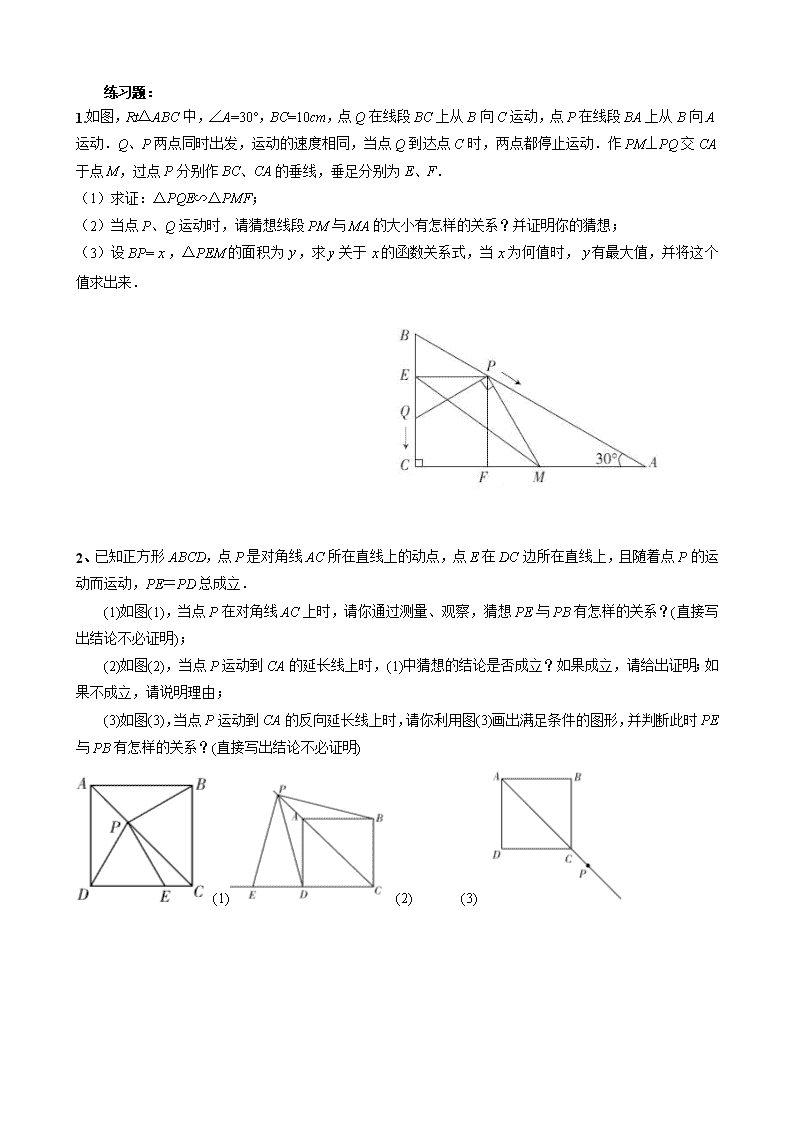
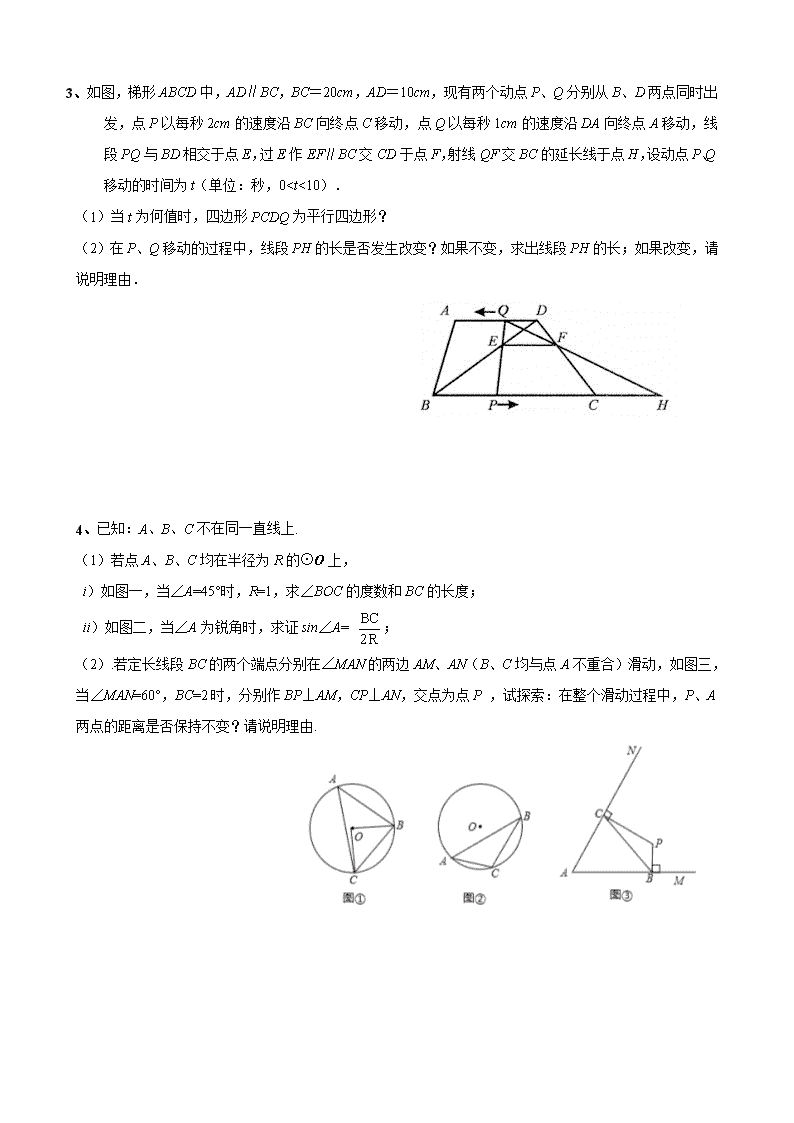
2014年中考复习专题:动态几何之定值问题探讨 一、线段(和差)为定值问题: 典型例题: 例1:已知:在矩形ABCD中,AB=6cm,AD=9cm,点P从点B出发,沿射线BC方向以每秒2cm的速度移动,同时,点Q从点D出发,沿线段DA以每秒1cm的速度向点A方向移动(当点Q到达点A时,点P与点Q同时停止移动),PQ交BD于点E.求证:在点P、Q的移动过程中,线段BE的长度保持不变. 例2:如图,已知二次函数L1:y=x2﹣4x+3与x轴交于A、B两点(点A在点B左边),与y轴交于点C,顶点坐标为P. (1)写出二次函数L1的开口方向、对称轴和顶点坐标; (2)研究二次函数L2:y=kx2﹣4kx+3k(k≠0). ①写出二次函数L2与二次函数L1有关图象的两条相同的性质; ②是否存在实数k,使△ABP为等边三角形?如果存在,请求出k的值;如不存在,请说明理由; ③若直线y=8k与抛物线L2交于E、F两点,问线段EF的长度是否发生变化?如果不会,请求出EF的长度;如果会,请说明理由. 练习题: 1.如图,Rt△ABC中,∠A=30°,BC=10cm,点Q在线段BC上从B向C运动,点P在线段BA上从B向A运动.Q、P两点同时出发,运动的速度相同,当点Q到达点C时,两点都停止运动.作PM⊥PQ交CA于点M,过点P分别作BC、CA的垂线,垂足分别为E、F. (1)求证:△PQE∽△PMF; (2)当点P、Q运动时,请猜想线段PM与MA的大小有怎样的关系?并证明你的猜想; (3)设BP=,△PEM的面积为,求y关于的函数关系式,当为何值时,有最大值,并将这个值求出来. 2、已知正方形ABCD,点P是对角线AC所在直线上的动点,点E在DC边所在直线上,且随着点P的运动而运动,PE=PD总成立. (1)如图(1),当点P在对角线AC上时,请你通过测量、观察,猜想PE与PB有怎样的关系?(直接写出结论不必证明); (2)如图(2),当点P运动到CA的延长线上时,(1)中猜想的结论是否成立?如果成立,请给出证明;如果不成立,请说明理由; (3)如图(3),当点P运动到CA的反向延长线上时,请你利用图(3)画出满足条件的图形,并判断此时PE与PB有怎样的关系?(直接写出结论不必证明) (1) (2) (3) 3、如图,梯形ABCD中,AD∥BC,BC=20cm,AD=10cm,现有两个动点P、Q分别从B、D两点同时出发,点P以每秒2cm的速度沿BC向终点C移动,点Q以每秒1cm的速度沿DA向终点A移动,线段PQ与BD相交于点E,过E作EF∥BC交CD于点F,射线QF交BC的延长线于点H,设动点P、Q移动的时间为t(单位:秒,0查看更多
相关文章
- 当前文档收益归属上传用户
- 下载本文档