- 2021-04-14 发布 |
- 37.5 KB |
- 18页
申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2008年数学中考试题分类汇编(反比例函数)
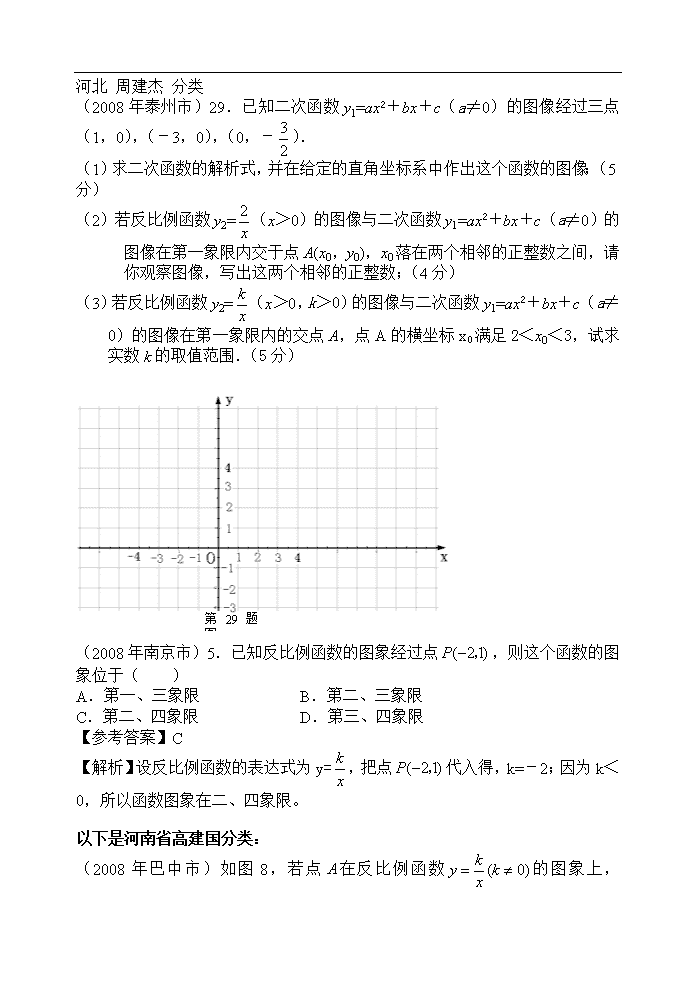
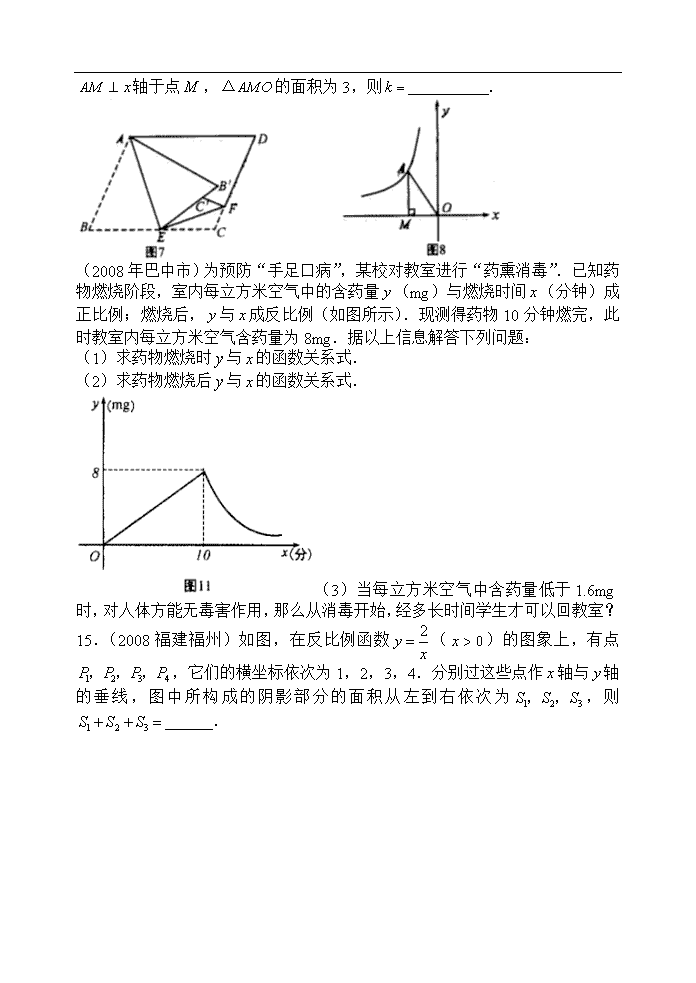
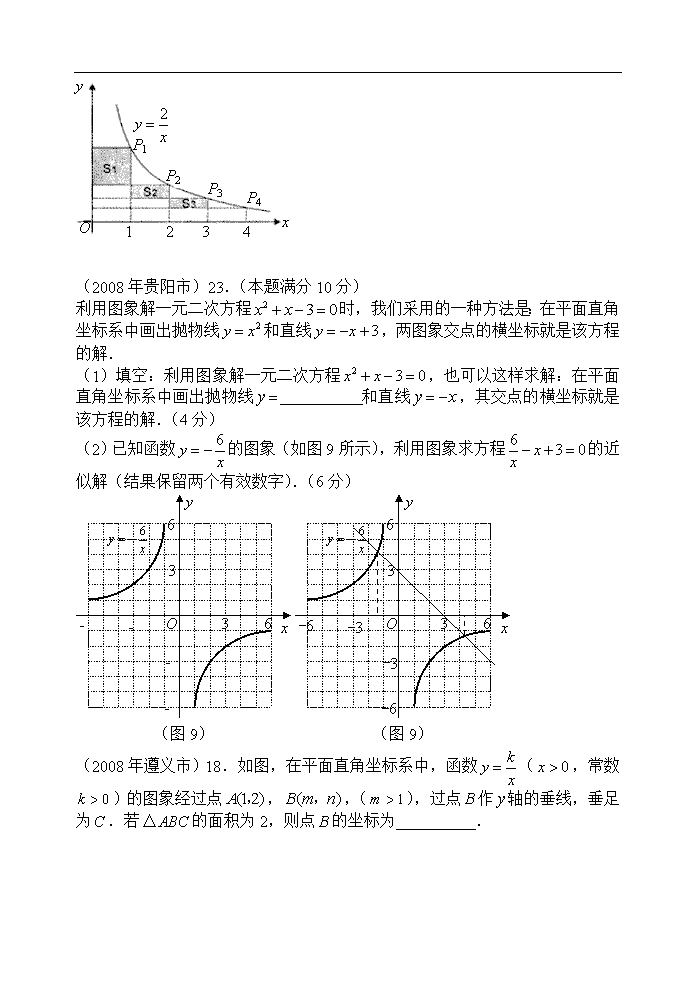
河北 周建杰 分类 (2008年泰州市)29.已知二次函数y1=ax2+bx+c(a≠0)的图像经过三点(1,0),(-3,0),(0,-). (1)求二次函数的解析式,并在给定的直角坐标系中作出这个函数的图像;(5分) (2)若反比例函数y2=(x>0)的图像与二次函数y1=ax2+bx+c(a≠0)的图像在第一象限内交于点A(x0,y0),x0落在两个相邻的正整数之间,请你观察图像,写出这两个相邻的正整数;(4分) (3)若反比例函数y2=(x>0,k>0)的图像与二次函数y1=ax2+bx+c(a≠0)的图像在第一象限内的交点A,点A的横坐标x0满足2<x0<3,试求实数k的取值范围.(5分) 第29题图 (2008年南京市)5.已知反比例函数的图象经过点,则这个函数的图象位于( ) A.第一、三象限 B.第二、三象限 C.第二、四象限 D.第三、四象限 【参考答案】C 【解析】设反比例函数的表达式为y=,把点代入得,k=-2;因为k<0,所以函数图象在二、四象限。 以下是河南省高建国分类: (2008年巴中市)如图8,若点在反比例函数的图象上, 轴于点,的面积为3,则 . (2008年巴中市)为预防“手足口病”,某校对教室进行“药熏消毒”.已知药物燃烧阶段,室内每立方米空气中的含药量(mg)与燃烧时间(分钟)成正比例;燃烧后,与成反比例(如图所示).现测得药物10分钟燃完,此时教室内每立方米空气含药量为8mg.据以上信息解答下列问题: (1)求药物燃烧时与的函数关系式. (2)求药物燃烧后与的函数关系式. (3)当每立方米空气中含药量低于1.6mg时,对人体方能无毒害作用,那么从消毒开始,经多长时间学生才可以回教室? 15.(2008福建福州)如图,在反比例函数()的图象上,有点,它们的横坐标依次为1,2,3,4.分别过这些点作轴与轴的垂线,图中所构成的阴影部分的面积从左到右依次为,则 . x y O P1 P2 P3 P4 1 2 3 4 (2008年贵阳市)23.(本题满分10分) 利用图象解一元二次方程时,我们采用的一种方法是:在平面直角坐标系中画出抛物线和直线,两图象交点的横坐标就是该方程的解. (1)填空:利用图象解一元二次方程,也可以这样求解:在平面直角坐标系中画出抛物线 和直线,其交点的横坐标就是该方程的解.(4分) (2)已知函数的图象(如图9所示),利用图象求方程的近似解(结果保留两个有效数字).(6分) (图9) y x O 3 6 6 3 -3 -6 -6 -3 (图9) y x O 3 6 6 3 -3 -6 -6 -3 (2008年遵义市)18.如图,在平面直角坐标系中,函数(,常数)的图象经过点,,(),过点作轴的垂线,垂足为.若的面积为2,则点的坐标为 . y O (18题图) x C A(1,2) B(m,n) 1. (2008年郴州市)已知一次函数y=ax+b的图像与反比例函数 的图像交于A(2,2),B(-1,m),求一次函数的解析式. 辽宁省 岳伟 分类 2008年郴州市 已知一次函数y=ax+b的图像与反比例函数 的图像交于A(2,2),B(-1,m),求一次函数的解析式. 22. ( 2008年杭州市) (第22题) 为了预防流感,某学校在休息天用药熏消毒法对教室进行消毒.已知药物释放过程中,室内每立方米空气中的含药量(毫克)与时间(小时)成正比;药物释放完毕后,与的函数关系式为(为常数),如图所示.据图中提供的信息,解答下列问题: (1) 写出从药物释放开始,与之间的两个函数关系式及相应的自变量的取值范围; (2)据测定,当空气中每立方米的含药量降低到毫克以下时,学生方可进入教室,那么从药物释放开始,至少需要经过多少小时后,学生才能进入教室? 2.(2008年•南宁市)图5是反比例函数的图象,那么实数的取值范围是 7.(2008年双柏县)已知甲、乙两地相距(km),汽车从甲地匀速行驶到乙地,则汽车行驶的时间(h)与行驶速度(km/h)的函数关系图象大致是( ) t/h v/(km/h) O t/h v/(km/h) O t/h v/(km/h) O t/h v/(km/h) O A. B. C. D. (08年宁夏回族自治区) 反比例函数(k>0)的部分图象如图所示,A、B是图象上两点,AC⊥轴于点C,BD⊥轴于点D,若△AOC的面积为S,△BOD的面积为S,则S和S 的大小关系为( ) A.S> S B。S= S C。S <S D。无法确定 以下是辽宁省高希斌的分类 1.(2008年湖北省咸宁市)两个反比例函数和在第一象限内的图象如图所示,点P在的图象上,PC⊥x轴于点C,交的图象于点A,PD⊥y轴于点D,交的图象于点B,当点P在的图象上运动时,以下结论: ①△ODB与△OCA的面积相等; ②四边形PAOB的面积不会发生变化;③PA与PB始终相等; ④当点A是PC的中点时,点B一定是PD的中点. 其中一定正确的是 (把你认为正确结论的序号都填上,少填或错填不给分). x y O A P C Q B (第12题图) 2.(2008年荆州市)如图,一次函数的图象分别交x轴、y轴于A、B,P为AB上一点且PC为△AOB的中位线,PC的延长线交反比例函数的图象于Q,,则k的值和Q点的坐标分别为_________________________. 3.(2008年湖北省鞥仙桃市潜江市江汉油田)对于反比例函数(),下列说法不正确的是 A. 它的图象分布在第一、三象限 B. 点(,)在它的图象上 C. 它的图象是中心对称图形 D. 随的增大而增大 .(2008年龙岩市)若的图象分别位于第一、第三象限,则k的取值范围是 . 2(2008乌鲁木齐).反比例函数的图象位于( )答案B A.第一、三象限 B.第二、四象限 C.第二、三象限 D.第一、二象限 12(云南省2008年).函数中 ,自变量的取值范围是_________.答案: 22(云南省2008年).(本小题8分)已知,在同一直角坐标系中,反比例函数与二次函数的图像交于点. (1)求、的值; (2)求二次函数图像的对称轴和顶点坐标. (梅州)已知直线与双曲线的一个交点A的坐标为(-1,-2).则=_____;=____;它们的另一个交点坐标是______. (茂名)已知反比例函数=(≠0)的图象,在每一象限内,的值随值的增大而减少,则一次函数=-+的图象不经过( )C A.第一象限 B.第二象限 C.第三象限 D.第四象限 以下是江苏省赣榆县罗阳中学李金光分类: 1.(2008年南昌市)下列四个点,在反比例函数图象上的是( ) A.(1,) B.(2,4) C.(3,) D.(,) 2.(2008年沈阳市)下列各点中,在反比例函数图象上的是( ) A. B. C. D. 3.(2008年大连市)函数的图象经过点(1,2),则k的值为____________. 13.(2008年义乌市)函数,当时没有意义,则的值为 ▲ . 22.(2008年义乌市)已知:等腰三角形OAB在直角坐标系中的位置如图,点A的坐标为(),点B的坐标为(-6,0). (1)若三角形OAB关于y轴的轴对称图形是三角形O, 请直接写出A、B的对称点的坐标; (2)若将三角形沿x轴向右平移a个单位,此时点A 恰好落在反比例函数的图像上,求a的值; (3)若三角形绕点O按逆时针方向旋转度(). ①当=时点B恰好落在反比例函数的图像上,求k的值. ②问点A、B能否同时落在①中的反比例函数的图像上,若能,求出 的值;若不能,请说明理由. x y C O A B (第6题) 6.(2008年宁波市)如图,正方形的边长为2,反比例函数过点,则的值是( ) A. B. C. D. 6.(2008嘉兴市)某反比例函数的图象经过点,则此函数图象也经过点( ) A. B. C. D. (2008年芜湖市)在平面直角坐标系中,直线向上平移1个单位长度得到直线.直线与反比例函数的图象的一个交点为,则的值等于 . (2008年安徽省)函数的图象经过点(1,-2),则k的值为…………【 】 A. B. C.2 D.-2 13.(2008年芜湖市)在平面直角坐标系中,直线向上平移1个单位长度得到直线.直线与反比例函数的图象的一个交点为,则的值等于 . 答案:2 解析:本题主要考察一次函数和反比例函数的表达式。本题中由直线向上平移1个单位长度得到直线的表达式y=x+1,将A点坐标代入求出a=1,再将A的坐标(1,2)代入反比例函数的表达式得出k=2。一次函数图像向上平移时y=kx+b中b的值增加。通过一次函数的表达式求出a再去求k的值。 13.(2008年义乌市)函数,当时没有意义,则的值为 ▲ . 22.(2008年义乌市)已知:等腰三角形OAB在直角坐标系中的位置如图,点A的坐标为(),点B的坐标为(-6,0). (1)若三角形OAB关于y轴的轴对称图形是三角形O, 请直接写出A、B的对称点的坐标; (2)若将三角形沿x轴向右平移a个单位,此时点A 恰好落在反比例函数的图像上,求a的值; (3)若三角形绕点O按逆时针方向旋转度(). ①当=时点B恰好落在反比例函数的图像上,求k的值. ②问点A、B能否同时落在①中的反比例函数的图像上,若能,求出 的值;若不能,请说明理由. x y C O A B (第6题) 6.(2008年宁波市)如图,正方形的边长为2,反比例函数过点,则的值是( ) A. B. C. D. 6.(2008嘉兴市)某反比例函数的图象经过点,则此函数图象也经过点( ) A. B. C. D. 以下是江苏董耀波的分类 (2008黄冈市)已知反比例函数y=,下列结论中,不正确的是( ) A.图象必经过点(1,2) B.y随x的增大而减少 C.图象在第一、三象限内 D.若x>1,则y<2 (2008襄樊市)在一个可以改变体积的密闭容器内装有一定质量的二氧化碳,当改变容器的体积时,气体的密度也会随之改变,密度(单位:kg/m3)是体积(单位:m3)的反比例函数,它的图象如图3所示,当时,气体的密度是( ) A.5kg/m3 B.2kg/m3 C.100kg/m3 D,1kg/m3 (2008恩施自治州)如图5,一次函数y=x-1与反比例函数y=的图像交于点A(2,1),B(-1,-2),则使y>y的x的取值范围是 A. x>2 B. x>2 或-1<x<0 C. -1<x<2 D. x>2 或x<-1 O B y x AAA 图5 (2008黄冈市)已知反比例函数y=,下列结论中,不正确的是( ) A.图象必经过点(1,2) B.y随x的增大而减少 (2008襄樊市)在一个可以改变体积的密闭容器内装有一定质量的二氧化碳,当改变容器的体积时,气体的密度也会随之改变,密度(单位:kg/m3)是体积(单位:m3)的反比例函数,它的图象如图3所示,当时,气体的密度是( ) A.5kg/m3 B.2kg/m3 C.100kg/m3 D,1kg/m3 (2008恩施自治州)如图5,一次函数y=x-1与反比例函数y=的图像交于点A(2,1),B(-1,-2),则使y>y的x的取值范围是 A. x>2 B. x>2 或-1<x<0 C. -1<x<2 D. x>2 或x<-1 O B y x AAA 图5 (2008常州市) 若反比例函数的图象在其每个象限内,y随x的增大而减小,则k的值可以是 A.-1 B.3 C.0 D.-3 (2008常州市) _ 4 6过反比例函数的图象上的一点分别作x、y轴的垂线段,如果垂线段与x、y轴所围成的矩形面积是6,那么该函数的表达式是______;若点A(-3,m)在这个反比例函数的图象上,则m=______. (2008苏州)如图,帆船和帆船在太湖湖面上训练,为湖面上的一个定点,教练船静候于点.训练时要求两船始终关于点对称.以为原点,建立如图所示的坐标系,轴,轴的正方向分别表示正东、正北方向.设两船可近似看成在双曲线上运动.湖面风平浪静,双帆远影优美.训练中当教练船与两船恰好在直线上时,三船同时发现湖面上有一遇险的船,此时教练船测得船在东南方向上,船测得与的夹角为,船也同时测得船的位置(假设船位置不再改变,三船可分别用三点表示). (1)发现船时,三船所在位置的坐标分别为和; (2)发现船,三船立即停止训练,并分别从三点出发船沿最短路线同时前往救援,设两船的速度相等,教练船与船的速度之比为,问教练船是否最先赶到?请说明理由. y x A B O 1 1 C (百米) (百米) (第25题) (威海市)如图,点A(m,m+1),B(m+3,m-1)都在反比例函数的图象上. x O y A B (1)求m,k的值; (2)如果M为x轴上一点,N为y轴上一点, 以点A,B,M,N为顶点的四边形是平行四边形, 友情提示:本大题第(1)小题4分,第(2)小题7分.对完成第(2)小题有困难的同学可以做下面的(3)选做题.选做题2分,所得分数计入总分.但第(2)、(3)小题都做的,第(3)小题的得分不重复计入总分. 试求直线MN的函数表达式. (2008年广东湛江市)11. 已知三角形的面积一定,则它底边上的高与底边之间的函数关系的图象大致是( )D h a O h a O h a O h a O A. B. C. D . (2008年西宁市) 19.如图8,已知函数中,时,随的增大而增大,则的大致图象为( )A A. x y O B. x y O C. x y O D. x y O 图8 (2008年西宁市) 6.如图3所示的是函数与的图象,求方程组的解关于原点对称的点的坐标是 ;在平面直角坐标系中,将点向左平移6个单位,再向下平移1个单位,恰好在函数的图象上,则此函数的图象分布在第 象限.,二、四 图3 x y O 3 4 二、填空题 1.(2008年甘肃省白银市)一个函数具有下列性质: ①它的图像经过点(-1,1);②它的图像在二、四象限内; ③在每个象限内,函数值y随自变量x的增大而增大.则这个函数的解析式可以为 . 以下是山西省王旭亮分类 (2008年重庆市)已知:如图,反比例函数的图象经过点A、B,点A的坐标为(1,3),点B的纵坐标为1,点C的坐标为(2,0). (1)求该反比例函数的解析式; (2)求直线BC的解析式. (2008年上海市)在平面直角坐标系中,如果双曲线经过点,那么 . 以下是江苏省王伟根分类 2008年全国中考数学试题分类汇编(反比例函数) 1.(2008年扬州市)函数的图象与直线没有交点,那么k的取值范围是 A、 B、 C、 D、 2.(2008年江西省)若点(x0,y0)在函数y=( x<0)的图象上,且x0y0=-2,则它的图象大致是 ( ) y x O y O x y O x y O x A. B. C. D. 3. (2008盐城)阅读理解:对于任意正实数a、b,∵≥0, ∴≥0, ∴≥,只有当a=b时,等号成立. 结论:在≥(a、b均为正实数)中,若ab为定值p,则a+b≥ ,只有当a=b时,a+b有最小值. 根据上述内容,回答下列问题: D C B A O 第26题图1 若m>0,只有当m= ▲ 时, ▲ . 思考验证:如图1,AB为半圆O的直径,C为半圆上任意一点(与点A、B不重合),过点C作CD⊥AB,垂足为D,AD=a,DB=b.试根据图形验证≥,并指出等号成立时的条件. 第26题图2 探索应用:如图2,已知A(-3,0),B(0,-4),P为双曲线(x>0)上的任意一点,过点P作PC⊥x轴于点C,PD⊥y轴于点D.求四边形ABCD面积的最小值,并说明此时四边形ABCD的形状. 以下是湖南文得奇的分类: 1.(2008年湘潭) .已知双曲线经过点(2,5),则k= . 2.(2008年益阳) 物理学知识告诉我们,一个物体所受到的压强P与所受压力F及受力面积S之间的计算公式为. 当一个物体所受压力为定值时,那么该物体所受压强P与受力面积S之间的关系用图象表示大致为 O P S S O P O P S O P A B C D S 3.(2008年永州) (10分)如图,已知⊙O的直径AB=2,直线m与⊙O相切于点A,P为⊙O上一动点(与点A、点B不重合),PO的延长线与⊙O相交于点C,过点C的切线与直线m相交于点D. (1)求证:△APC∽△COD. (2)设AP=x,OD=y,试用含x的代数式表示y. (3)试探索x为何值时,△ACD是一个等边三角形. (以下是安徽张仕春分类) 1.(2008年内江市) 若,两点均在函数的图象上,且,则与的大小关系为( ) A. B. C. D.无法判断 2.(2008年内江市) 如图,一次函数的图象经过第一、二、三象限,且与反比例函数图象相交于两点,与轴交于点,与轴交于点,.且点横坐标是点纵坐标的2倍. (1)求反比例函数的解析式; (2)设点横坐标为,面积为, 求与的函数关系式,并求出自变量的取值范围. 2(2008乌鲁木齐).反比例函数的图象位于( )答案B A.第一、三象限 B.第二、四象限 C.第二、三象限 D.第一、二象限 (08河南) 11.已知反比例函数的图象经过点(m,2)和(-2,3)则m的值为 . 15、(08河南试验区)如图,直线(>0)与双曲线在第一象限内的交点面积为R,与轴的交点为P,与轴的交点为Q;作RM⊥轴于点M,若△OPQ与△PRM的面积是4:1,则 15. ((2008年湖北省宜昌市)某物体对地面的压力为定值,物体对地面的压强p(Pa)与受力面积S(㎡)之间的函数关系如图所示.这一函数表达式为p=________. 15.(2008年武汉市)如图,半径为5的⊙P与轴交于点M(0,-4),N(0,-10),函数的图像过点P,则= . 以下是安徽省马鞍山市成功中学的汪宗兴老师的分类 7.(2008年·东莞市)经过点A(1,2)的反比例函数解析式是_____ _____; 1、(2008年宜宾市)若正方形AOBC的边OA、OB在坐标轴上,顶点C在第一象限且在反比例函数y=的图像上,则点C的坐标是 答 2008年广州市数学中考试题)21、(12分)如图8,一次函数的图象与反比例函数的图象相交于A、B两点 (1)根据图象,分别写出A、B的坐标; (2)求出两函数解析式; (3)根据图象回答:当为何值时, 一次函数的函数值大于反比例函数的函数值 y x O (第9题) 1.(2008年泰安市)函数的图象如图所示,下列对该函数性质的论断不可能正确的是( ) A.该函数的图象是中心对称图形 B.当时,该函数在时取得最小值2 C.在每个象限内,的值随值的增大而减小 D.的值不可能为1 2.(2008年聊城市)已知一次函数与反比例函数的图象交于点. (1)求这两个函数的函数关系式; (2)在给定的直角坐标系(如图)中,画出这两个函数的大致图象; O 1 2 3 4 5 6 6 5 4 3 2 1 -1 -2 -3 -4 -5 -6 -1 -2 -3 -4 -5 -6 x y 第23题图 (3)当为何值时,一次函数的值大于反比例函数的值?当为何值时,一次函数的值小于反比例函数的值? 1、(2008年宜宾市)若正方形AOBC的边OA、OB在坐标轴上,顶点C在第一象限且在反比例函数y=的图像上,则点C的坐标是 2.(四川省资阳市)若A(,)、B(,)在函数的图象上,则当、满足_______________时, 3.(四川省资阳市)若一次函数y=2x-1和反比例函数y=的图象都经过点(1,1). (1)求反比例函数的解析式; (2)已知点A在第三象限,且同时在两个函数的图象上,求点A的坐标; (3)利用(2)的结果,若点B的坐标为(2,0),且以点A、O、B、P为顶点的四边形是平行四边形,请你直接写出点P的坐标.·查看更多