【推荐】专题24+平面向量的数量积与平面向量应用举例-2019年高三数学（理）二轮必刷题

【推荐】专题24+平面向量的数量积与平面向量应用举例-2019年高三数学（理）二轮必刷题

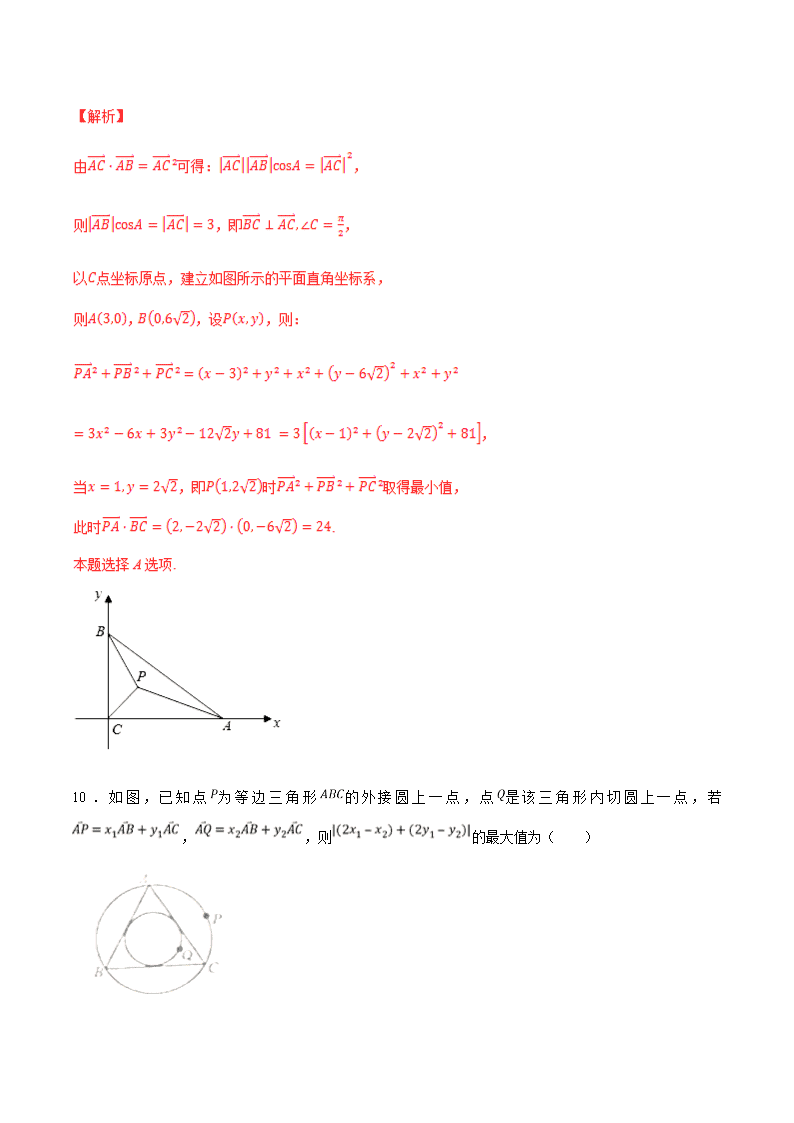
专题24 平面向量的数量积与平面向量应用举例 ‎1．已知向量的夹角为，且，则( )‎ A． B．2 C． D．84‎ ‎【答案】C ‎2．如图，圆是边长为4的正方形的内切圆，是圆的内接正三角形，若绕着圆心旋转，则的最大值是（ ）‎ A． B．‎ C． D．‎ ‎【答案】D ‎【解析】‎ 由题意，可得，‎ 又由，‎ 所以，‎ 又因为,‎ 所以，‎ 所以的最大值为，故选D. ‎ ‎8．设分别是的内角的对边，已知，设是边的中点，且的面积为，则等于（ ）‎ A．2 B．4 C．-4 D． -2‎ ‎【答案】A ‎9．在中，，，点是所在平面内一点，则当取得最小值时，（ ）‎ A．24 B． C． D．‎ ‎【答案】A ‎10．如图，已知点为等边三角形的外接圆上一点，点是该三角形内切圆上一点，若，，则的最大值为（ ）‎ A． B．2 C． D．‎ ‎【答案】C ‎11．已知动点P是边长为的正方形ABCD的边上任意一点，MN是正方形ABCD的外接圆O的一条动弦，且MN=，则的取值范围是___________.‎ ‎【答案】‎ ‎12．如图，梯形ABCD中，，，，，E是BC上一动点，则的最小值为______‎ ‎【答案】‎ 当时，有最小值，‎ 故答案为：. ‎ ‎19．已知抛物线的焦点为，的三个顶点都在抛物线上，且.‎ ‎（1）证明:两点的纵坐标之积为定值；‎ ‎（2）设，求的取值范围.‎ ‎【答案】（1）见解析；（2）.‎ 故的 ‎20．在中， ， ， ，若， ，且．‎ ‎（）求向量在向量方向上的投影．‎ ‎（）求实数的值．‎ ‎【答案】（）；（）．‎ ‎【解析】‎ ‎（），‎