- 2021-04-13 发布 |
- 37.5 KB |
- 6页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2016届高考数学(理)大一轮复习达标训练试题:板块命题点专练(十) 推理与证明
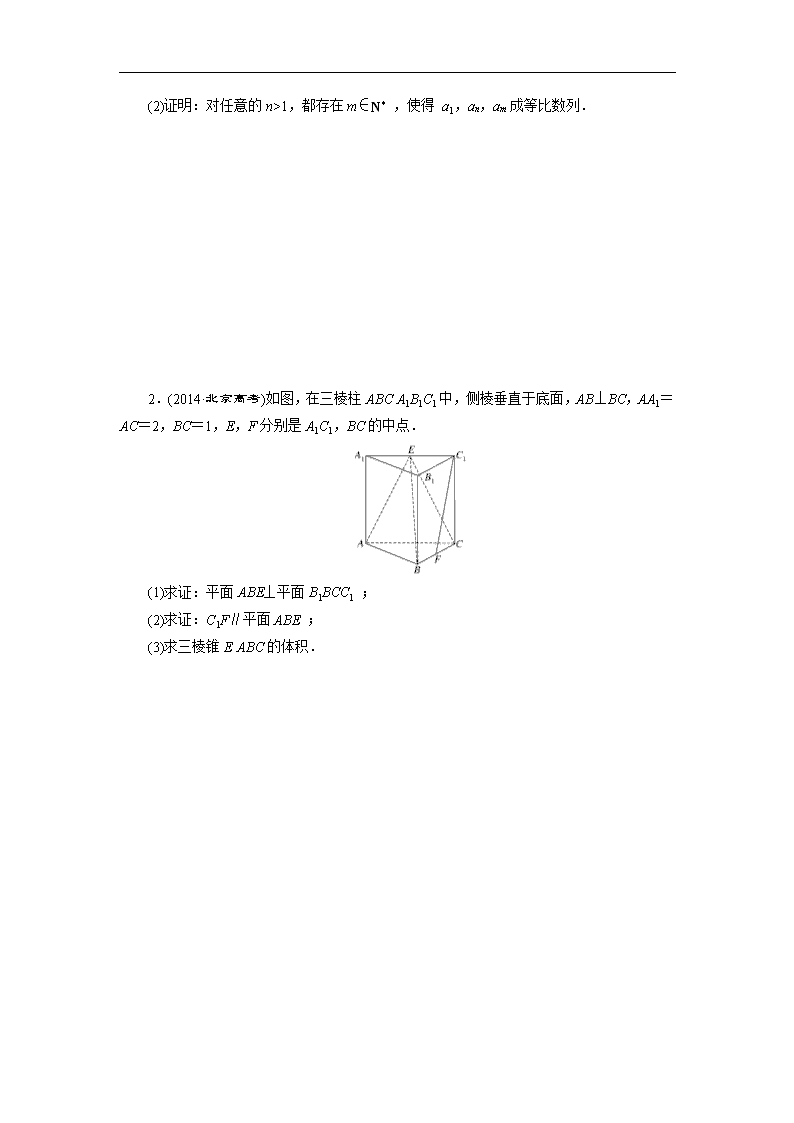
板块命题点专练(十) 推理与证明 (研近年高考真题——找知识联系,找命题规律,找自身差距) 命题点一 合情推理与演绎推理 命题指数:☆☆☆ 难度:中、低 题型:选择题、填空题 1.(2014·陕西高考)观察分析下表中的数据: 多面体 面数(F) 顶点数(V) 棱数(E) 三棱柱 5 6 9 五棱锥 6 6 10 立方体 6 8 12 猜想一般凸多面体中F,V,E所满足的等式是____________. 2.(2014·新课标全国卷Ⅰ)甲、乙、丙三位同学被问到是否去过A,B,C三个城市时, 甲说:我去过的城市比乙多,但没去过B城市; 乙说:我没去过C城市; 丙说:我们三人去过同一个城市. 由此可判断乙去过的城市为________. 3.(2013·湖北高考)古希腊毕达哥拉斯学派的数学家研究过各种多边形数.如三角形数1,3,6,10,…,第n个三角形数为=n2+n.记第n个k边形数为N(n,k)(k≥3),以下列出了部分k边形数中第n个数的表达式: 三角形数 N(n,3)=n2+n, 正方形数 N(n,4)=n2, 五边形数 N(n,5)=n2-n, 六边形数 N(n,6)=2n2-n, …… 可以推测N(n,k)的表达式,由此计算N(10,24)=________. 命题点二 直接证明与间接证明 命题指数:☆☆☆☆☆ 命题指数:☆☆☆☆☆ 难度:高、中题型:解答题 1.(2014·江西高考)已知数列{an} 的前 n项和 Sn=,n∈N*. (1)求数列{an} 的通项公式; (2)证明:对任意的n>1,都存在m∈N* ,使得 a1,an,am成等比数列. 2.(2014·北京高考)如图,在三棱柱ABCA1B1C1中,侧棱垂直于底面,AB⊥BC,AA1=AC=2,BC=1,E,F分别是A1C1,BC的中点. (1)求证:平面ABE⊥平面B1BCC1 ; (2)求证:C1F∥平面ABE ; (3)求三棱锥EABC的体积. 命题点三 数学归纳法 命题指数:☆☆ 难度:高 题型:解答题 (2014·江苏高考)已知函数f0(x)=(x>0),设fn(x)为fn-1(x)的导数,n∈N*. (1)求2f1+f2的值; (2)证明:对任意的n∈N*,等式nfn-1+fn=都成立. 答案 命题点一 1.解析:三棱柱中5+6-9=2;五棱锥中6+6-10=2;立方体中6+8-12=2,由此归纳可得F+V-E=2. 答案:F+V-E=2 2.解析:由甲、丙的回答易知甲去过A城市和C城市,乙去过A城市或C城市,结合乙的回答可得乙去过A城市. 答案:A 3.解析:由N(n,3)=n2+n, N(n,4)=n2+n, N(n,5)=+n, N(n,6)=n2+n, 推测N(n,k)=n2-n,k≥3.从而N(n,24)=11n2-10n,N(10,24)=1 000. 答案:1 000 命题点二 1.解:(1)由Sn=,得a1=S1=1, 当n≥2时,an=Sn-Sn-1=3n-2,当n=1时也适合. 所以数列{an}的通项公式为:an=3n-2. (2)证明:要使得a1,an,am成等比数列, 只需要a=a1·am, 即(3n-2)2=1·(3m-2), 即m=3n2-4n+2,而此时m∈N*,且m>n. 所以对任意的n>1,都存在m∈N*,使得a1,an,am成等比数列. 2.解:(1)证明:在三棱柱ABCA1B1C1中,BB1⊥底面ABC. 所以BB1⊥AB. 又因为AB⊥BC,BB1∩BC=B, 所以AB⊥平面B1BCC1. 又AB⊂平面ABE. 所以平面ABE⊥平面B1BCC1. (2)证明:取AB中点G,连结EG,FG. 因为E,F分别是A1C1,BC的中点, 所以FG∥AC,且FG=AC. 因为AC∥A1C1,且AC=A1C1, 所以FG∥EC1,且FG=EC1. 所以四边形FGEC1为平行四边形. 所以C1F∥EG. 又因为EG⊂平面ABE,C1F⊄平面ABE, 所以C1F∥平面ABE. (3)因为AA1=AC=2,BC=1,AB⊥BC, 所以AB==. 所以三棱锥EABC的体积 V=S△ABC·AA1=×××1×2=. 命题点三 解:(1)由已知, 得f1(x)=f′0(x)=′=-, 于是f2(x)=f′1(x)=′-′=--+, 所以f1=-,f2=-+. 故2f1+f2=-1. (2)证明:由已知,得xf0(x)=sin x,等式两边分别对x求导,得f0(x)+xf′0(x)=cos x, 即f0(x)+xf1(x)=cos x=sin, 类似可得 2f1(x)+xf2(x)=-sin x=sin(x+π), 3f2(x)+xf3(x)=-cos x=sin, 4f3(x)+xf4(x)=sin x=sin(x+2π). 下面用数学归纳法证明等式nfn-1(x)+xfn(x)=sin对所有的n∈N*都成立. ①当n=1时,由上可知等式成立. ②假设当n=k时等式成立, 即kfk-1(x)+xfk(x)=sin. 因为[kfk-1(x)+xfk(x)]′=kf′k-1(x)+fk(x)+xf′k(x) =(k+1)fk(x)+xfk+1(x), ′=cos·′=sin, 所以(k+1)fk(x)+xfk+1(x)=sin. 因此当n=k+1时,等式也成立. 综合①②可知等式nfn-1(x)+xfn(x)=sin对所有的n∈N*都成立. 令x=, 可得nfn-1+fn=sin(n∈N*). 所以=(n∈N*).查看更多