- 2021-04-13 发布 |
- 37.5 KB |
- 16页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
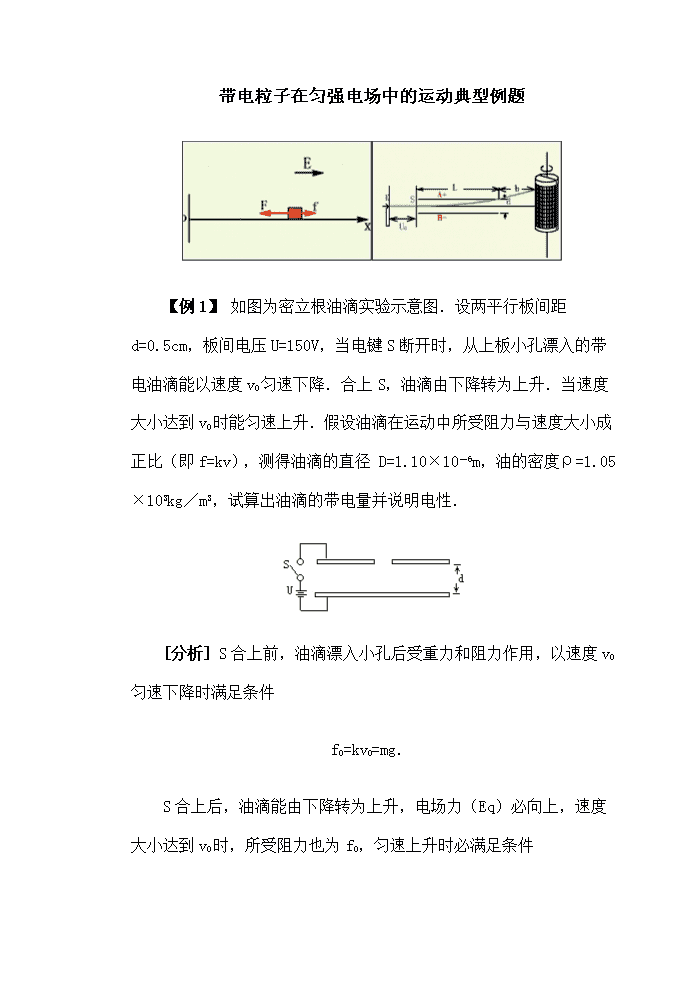
带电粒子在匀强电场中的运动典型例题
带电粒子在匀强电场中的运动典型例题 【例1】 如图为密立根油滴实验示意图.设两平行板间距d=0.5cm,板间电压U=150V,当电键S断开时,从上板小孔漂入的带电油滴能以速度v0匀速下降.合上S,油滴由下降转为上升.当速度大小达到v0时能匀速上升.假设油滴在运动中所受阻力与速度大小成正比(即f=kv),测得油滴的直径 D=1.10×10-6m,油的密度ρ=1.05×103kg/m3,试算出油滴的带电量并说明电性. [分析] S合上前,油滴漂入小孔后受重力和阻力作用,以速度v0匀速下降时满足条件 f0=kv0=mg. S合上后,油滴能由下降转为上升,电场力(Eq)必向上,速度大小达到v0时,所受阻力也为f0,匀速上升时必满足条件 Eq=mg+f0=2mg. 式中 因油滴所受电场力方向与板间场强方向相反,故油滴带负电. [说明] 密立根在实验中测定了许多油滴的带电量,发现它们都是某个基本单位的整数倍,从而证实了自然界中存在着一个最小电量的电荷,称为基元电荷,e=1.6×10-19C.因此,必须明白,密立根并没有直接测出单个电子的电量,而是根据对油滴带电量的综合分析推理得出的. 【例2】 图1中A、B是一对平行的金属板.在两板间加上一周期为T的交变电压u.A板的电势UA=0,B板的电势UB随时间的变化规律为:在 0到 T/2的时间内,UB=U0(正的常数);在T/2到T的时间内,UB=-U0;在T到3T/2的时间内,UB=U0;在3T/2到2T的时间内,UB=-U0…现有一电子从A板上的小孔进入两板间的电场区内,设电子的初速度和重力影响均可忽略, A.若电子是在t=0时刻进入的.它将一直向B板运动 B.若电子是在 t=T/8时刻进入的,它可能时而向 B板运动,时而向A板运动,最后打在B板上 C.若电子是在t=3T/8时刻进入的,它可能时而向B板运动,时而向A板运动,最后打在B板上 D.若电子是在t=T/2时刻进入的,它可能时而向 B板、时而向A板运动 [分析] B板电势的变化规律如图2所示.A、B两板间的电场强度大小恒定,方向周期性变化.电子所受的电场力也是大小恒定,方向周期性变化,即 着B板作匀减速运动,直至速度减为零.然后,电子又加速、减速,……如此一直向着B板运动.其v-t图如图所示,A正确. 向着B板作匀 减速运动,直到速度减为零,然后在余下的 零,然后又重复着第一次进入时的运动.由于t轴上方图线所围面积大于下方面积,即电子向B板的位移大于向A板的位移,电子最后能抵达B板.其v-t图如图④所示,B正确. 电子先向B板作匀加速运动,后作匀减速运动,速度减至零后,接着向A板作匀加速运动,其v-t 图如图⑤所示.至某时刻t'(对应于图中x轴上、下两块面积相等)它回到A板小孔,并冲出小孔,脱离电场,C不正确. 指向A板的电场力作用被挡在A板小孔处.在T以后的时间内,它的达动情况与在t=0时进入电场时一样,只会一直向着B板,交替作着加速、减速运动,不会时而向B板,时而向A板运动,D也错. [答] A、B正确. 【例3】 从阴极K发射的电子经电势差U0=5000V的阳极加速后,沿平行于板面的方向从中央射入两块长L1 =10cm、间距d=4cm的平行金属板A、B之间,在离金属板边缘L2=75cm处放置一个直径D=20cm、带有记录纸的圆筒.整个装置放在真空内,电子发射的初速度不计(图1). 若在两金属板上加以U2=1000cos2πtV的交变电压,并使圆筒绕中心轴按图示方向以n=2转/s匀速转动,确定电子在记录纸上的轨迹形状并画出1s内所记录到的图形. [分析] 电子被加速后进入偏转电场.由于板上的电压和板间场强都作周期性变化,使得电子的偏距也作周期性变化. [解] 由电场力做功与动能变化的关系 得电子加速后的入射速度 加上交变电压时,A、B两板间场强 电子飞离金属板时的偏距 电子飞离金属板时的竖直速度 电子从飞离金属板到达圆筒时的偏距 所以在纸筒上的落点对入射方向的总偏距(见图2)为 可见,在记录纸上的点以振幅0.20m,周期 转1周),故在1s内,纸上的图形如图3所示. 【例4】 半径为r 的绝缘光滑圆环固定在竖直平面内,环上套有一质量为m、带正电的珠子,空间存在水平向右的匀强电场,如图所示.珠子所受静电力是其重力的3/4倍.将珠子从环上最低位置A点静止释放,则珠子所能获得的最大动能Ek=_____. [分析] 设珠子的带电量为q,电场强度为E.珠子在运动过程中 重力mg、竖直向下,环的弹力N、垂直圆环方向.其中只有电场力和重力能对珠子做功.其合力大小为 它与竖直方向间夹角为θ,(图2)则 珠子从A点释放后沿着圆环向右 运动,当它对初位置A的偏角小于θ时,合力F对珠子做正功,珠子的动能增大;当它对初始位置A的偏角大于θ时,合力F对珠子做负功,珠子的动能减小.可见,只有当珠子的偏角恰等于θ时,即其速度方向垂直F时,珠子的动能达最大值.由动能定理得珠子动能的最大值为 [说明] 水平方向的电场,相当于空间有一个水平力场,水平力场 度为 g'与g之间的夹角设为θ(图). 珠子沿圆环运动,可以类比于单摆的振动,运动中动能最大的位置就是当它与圆心的连线(相当摆长)沿着g'方向的位置(平衡位置).于是由能的转换立即可求出 【例5】 一根光滑的绝缘直杆与水平面成α=30°角倾斜放置,其BC部分在水平向右的匀强电场中,电场强度E=2×104N/C,在细杆m=3×10-2kg.今使小球从静止起沿杆下滑,从B点进入电场,如图,已知AB=s1=1m,试问 (1)小球进入电场后能滑行多远? (2)小球从A滑至最远处的时间是多少? [分析] 小球在AB部分滑行时,受到两个力作用:重力和杆的弹力.进入电场后又受到恒定的电场力FE(FE=Eq)的作用,其方向沿水平向左,它一方面增加了球对杆的压力,同时也形成一个沿杆向上的分力,将使小球作匀减速运动.B点就是上、下两段加速度发生方向变化的转折点.掌握了这个运动特点就可以推算出滑行距离和时间了. [解] (1)小球在AB段的加速度 a1=gsinα=10sin30°=5m/s2. 小球运动至B点的速度 进入电场后的加速度设为a2,则由 mgsinα-Eqcosα=ma2, 式中负号表示其方向沿CB向上. 设小球沿杆滑行至C点时的速度Vc=0,BC相距为s2,则由 (2)由上面的计算知,小球在AB段和BC段加速度的大小相等而方向相反.且在电场外和电场内滑行的距离相等,因此,小球从A滑至B的时间等于它从B滑至C的时间,所以小球A从滑至C的时间: [说明] 如果从A→C的全过程考虑:由 mgsinα(SAB+SBC)- Eqcosα·SBC= 0, 立即可得 SBC=s2=1m. 从A到C的运动时间,同样可从全过程考虑. 【例6】 在间距d=0.1m、电势差U=103V的两块竖立平行板中间,用一根长l=0.01m的细线悬挂一个质量m=0.2g、电量q=10-7C的带正电荷的小球,将小球拉到使丝线恰呈水平的位置A后轻轻释放如图,问: (1)小球摆至最低点B时的速度和线中的拉力多大? (2)若小球摆至B点时丝线突然断裂,以后小球恰能经过B点正下方的C点,则BC相距多远?(g=10m/s2) [分析] 小球带正电荷,在A点刚释放时,在水平向右的电场力和竖直向下的重力作用下,丝线立即被绷紧,此后小球在电场力、重力、丝线张力的作用下做变速圆周运动.在B点小球脱离后,水平方向仅受恒定的电场力作用,犹如“横向上抛”,竖直方向做自由落体运动. [解] (1)设小球摆至B点的速度为vB.由重力和电场力的合力做功得 在B点,根据圆运动的瞬时特性.由绳中张力和重力的合力作为向心力,即 又联立(1)~(3)三式,得 (2)在B点脱离后,小球在水平方向受到恒定的电场力作用,使小球产生水平向右的加速度, 因此,小球在水平方向做匀减速运动,犹如“横向上抛”,落回同一竖直线上的C点所需时间 小球在竖直方向仅受重力作用,脱离时竖直初速度为零,因此,小球在竖直方向做自由落体运动. [例7]一质量为m,带有电荷-q的小物体,可在水平轨道OX上运动,O端有一个与轨道垂直的固定墙。轨道处于匀强电场中,场强大小为E,方向沿Ox轴正方向,如图所示,小物体以初速v0从X0点沿OX轨道运动,运动时受到大小不变的摩擦力f作用,且f<qE,设小物体与墙碰撞时不损失机械能,且电量保持不变,求它在运动停止前所通过的总路程S。 [分析]小物体带负电,受到的电场力F=qE,方向与E方向相反,即沿X轴负方向,指向O点,摩擦力的方向总是跟小物体运动的方向相反,由于小物体初速度v0的方向未知,但只有两种可能,不是沿x轴正方向,就是沿X轴负方向,不论f的方向如何,因为f<qE,小物体沿x轴正方向运动总是做匀减速运动,沿X轴负方向总是做匀加速运动,在O点的右侧小物体所受的合外力不可能为零,只有在O 点处所受合外力(除F和f外还有墙对小物体的弹力)才有可能等于零。因此小物体最后只能停止在O点。 小物体停止时,它所具有动能消耗在克服摩擦力做功上,同时由于电场力做的功跟路径无关,只决定于始末位置,因此本题可用动能定理求解。 [解]设小物体往复运动至停止运动时通过的总路程为s根据动能定理。 [说明]本题的疑难点有二,一是小物体最终会停在何处。这个疑点,只能从平衡条件,(F合=0)去考虑,二是小物体与墙碰撞几次无法确定,由于所求的是总路程,而克服摩擦力做的功跟总路程有关。由此出发可以求解总路程S。 本题用牛顿运动定律和运动学公式无法求解,由于以上两个难题无法解决。但运用动能定理,只考虑始末状态,而不必考虑过程的细节,只要找到小物体最后停止运动的位置,问题就迎刃而解。查看更多