2019届二轮复习第23讲 不等式选讲(选修4-5)学案(全国通用)
第 23 讲 不等式选讲(选修 4-5)
考 情 分 析 【p87】
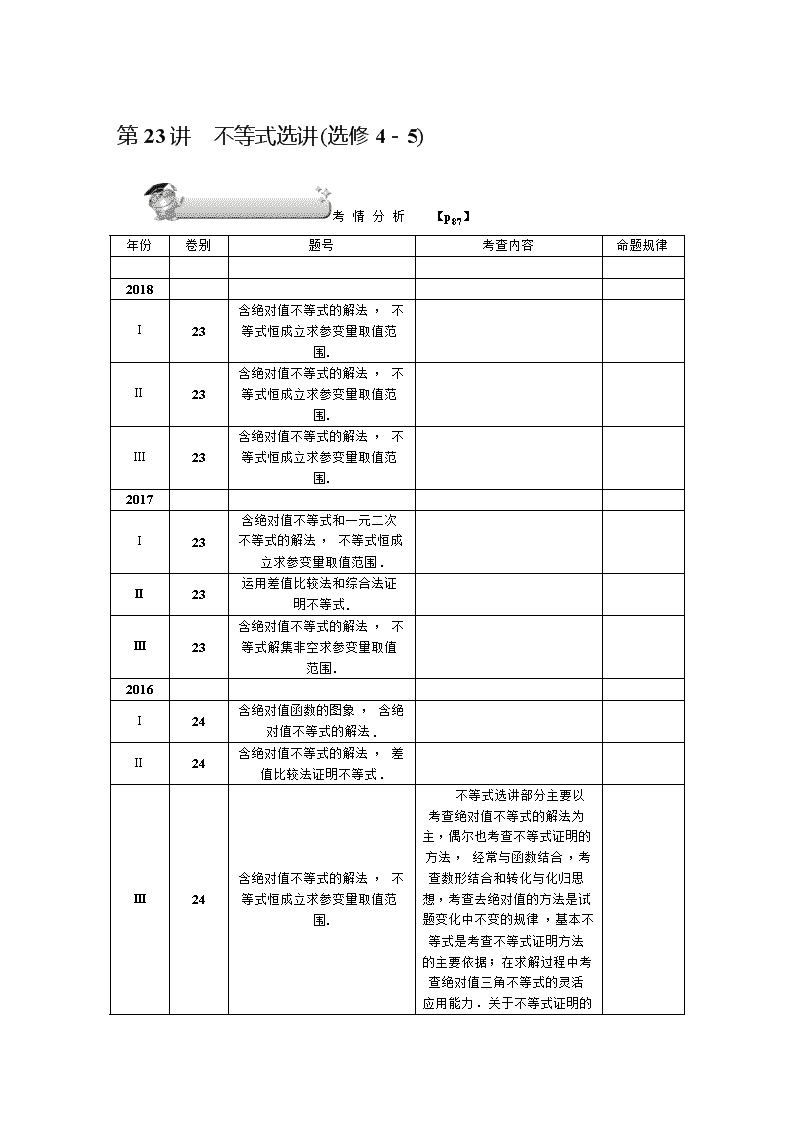
年份 卷别 题号 考查内容 命题规律
2018
Ⅰ 23
含绝对值不等式的解法, 不
等式恒成立求参变量取值范
围.
Ⅱ 23
含绝对值不等式的解法, 不
等式恒成立求参变量取值范
围.
Ⅲ 23
含绝对值不等式的解法, 不
等式恒成立求参变量取值范
围.
2017
Ⅰ 23
含绝对值不等式和一元二次
不等式的解法, 不等式恒成
立求参变量取值范围.
Ⅱ 23
运用差值比较法和综合法证
明不等式.
Ⅲ 23
含绝对值不等式的解法, 不
等式解集非空求参变量取值
范围.
2016
Ⅰ 24
含绝对值函数的图象, 含绝
对值不等式的解法.
Ⅱ 24
含绝对值不等式的解法, 差
值比较法证明不等式.
Ⅲ 24
含绝对值不等式的解法, 不
等式恒成立求参变量取值范
围.
不等式选讲部分主要以
考查绝对值不等式的解法为
主,偶尔也考查不等式证明的
方法, 经常与函数结合,考
查数形结合和转化与化归思
想,考查去绝对值的方法是试
题变化中不变的规律,基本不
等式是考查不等式证明方法
的主要依据;在求解过程中考
查绝对值三角不等式的灵活
应用能力.关于不等式证明的
方法,只有方法要求,因此它
的载体丰富多彩.
专 题 探 究 【p87】
【命题趋势】
从近几年的高考命题看,对本专题的考查主要体现在不等式的解法,利用几个重要的不等式
求函数的最值以及不等式的证明,全国高考以选考试题的形式出现,只有解答题,难度不大.考
查学生的基本运算能力及推理论证能力.
预计在今年高考中,对不等式选讲的考查主要有不含有绝对值的不等式的解法、含有绝对值
的函数的值域或求参数问题,用比较法、分析法、综合法证明简单不等式,全国高考试题仍然还
是以选考试题的形式出现,分值为 10 分,难度中等偏下.
【备考建议】
1.复习含有绝对值不等式时,既要掌握含绝对值不等式的解法及去绝对值的基本思想,又要
理解绝对值的几何意义,并能应用(1)|a+b|≤|a|+|b|;(2)|a-b|≤|a-c|+|c-b|证明不等式或求最
值.
2.复习不等式的证明时,要求学生了解和掌握不等式的常用证明方法:比较法、综合法、分
析法、反证法、放缩法等.
典 例 剖 析 【p87】
探究一 绝对值不等式的解法与恒成立问题
例 1 已知函数 f(x)=|2x-1|+|x-2a|.
(1)当 a=1 时,求 f(x)≤3 的解集;
(2)当 x∈[1,2]时,f(x)≤3 恒成立,求实数 a 的取值范围.
【解析】(1)当 a=1 时,由 f(x)≤3,可得|2x-1|+|x-2|≤3,
∴①{x <
1
2,
1-2x+2-x ≤ 3
或②{1
2 ≤ x < 2,
2x-1+2-x ≤ 3,
或③{x ≥ 2,
2x-1+x-2 ≤ 3.
解①得 0≤x<
1
2,解②得1
2≤x<2,解③得 x=2.
综上可得,0≤x≤2,即不等式的解集为[0,2],
(2)∵当 x∈[1,2]时,f(x)≤3 恒成立,
即|x-2a|≤3-|2x-1|=4-2x,
故 2x-4≤2a-x≤4-2x,
即 3x-4≤2a≤4-x.
再根据 3x-4 在 x∈[1,2]上的最大值为 6-4=2,4-x 的最小值为 4-2=2,
∴2a=2,∴a=1,
即 a 的取值范围为{1}.
例 2 已知函数 f(x)=-x2+ax+4,g(x )=|x+1 |+|x-1 |.
(1)当 a=1 时,求不等式 f(x)≥g(x)的解集;
(2)若不等式 f(x)≥g(x)的解集包含[-1,1],求 a 的取值范围.
【解析】(1)当 a=1 时,f(x )=-x2+x+4,是开口向下,对称轴 x=1
2的二次函数.
g(x )=|x+1 |+|x-1 |={2x ,x > 1,
2 , -1 ≤ x ≤ 1,
-2x ,x < -1,
当 x∈(1,+∞)时,令-x2+x+4=2x
,解得 x= 17-1
2 ,g (x )在(1 , +∞)上单调递增,f (x )在(1 , +∞)上单调递减,∴
此时 f(x )≥g (x )解集为(1 ,
17-1
2 ].
当 x∈[-1 ,1]时,g(x )=2,f(x )≥f(-1 )=2.
当 x∈(-∞ , -1)时,g (x )单调递减,f (x )单调递增,且 g(-1 )=f(-1 )=2.
综上所述,f(x )≥g (x )的解集为[-1 ,
17-1
2 ].
(2)依题意得:-x2+ax+4≥2 在[-1 ,1]恒成立.即 x2-ax-2≤0 在[-1 ,1]恒成立.
则只须{12-a·1-2 ≤ 0,
(-1 )
2
-a(-1 )-2 ≤ 0,解出:-1≤a≤1.故 a 取值范围是[-1 ,1].
【点评】1.形如|x-a|+|x-b|≥c(或≤c)型的不等式主要有两种解法:
(1)分段讨论法:利用绝对值号内式子对应方程的根,将数轴分为(-∞,a],(a,b],(b,+∞)
(此处设 a
1 的解集;
(2)若 x∈(0,1 )时不等式 f(x )>x 成立,求 a 的取值范围.
【解析】(1)依题意,|x+1 |-|x-1 |>1,
该不等式等价于{x < -1,
-x-1+x-1 > 1,
{-1 ≤ x ≤ 1,
x+1+x-1 > 1,或{x > 1,
x+1-x+1 > 1,
解得 x>
1
2,即不等式 f(x )>1 的解集为{x|x >
1
2 };
(2)依题意,|x+1 |-|ax-1|>x;当 x∈(0,1 )时,该式化为 x+1-|ax-1|>x,即|ax-1|<1,
即-1 0,
ax < 2 在(0,1 )上恒成立,
故 00,b>0,a3+b3=2,证明:
(1)(a+b)(a5+b5)≥4;
(2)a+b≤2.
【解析】(1)解法一:由柯西不等式得:
(a+b)(a5+b5)=[( a)2+( b)2]·[( a·a2)2+( b·b2)2]≥(a3+b3)2=4.
解法二:(a+b)(a5+b5)=a6+b6+ab5+a5b=(a3+b3)2+ab5+a5b-2a3b3
≥(a3+b3)2+2 a6b6-2a3b3=(a3+b3)2=4.
解法三:(a+b )(a5+b5)-4=(a+b )(a5+b5)-(a3+b3)2
=ab5+a5b-2a3b3,
又 a>0,b>0,所以 ab5+a5b-2a3b3=ab(a2-b2)2
≥0.当 a=b 时,等号成立.
所以,(a+b )(a5+b5)-4≥0,即(a+b)(a5+b5)≥4.
(2)解法一:由 a3+b3=2 及 ab≤
(a+b)2
4 得
2=(a+b)·(a2+b2-ab)=(a+b)·[(a+b)2-3ab]≥
(a+b)·[(a+b)2-3(a+b)2
4 ]
=
(a+b)3
4 .
所以 a+b≤2.
解法二:(反证法)假设 a+b>2,则 a>2-b,两边同时立方得:a3>(2-b)3=8-12b+6b2-b3,
即 a3+b3>8-12b+6b2,因为 a3+b3=2,
所以 6-12b+6b2<0,即 6(b-1)2<0,矛盾,所以假设不成立,即 a+b≤2.
解法三:因为 a3+b3=2,
所以(a+b )
3
-8=(a+b )
3
-4(a3+b3)=a3+3a2b+3ab2+b3-4a3-4b3
=3a2(b-a )+3b2(a-b )=-3(a+b )(a-b )
2
.
又 a>0,b>0,所以-3(a+b )(a-b )
2
≤0,
所以(a+b )
3
≤8,即 a+b≤2.
解法四:因为 a3+1+1≥33 a3=3a,b3+1+1≥33 b3=3b,所以 a3+1+1+b3+1+1≥3(a+b)
,即 6≥3(a+b),即 a+b≤2(当且仅当 a=b=1 时取等号).
【命题立意】本题主要考查不等式证明方法的应用能力和推理论证能力.
考点限时训练 【p158】
A 组 基础演练
1.已知函数 f(x)=|2x+1|+|2x-3|.
(1)求不等式 f(x)≤6 的解集;
(2)若关于 x 的不等式 f(x)<|a-1|的解集不是空集,求实数 a 的取值范围.
【解析】(1)原不等式等价于
{x >
3
2,
(2x+1)+(2x-3) ≤ 6
或{-1
2 ≤ x ≤ 3
2,
(2x+1)-(2x-3) ≤ 6
或
{x < -1
2,
-(2x+1)-(2x-3) ≤ 6,
解得3
24,∴a<-3 或 a>5,
∴实数 a 的取值范围为(-∞,-3)∪(5,+∞).
2.已知函数 f(x)=|x+a|+|x-2|.
(1)当 a=-3 时,求不等式 f(x)≥3 的解集;
(2)若 f(x)≤|x-4|的解集包含[1,2],求 a 的取值范围.
【解析】(1)当 a=-3 时,
不等式 f(x)≥3 化为|x-3|+|x-2|≥3.①
若 x≤2 时,由①式,得 5-2x≥3,∴x≤1.
若 2
1
2,
所以 φ (n )的最小值为 4,故实数 m 的取值范围是[4,+∞).
6.设函数 f(x)=|x-3|-|x+1|,x∈R.
(1)解不等式 f(x)<-1;
(2)设函数 g(x)=|x+a|-4,且 g(x)≤f(x)在 x∈[-2,2]上恒成立,求实数 a 的取值范围.
【解析】(1)函数 f(x)=|x-3|-|x+1|={4,x < -1,
2-2x,-1 ≤ x ≤ 3,
-4,x > 3,
故由不等式 f(x)<-1 可得,x>3 或{2-2x < -1,
-1 ≤ x ≤ 3.
解得 x>
3
2.
(2)函数 g(x)≤f(x)在 x∈[-2,2]上恒成立,
即|x+a|-4≤|x-3|-|x+1|在 x∈[-2,2]上恒成立,
在同一个坐标系中画出函数 f(x)和 g(x)的图象,如图所示.
故当 x∈[-2,2]时,若 0≤-a≤4,则函数 g(x)的图象在函数 f(x)的图象的下方,g(x)≤f(x)
在 x∈[-2,2]上恒成立,求得-4≤a≤0,
故所求的实数 a 的取值范围为[-4,0].
7.已知 a>0,b>0,a+b=1,求证:
(1)
1
a+1
b+ 1
ab≥8;
(2)(1+1
a )(1+1
b )≥9.
【解析】证明:(1)∵a+b=1,a>0,b>0,
∴1
a+1
b+ 1
ab=1
a+1
b+a+b
ab
=2(1
a
+1
b )=2(a+b
a
+a+b
b )
=2(b
a
+a
b )+4
≥4
b
a·
a
b+4=8(当且仅当 a=b=1
2时,等号成立),
∴1
a+1
b+ 1
ab≥8.
(2)∵(1+1
a )(1+1
b )
=1
a+1
b+ 1
ab+1,
由(1)知1
a+1
b+ 1
ab≥8.
∴(1+1
a )(1+1
b )≥9.
B 组 能力提升
8.已知函数 f(x)=m-|x-1|-|x-2|,m∈R,且 f(x+1)≥0 的解集为[0,1].
(1)求 m 的值;
(2)若 a,b,c,x,y,z∈R,且 x2+y2+z2=a2+b2+c2=m,求证:ax+by+cz≤1.
【解析】(1)由 f(x+1)≥0 得|x|+|x-1|≤m.
∵|x|+|x-1|≥1 恒成立,
∴若 m<1,不等式|x|+|x-1|≤m 的解集为∅,不合题意.
若 m≥1,①当 x<0 时,得 x≥1-m
2 ,则1-m
2 ≤x<0;
②当 0≤x≤1 时,得 x+1-x≤m,即 m≥1 恒成立;
③当 x>1 时,得 x≤m+1
2 ,则 11,|y|<1,求证:f(y)<|x|·f( y
x2 ).
【解析】(1)原不等式即为|x+9 |≥10-|x+1 |.
当 x<-9 时,则-x-9≥10+x+1,解得 x≤-10;
当-9≤x≤-1 时,则 x+9≥10+x+1,此时不成立;
当 x>-1 时,则 x+9≥10-x-1,解得 x≥0.
所以原不等式的解集为{x|x≤-10 或 x≥0}.
(2)要证 f(y )<|x |·f( y
x2 ),
即|y+1 |<|x |·| y
x2+1 |,
只需证明|y+1 |
|x |<| y
x2+1 |.
则有
(y+1 )
2
x2 -
(y+x2 )
2
x4 =
x2(y+1 )2
-(y+x2 )
2
x4
=x2y2+2x2y+x2-(y2+2x2y+x4)
x4
=x2y2+x2-y2-x4
x4
=(1-x2 )(x2-y2)
x4 .
因为|x|2>1,|y|2<1,
则
(y+1 )
2
x2 -
(y+x2 )
2
x4 =(1-x2 )(x2-y2)
x4 <0,
所以
(y+1 )
2
x2 <
(y+x2 )
2
x4 ,原不等式得证.
11.已知函数 f(x)=|x+1|.
(1)求不等式 f(x)<|2x+1|-1 的解集 M;
(2)设 a,b∈M,证明:f(ab)>f(a)-f(-b).
【解析】(1)解:①当 x≤-1 时,原不等式可化为-x-1<-2x-2,解得 x<-1;
②当-11.
综上,M={x|x<-1 或 x>1}.
(2)证明:∵f(a)-f(-b)=|a+1|-|-b+1|≤|a+1-(-b+1)|=|a+b|,
∴要证 f(ab)>f(a)-f(-b),
只需证|ab+1|>|a+b|,即证|ab+1|2>|a+b|2,
即证 a2b2+2ab+1>a2+2ab+b2,
即证 a2b2-a2-b2+1>0,即证(a2-1)(b2-1)>0.
∵a,b∈M,∴a2>1,b2>1.
∴(a2-1)(b2-1)>0 成立,∴原不等式成立.