- 2021-04-13 发布 |
- 37.5 KB |
- 9页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
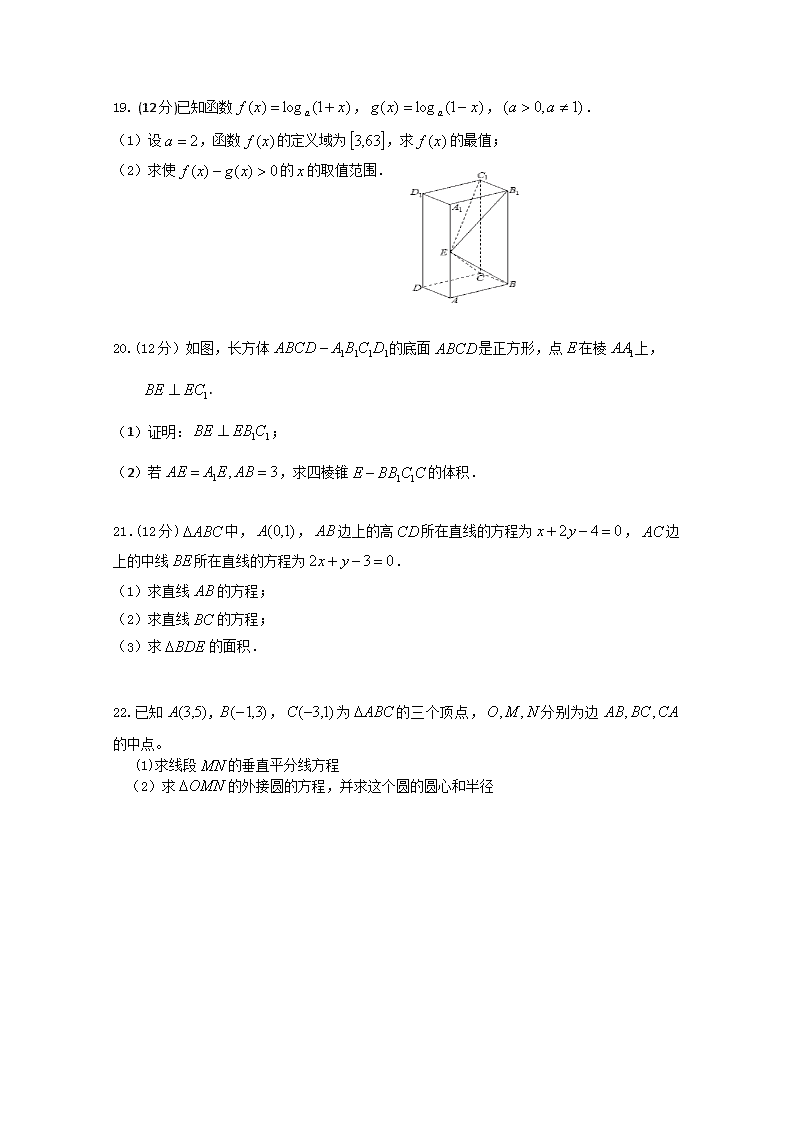
黑龙江省大兴安岭漠河县第一中学2019-2020学年高一期末考试数学试卷
www.ks5u.com 数学试题 一、选择题(本大题共12个小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的) 1.已知集合,,则=( ) A. B. C. D. 2.下列各函数中,值域为的是( ) A. B. C. D. 3. 过点且与直线平行的直线方程为( ) A. B. C. D. 4. 函数,若,则的值是( ) A. B. C.或 D.或 5.已知幂函数的图象经过点,则的值为( ) A. B. C. D. 6.圆心为且过原点的圆的方程是( ) A. B. C. D. 7. 方程的解所在的区间是( ) A. B. C. D. 8.直线关于直线对称的直线方程是( ) A. B. C.D. 9.设是两个不同的平面,是两条不同的直线,给出下列四个论断①;②③;④.以其中三个论断作为条件,余下一个论断作为结论,则一共可以写出真命题的个数为( ) A.1 B.2 C.3 D.4 10.已知直线,则当变化时,所有直线都通过定点( ) A. B. C. D. 11.在正方体中,为棱的中点,则异面直线与所成角的正切值为 A. B. C. D. 12.设,,则的最小值和最大值分别为( ) A., B. C., D., 二.填空题(本大题共4道小题,每道小题5分,满分20分.) 13.已知集合,且,则实数的取值范围是 . 14.已知,则________. 15.经过点且横、纵截距相等的直线方程是____________________ 16.点在轴上运动,点在直线:上运动,若,则的周长的最小值为 三.解答题(本大题共6道小题,满分70分,解答应写出文字说明,证明过程或演算步骤.) 17.(10分)已知直线经过点且斜率为, (1)求直线的方程; (2)若直线平行于直线,且点到直线的距离为,求直线的方程 18. (12分)如图,在直三棱柱中,分别为的中点,. 求证:(1)平面; (2). 19. (12分)已知函数,,. (1)设,函数的定义域为,求的最值; (2)求使的的取值范围. 20.(12分)如图,长方体的底面是正方形,点在棱上,. (1)证明:; (2)若,求四棱锥的体积. 21.(12分)中,,边上的高所在直线的方程为,边上的中线所在直线的方程为. (1)求直线的方程; (2)求直线的方程; (3)求的面积. 22.已知,,为的三个顶点,分别为边的中点。 (1)求线段的垂直平分线方程 (2)求的外接圆的方程,并求这个圆的圆心和半径 数学试题 答案: 1.【解答】解:∵集合A={1,2,3,4}, B={x|﹣2≤3x﹣2≤10,x∈R}={x|0≤x≤4},∴A∩B={1,2,3,4}.故选:B. 2.【解析】A,的值域为. B,因为,所以,,的定义域是, 所以,所以,所以的值域是. C,的值域是, D,因为, 所以的值域是.故选A 3. 【解答】解:设过点(﹣1,3)且与直线x﹣2y+3=0平行的直线方程为 x﹣2y+m=0,把点(﹣1,3)代入直线方程得﹣1﹣2×3+m=0,m=7,故所求的直线方程为x﹣2y+7=0,故选A. 4.【解答】解:若a<2,则由f(a)=1得,3a﹣2=1,即a﹣2=0,∴a=2.此时不成立.若a≥2,则由f(a)=1得,log=1,得a2﹣1=3,即a2=4,∴a=2, 故选:A. 5.【解答】解:设幂函数为y=xα, ∵幂函数y=f(x)的图象经过点(2,),∴=2α,解得α=.y=x. f(4)==.故选:C. 6.【解答】解:由题意可知,圆的半径为r=. ∴圆心为(1,2)且过原点的圆的方程是(x﹣1)2+(y﹣2)2=5.故选:C 7.【答案】C 【解析】令f(x)=2x-1+x-5,则f(2)=2+2-5=-1<0,f(3)=22+3-5=2>0, 从而方程在区间(2,3)内有解.故选C. 8. 【答案】D 【解析】将“关于直线对称的两条直线”转化为“关于直线对称的两点”:在直线x-2y+1=0上取一点P(3,2),点P关于直线x=1的对称点P′(-1,2)必在所求直线上,故选D. 9.【解答】:同垂直于一个平面的两条直线互相平行,同垂直于两个平行平面的两条直线也互相平行.故②③④⇒① 同理,①②③⇒④,①②④⇒③,①③④⇒②为真命题 故选D 10.【解答】C 直线方程变形为k(3x+y-1)+(2y-x)=0,则直线通过定点(,).故选C. 11.【解答】C【解析】如图,连接,因为,所以异面直线与所成角等于相交直线与所成的角,即.不妨设正方体的棱长为2,则,,由勾股定理得,又由平面,可得, 所以,故选C. 12.【答案】A 【解析】x2+y2为线段AB上的点与原点的距离的平方,由数形结合知, O到线段AB的距离的平方为最小值,即d2=,|OB|2=1为最大值.故选A. 二.填空题(本大题共4道小题,每道小题5分,满分20分.) 13.已知集合A={x|x2﹣2x+a>0},且1∉A,则实数a的取值范围是 (﹣∞,1] . 【解答】解:根据1∉ A,可知,集合A在实数集当中没有元素1,又集合A中的元素是由一元二次不等式构成的解集, 故问题可转化为一元二次不等式没有实数1.由12﹣2+a≤0 解得 a≤1. 故答案为:(﹣∞,1]. 14.【答案】4 【解析】∵,∴,即,∴ 15.【解答】答案】或x+y+3=0 【解析】不能忽略直线过原点的情况 16.【解答】解:A关于y轴的对称点M,A关于l:x﹣y﹣2=0的对称点D, ∴MB=BA,AC=CD连接MD交直线l:x﹣y﹣2=0与C,交y轴于B, 则此时△ABC的周长的值最小,即DM的长度即为三角形周长的最小值, 由题意及作图知M(-2,3).D(5,0) 由两点距离公式知,DM=. 故答案为. 17.【答案】(1)3x+4y-14=0;(2)3x+4y+1=0或3x+4y-29=0. (1)直线l的方程为:y-5=-(x+2)整理得3x+4y-14=0. (2)设直线m的方程为3x+4y+n=0, d==3,解得n=1或-29. ∴直线m的方程为3x+4y+1=0或3x+4y-29=0. 18.【解答】(1)因为D,E分别为BC,AC的中点, 所以ED∥AB. 在直三棱柱ABC-A1B1C1中,AB∥A1B1, 所以A1B1∥ED. 又因为ED⊂平面DEC1,A1B1平面DEC1, 所以A1B1∥平面DEC1. (2)因为AB=BC,E为AC的中点,所以BE⊥AC. 因为三棱柱ABC-A1B1C1是直棱柱,所以CC1⊥平面ABC. 又因为BE⊂平面ABC,所以CC1⊥BE. 因为C1C⊂平面A1ACC1,AC⊂平面A1ACC1,C1C∩AC=C, 所以BE⊥平面A1ACC1. 因为C1E⊂平面A1ACC1,所以BE⊥C1E. 19.【答案】(1)最小值为2,最大值为6;(2)见解析. 【解析】(1)当a=2时,f(x)=log2(1+x),在[3,63]上为增函数, 因此当x=3时,f(x)最小值为2.当x=63时f(x)最大值为6. (2)f(x)-g(x)>0即f(x)>g(x) 当a>1时,loga(1+x)>loga(1-x),满足∴0<x<1 当0<a<1时,loga(1+x)>loga(1-x),满足∴-1查看更多
相关文章
- 当前文档收益归属上传用户
- 下载本文档