中考数学二轮精品练习：全等三角形

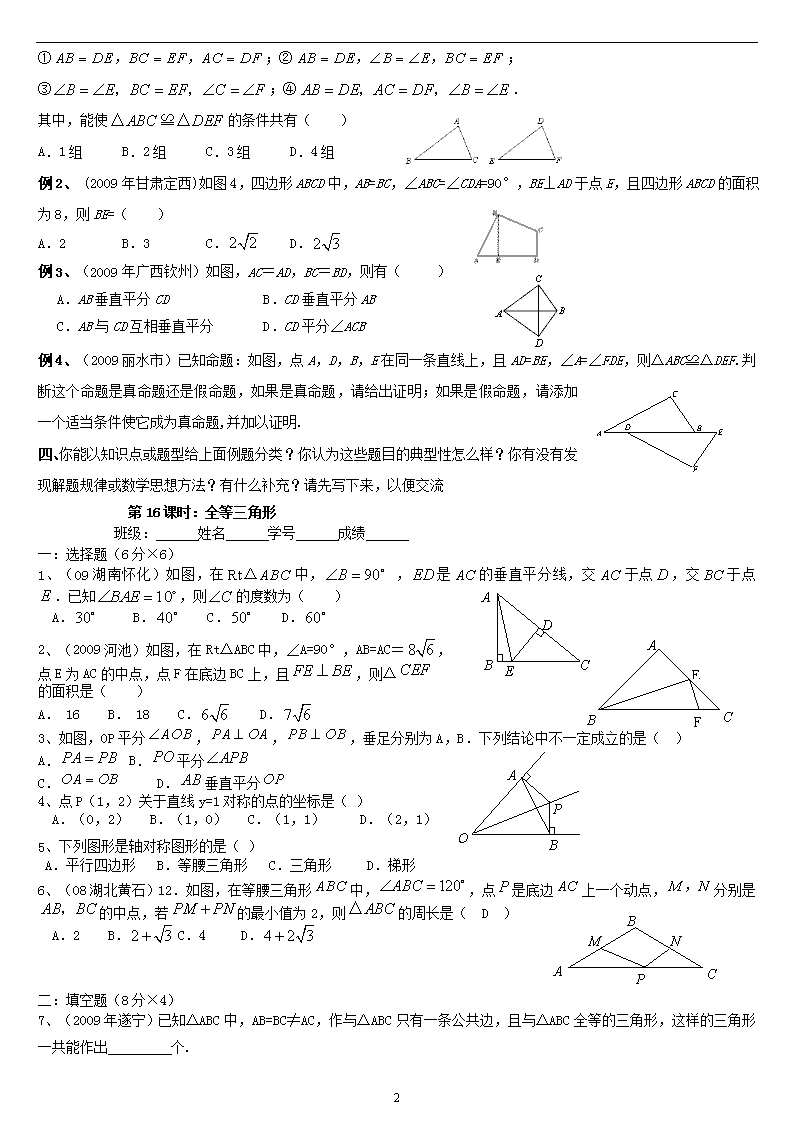
中考数学二轮精品练习：全等三角形

‎ ‎ 全等三角形 A B C D E 一、下列各题已有解答的有“病”吗？如果有“病”，请写出“病因”。没有解答的，你认为易让别人犯错的“陷阱”在哪儿？‎ ‎1．已知△ABD≌△ACE，求证：△ABE≌△ACD ‎ 证明：∵△ABD≌△ACE ‎∴△ABD+△ADE≌△ACE+△ADE ∴△ABE≌△ACD ‎▲错因分析或陷阱是 ‎ ‎▲正确解答是： ‎ A B C O ‎1‎ ‎2‎ ‎ ‎ ‎2．如图，AO平分∠BAC，∠1=∠2 求证：△ABC是等腰三角形 证明：∵∠1=∠2 ∴ OB=OC ‎ ∵AO平分∠BAC ∴∠BAO=∠CAO ‎ 在△AOB≌△AOC中∵OB=OC 、∠BAO=∠CAO 、OA=OA ‎ ∴△AOB≌△AOC ∴AB=AC ，即△ABC是等腰三角形 ‎▲错因分析或陷阱是 ‎ ‎▲正确解答是： ‎ ‎ ‎ ‎3．两边和第三边上的高对应相等相等的两个三角形全等(判断)‎ ‎ 解：通过两次全等，可以证明这个命题是正确的 ‎▲错因分析或陷阱是_____________________________________________________ ‎ ‎▲正确解答是___________________________________________________________‎ 二、“全等三角形”给你留下多少？尝试填写下列知识点（并在脑海中构建知识体系）‎ ‎1、 叫全等三角形 ‎2、全等三角形的性质：全等三角形的对应边 、全等三角形的对应角 、‎ 全等三角形的对应边上的高 、全等三角形的对应边上的中线 、全等三角形的对应角的平分线 ‎ ‎3、三角形全等的判定方法：‎ ‎（1） 的两个三角形全等（简记为 SSS ）‎ ‎（2） 的两个三角形全等（简记为 SAS ）‎ ‎（3） 的两个三角形全等（简记为 ASA ）‎ ‎（4） 的两个三角形全等（简记为 AAS ）‎ ‎（5） 的两个三角形全等（简记为 HL ）‎ ‎4、满足下面的条件的两个三角形也是全等的：‎ ‎（1）有两边和其中一边上的中线对应相等的两个三角形全等 （2）有两边和第三边上的中线对应相等的两个三角形全等（3）有两角和其中一个角的平分线对应相等的两个三角形全等（4）有两角和第三个角的平分线对应相等的两个三角形全等（5）有两边和其中一边上的高对应相等的两个锐角（或钝角）三角形全等（6）有两边和第三条边上的高对应相等的两个锐角（或钝角）三角形全等 ‎5、角平分线的性质 ‎ ‎6、角平分线的判定 ‎ ‎7、线段垂直平分线的性质 ‎ ‎8、线段垂直平分线的判定 ‎ ‎9、 叫轴对称图形 ‎ ‎10、 那么就说这两个图形关于这条直线对称 ‎11、用坐标表示轴对称：（1）点（x, y）关于x轴对称的点的坐标为 （2）点（x, y）关于y轴对称的点的坐标为 (3) 点（x, y）关于原点对称的点的坐标为 ‎ ‎ （4）点（x, y）关于直线x=m对称的点的坐标为 （5）点（x, y）关于直线y=m对称的点的坐标为 ‎ 三、下列例题请先做做，看自己有无“漏洞”如果有请偿试写出“病因”‎ 例1．（2009年江苏省）如图，给出下列四组条件：‎ 3‎ ‎ ‎ ‎①；②；‎ ‎③；④．‎ 其中，能使的条件共有（ ）‎ A．1组 B．2组 C．3组 D．4组 ‎ 例2、 (2009年甘肃定西)如图4，四边形ABCD中，AB=BC，∠ABC=∠CDA=90°，BE⊥AD于点E，且四边形ABCD的面积为8，则BE=（　　）‎ A．2 B．3 C． D．‎ 例3、（2009年广西钦州）如图，AC＝AD，BC＝BD，则有（ ）‎ ‎ A．AB垂直平分CD B．CD垂直平分AB ‎ C．AB与CD互相垂直平分 D．CD平分∠ACB 例4、（2009丽水市）已知命题：如图，点A，D，B，E在同一条直线上，且AD=BE，∠A=∠FDE，则△ABC≌△DEF.判断这个命题是真命题还是假命题，如果是真命题，请给出证明；如果是假命题，请添加一个适当条件使它成为真命题,并加以证明.‎ 四、你能以知识点或题型给上面例题分类？你认为这些题目的典型性怎么样？你有没有发现解题规律或数学思想方法？有什么补充？请先写下来，以便交流 第16课时：全等三角形 ‎ ‎ 班级： 姓名 学号 成绩 ‎ 一：选择题（6分×6）‎ A D C E B ‎1、（09湖南怀化）如图，在中， ，是的垂直平分线，交于点，交于点．已知，则的度数为（ ）‎ C B F A E A． B． C． D．‎ ‎2、（2009河池）如图，在Rt△ABC中，∠A=90°，AB=AC＝，‎ 点E为AC的中点，点F在底边BC上，且，则△‎ 的面积是（ ）‎ A． 16 B． 18 C． D．‎ ‎3、如图，OP平分，，，垂足分别为A，B．下列结论中不一定成立的是（ ）‎ O B A P A． B．平分 ‎ C． D．垂直平分 ‎4、点P（1，2）关于直线y=1对称的点的坐标是（ ）‎ A．（0，2） B．（1，0） C．（1，1） D．（2，1）‎ ‎5、下列图形是轴对称图形的是（ ）‎ ‎ A．平行四边形 B．等腰三角形 C．三角形 D．梯形 A B C P M N ‎6、（08湖北黄石）12．如图，在等腰三角形中，，点是底边上一个动点， 分别是的中点，若的最小值为2，则的周长是（ D ）‎ A．2 B． C．4 D． ‎ 二：填空题（8分×4）‎ ‎7、（2009年遂宁）已知△ABC中，AB=BC≠AC，作与△ABC只有一条公共边，且与△ABC全等的三角形，这样的三角形一共能作出 个.‎ 3‎ ‎ ‎ ‎8、(2009年福建省泉州市)如图，在△ABC中，BC边上的垂直平分线DE交边BC于点D，交边AB于点E.若△EDC的周长为24，△ABC与四边形AEDC的周长之差为12，则线段DE的长 ‎ ‎9、（2009河池）某小区有一块等腰三角形的草地，它的一边长为，面积为，为美化小区环境，现要给这块三角形草地围上白色的低矮栅栏，则需要栅栏的长度为　　　 _________m．‎ ‎10、、(2009年咸宁市)如图，在中，和的平分线相交于点，过点作交于，交于，过点作于．下列四个结论：‎ A D F C Ｂ Ｏ Ｅ ‎；‎ ‎②以为圆心、为半径的圆与以为圆心、为半径的圆外切；‎ ‎③设则；‎ ‎④不能成为的中位线．‎ 其中正确的结论是_____________．（把你认为正确结论的序号都填上）‎ 三：解答题（11题10分，12题10分，13题12分）‎ ‎11、（2009年浙江省绍兴市）如图，在中，，分别以 为边作两个等腰直角三角形和，使．‎ ‎（1）求的度数；‎ ‎（2）求证：． ‎ ‎12、(2009年安顺)如图，在△ABC中，D是BC边上的一点，E是AD的中点，过A点作BC的平行线交CE的延长线于点F，且AF=BD，连结BF。‎ ‎(1)求证：BD=CD；‎ ‎(2)如果AB=AC，试判断四边形AFBD的形状，并证明你的结论。 ‎ ‎13、（2009东营）已知正方形ABCD中，E为对角线BD上一点，过E点作EF⊥BD交BC于F，连接DF，G为DF中点，连接EG，CG．‎ ‎（1）求证：EG=CG；‎ ‎（2）将图①中△BEF绕B点逆时针旋转45º，如图②所示，取DF中点G，连接EG，CG．问（1）中的结论是否仍然成立？若成立，请给出证明；若不成立，请说明理由． ‎ ‎（3）将图①中△BEF绕B点旋转任意角度，如图③所示，再连接相应的线段，问（1）中的结论是否仍然成立？通过观察你还能得出什么结论？（均不要求证明）‎ D F B A C E 图③‎ F B A D C E G 图②‎ F B A D C E G 图①‎ ‎ ‎ 3‎